2023-2024学年湖北省七年级下学期数学期中仿真模拟卷二
试卷更新日期:2024-04-14 类型:期中考试
一、精心选一选(本大题共8小题,每小题3分,满分24分.)
-
1. 在下列各组由运动项目的图标组成的图形中,能将其中一个图形只经过平移得到另一个图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 图中,∠1和∠2是对顶角的是( )A、
2. 图中,∠1和∠2是对顶角的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列各数中,是无理数的为( )A、 B、3.14 C、 D、﹣4. 如图,下列条件中,能判定直线a∥b的是( )
3. 下列各数中,是无理数的为( )A、 B、3.14 C、 D、﹣4. 如图,下列条件中,能判定直线a∥b的是( ) A、∠1=∠2 B、∠1=∠5 C、∠3=∠5 D、∠1+∠4=180°5. 数学老师在操场上建立了一个平面直角坐标系,小丽站在点 , 小刚站在点 , 小丽说她在第二象限,那么小刚在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 已知点Q的坐标为 ,点P的坐标为 ,若直线 轴,则点P的坐标为( )A、 B、 C、 D、7. 若与是同一个数两个不同的平方根,则为( )A、 B、3 C、 D、18. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点 , 第二次从点运动到点 , 第三次从点运动到点 , …,按这样的运动规律,第2023次从点运动到点后,此时点的坐标是( )
A、∠1=∠2 B、∠1=∠5 C、∠3=∠5 D、∠1+∠4=180°5. 数学老师在操场上建立了一个平面直角坐标系,小丽站在点 , 小刚站在点 , 小丽说她在第二象限,那么小刚在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 已知点Q的坐标为 ,点P的坐标为 ,若直线 轴,则点P的坐标为( )A、 B、 C、 D、7. 若与是同一个数两个不同的平方根,则为( )A、 B、3 C、 D、18. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点 , 第二次从点运动到点 , 第三次从点运动到点 , …,按这样的运动规律,第2023次从点运动到点后,此时点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、细心填一填(本大题共8小题,每小题3分,满分24分.)
-
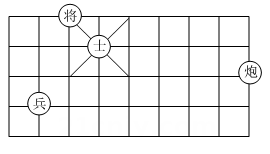
9. “平行于同一条直线的两条直线平行”是 命题(填“真”或“假”).10. 如图所示,若“兵”的位置是 , “炮”的位置是 , 则“将”的位置可以表示为 .
 11. 阅读下列材料:因为 , 即 , 所以的整数部分为2,小数部分为 , 若规定实数m的整数部分记为 , 小数部分记为 , 可得: , . 按照此规定计算的值 .12. 一个自然数的算术平方根是a,则相邻的下一个自然数的算术平方根是 .13. 有一个数值转换器,计算流程如图所示,当输入x的值为8时,输出的值是 .
11. 阅读下列材料:因为 , 即 , 所以的整数部分为2,小数部分为 , 若规定实数m的整数部分记为 , 小数部分记为 , 可得: , . 按照此规定计算的值 .12. 一个自然数的算术平方根是a,则相邻的下一个自然数的算术平方根是 .13. 有一个数值转换器,计算流程如图所示,当输入x的值为8时,输出的值是 .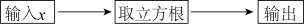 14. 如图,第一象限内有两点 , 将线段平移使点、分别落在两条坐标轴上,则点平移后的对应点的坐标是 .
14. 如图,第一象限内有两点 , 将线段平移使点、分别落在两条坐标轴上,则点平移后的对应点的坐标是 . 15. 如图为一盏可折叠台灯及其平面示意图,其中支架与底座垂直,支架 , 为固定支撑杆,当灯体与底座平行时, , , 则的度数为 .
15. 如图为一盏可折叠台灯及其平面示意图,其中支架与底座垂直,支架 , 为固定支撑杆,当灯体与底座平行时, , , 则的度数为 . 16. 如图,的角平分线、相交于F, , , 且于G.下列结论:①;②平分;③;④ . 其中正确的结论是 .
16. 如图,的角平分线、相交于F, , , 且于G.下列结论:①;②平分;③;④ . 其中正确的结论是 .
三、专心解一解(本大题共8小题,满分72分.)
-
17. 计算或求下列式子中的x:(1)、;(2)、;(3)、4x2=25;(4)、(x+1)3﹣8=0.18. 已知:如图,∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,且∠1=∠3.试说明:∠1+∠4=180°.
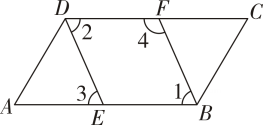
请将下列说理过程补充完整,并在括号内注明依据.
解:∵BF,DE分别平分∠ABC与∠ADC(已知),
( ) .
又∵∠ABC=∠ADC( ),
∴∠1=∠2(等量代换).
又∵∠1=∠3(已知),
∴∠2= ▲ ( ),
∴AB∥CD( ),
∴∠1+∠4=180°( )
19. 如图,直线 交于点O,已知 , .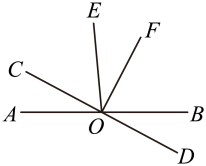 (1)、若 ,求 的度数;(2)、若 ,判断 与 的位置关系,并说明理由.20.(1)、实践与操作:如图,平移三角形 , 使点A平移到点 , 画出平移后的三角形(点B平移到 , 点C平移到);
(1)、若 ,求 的度数;(2)、若 ,判断 与 的位置关系,并说明理由.20.(1)、实践与操作:如图,平移三角形 , 使点A平移到点 , 画出平移后的三角形(点B平移到 , 点C平移到); (2)、猜想与推理:猜想'与的数量与位置关系 ▲ ,其依据是 ▲ .21. 已知某个正数的两个平方根分别是和 , 的立方根是2.(1)、求ab的值.(2)、求的平方根.22. 已知:如图,∠1=∠C,∠E=∠B.
(2)、猜想与推理:猜想'与的数量与位置关系 ▲ ,其依据是 ▲ .21. 已知某个正数的两个平方根分别是和 , 的立方根是2.(1)、求ab的值.(2)、求的平方根.22. 已知:如图,∠1=∠C,∠E=∠B.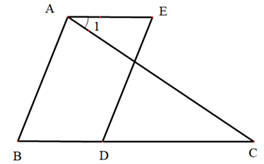 (1)、判断AB与DE的位置关系,并说明理由;(2)、若AB⊥AC于点A,∠1=36°,求∠BDE的度数.23. 如图,在平面直角坐标系xOy中,点A(a-1,a+2)位于第一象限,将点A向下平移一定单位长度得到点B(1,0),以AB为边在AB右侧作正方形ABCD.
(1)、判断AB与DE的位置关系,并说明理由;(2)、若AB⊥AC于点A,∠1=36°,求∠BDE的度数.23. 如图,在平面直角坐标系xOy中,点A(a-1,a+2)位于第一象限,将点A向下平移一定单位长度得到点B(1,0),以AB为边在AB右侧作正方形ABCD.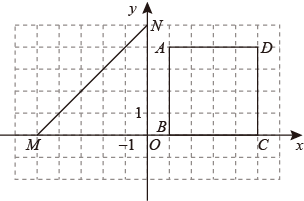 (1)、求a的值及点D的坐标;(2)、横、纵坐标都是整数的点叫做整点.已知点M(-5,0),N(0,5),将正方形ABCD向左平移m(m>0)个单位长度,得到正方形A′B′C′D′,记正方形A′B′C′D′ 和△OMN重叠的区域(不含边界)为W.
(1)、求a的值及点D的坐标;(2)、横、纵坐标都是整数的点叫做整点.已知点M(-5,0),N(0,5),将正方形ABCD向左平移m(m>0)个单位长度,得到正方形A′B′C′D′,记正方形A′B′C′D′ 和△OMN重叠的区域(不含边界)为W.① 当m=3时,区域W内的整点个数为 ▲ ;
② 若区域W内恰有3个整点,直接写出m的取值范围.
24. 综合与探究数学活动课上,老师以“一个含的直角三角板和两条平行线”为背景展开探究活动,

如图1,已知直线 , 直角三角板中, , .
(1)、如图1,若 , 则;(直接写出答案)(2)、“启航”小组在图1的基础上继续展开探究:如图 , 调整三角板的位置,当三角板的直角顶点在直线上,直线与 , 相交时,他们得出的结论是: , 你认为启航小组的结论是否正确,请说明理由;(3)、如图 , 受到“启航”小组的启发,“睿智”小组提出的问题是:在图的基础上,继续调整三角板的位置,当点不在直线上,直线与 , 相交时,与有怎样的数量关系?请你用平行线的知识说明理由.