2023-2024学年湖北省七年级下学期数学期中仿真模拟卷一
试卷更新日期:2024-04-14 类型:期中考试
一、选择题(共10小题,每小题3分,共30分)
-
1. 2023年9月23日至10月8日第十九届亚运动会将在中国杭州举办,其中吉祥物“莲莲”深受大家喜爱,在下列的四个图中能由如图所示的图形平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 在 , , , ,2023这五个数中无理数的个数为( )A、2 B、3 C、4 D、53. 在平面直角坐标系中,点P(﹣3,2)在 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图,直线AC和直线BD相交于点O,若∠1+∠2=70°,则∠BOC的度数是( ).
2. 在 , , , ,2023这五个数中无理数的个数为( )A、2 B、3 C、4 D、53. 在平面直角坐标系中,点P(﹣3,2)在 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图,直线AC和直线BD相交于点O,若∠1+∠2=70°,则∠BOC的度数是( ).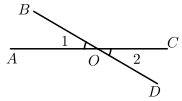 A、100° B、115° C、135° D、145°5. 下列图形中,根据∠1=∠2,能得到 AB∥CD 的是( )A、
A、100° B、115° C、135° D、145°5. 下列图形中,根据∠1=∠2,能得到 AB∥CD 的是( )A、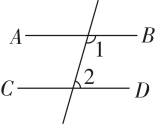 B、
B、 C、
C、 D、
D、 6. 下列说法正确的有( )
6. 下列说法正确的有( )①带根号的数都是无理数;
②立方根等于本身的数是和;
③一定没有平方根;
④实数与数轴上的点是一 一对应的;
⑤两个无理数的差还是无理数.
A、个 B、个 C、个 D、个7. 如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次平移,每次移动一个单位,得到点 , , , , …,那么点的坐标为( ) A、 B、 C、 D、8. 小明和小亮一起研究一道数学题,如图,BD⊥AC于点D,E是边BC 上的一点,过点 E作 EF⊥AC于点F,点G在AB上,连结DG,GE.小明说:“如果还知道∠GDB=∠FEC,则能得到∠AGD=∠ABC.”小亮说:“如果∠AGD=∠ABC,可得到∠GDB=∠FEC.”下列判断正确的是( )
A、 B、 C、 D、8. 小明和小亮一起研究一道数学题,如图,BD⊥AC于点D,E是边BC 上的一点,过点 E作 EF⊥AC于点F,点G在AB上,连结DG,GE.小明说:“如果还知道∠GDB=∠FEC,则能得到∠AGD=∠ABC.”小亮说:“如果∠AGD=∠ABC,可得到∠GDB=∠FEC.”下列判断正确的是( ) A、小明的说法正确,小亮的说法错误 B、小明的说法正确,小亮的说法正确 C、小明的说法错误,小亮的说法正确 D、小明的说法错误,小亮的说法错误9. 一个古称在称物时的状态如图所示,已知∠1=80°,则∠2 的度数为( )
A、小明的说法正确,小亮的说法错误 B、小明的说法正确,小亮的说法正确 C、小明的说法错误,小亮的说法正确 D、小明的说法错误,小亮的说法错误9. 一个古称在称物时的状态如图所示,已知∠1=80°,则∠2 的度数为( ) A、20° B、80° C、100° D、12010. 一副直角三角尺叠放如图1所示,现将含 角的三角尺ADE固定不动,将含 角的三角尺ABC绕顶点 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 )其他所有可能符合条件的度数为( )
A、20° B、80° C、100° D、12010. 一副直角三角尺叠放如图1所示,现将含 角的三角尺ADE固定不动,将含 角的三角尺ABC绕顶点 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 )其他所有可能符合条件的度数为( )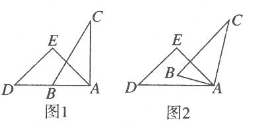 A、 和 B、 和 C、 和 D、以上都有可能
A、 和 B、 和 C、 和 D、以上都有可能二、填空题(共6小题,每小题3分,共18分)
-
11. ﹣125的立方根是 .
12. 如图,线段AB两端点的坐标分别为A(-1,0),B(1,1),把线段AB平移到CD位置,若线段CD两端点的坐标分别为C(1,a),D(b,4),则a+b的值为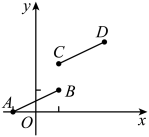 13. 如图,的边长为将向上平移个单位长度得到 , 且 , 则阴影部分的面积为 .
13. 如图,的边长为将向上平移个单位长度得到 , 且 , 则阴影部分的面积为 . 14. 如图,数轴上 , 两点表示的数分别为和4.1,则 , 两点之间表示整数的点共有个.
14. 如图,数轴上 , 两点表示的数分别为和4.1,则 , 两点之间表示整数的点共有个. 15. 一个小伙伴拿着如图的密码表玩听声音猜单词的游戏,若听到“咚咚一咚咚,咚一咚,咚咚咚一咚”表示的是“”,则听到“咚咚一咚,咚咚咚一咚咚,咚一咚咚咚”时,表示的是 .
15. 一个小伙伴拿着如图的密码表玩听声音猜单词的游戏,若听到“咚咚一咚咚,咚一咚,咚咚咚一咚”表示的是“”,则听到“咚咚一咚,咚咚咚一咚咚,咚一咚咚咚”时,表示的是 .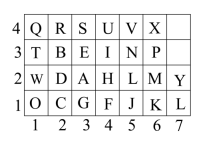 16. 如图,已知AB∥CD,E、F、H分别为AB、CD、AC上一点(∠DFK<∠BEK),KG平分∠EKF,∠AEK+∠HKE=180°.则下列结论:①CD∥KH;②∠BEK+∠DFK=2∠EKG;③∠BEK-∠DFK=∠GKH;④∠BAC+∠AGK-∠GKF+∠DFK=180°.其中正确的是 . (填序号)
16. 如图,已知AB∥CD,E、F、H分别为AB、CD、AC上一点(∠DFK<∠BEK),KG平分∠EKF,∠AEK+∠HKE=180°.则下列结论:①CD∥KH;②∠BEK+∠DFK=2∠EKG;③∠BEK-∠DFK=∠GKH;④∠BAC+∠AGK-∠GKF+∠DFK=180°.其中正确的是 . (填序号)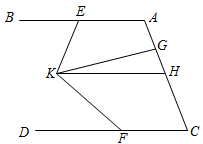
三、解答题(共8小题,共72分)
-
17.(1)、计算:;(2)、解方程:.18. 已知:如图, , , , , 求证: .
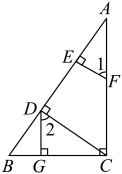
证明:∵ , (已知)
∴ , (垂直定义)
∴
∴( )
∴ ▲ ( )
∵(已知)
∴ ▲ (等量代换)
∴( )
∴ ▲ ( )
∵(已知)
∴(垂直定义)
∴ ▲ (等量代换)
∴(垂直定义)
19. 阅读材料,完成下列任务:因为无理数是无限不循环小数,因此无理数的小数部分我们不可能全部地写出来比如:、等,而常用的“…”或者“≈”的表示方法都不够百分百准确.
材料一:∵ , 即 ,
∴ .
∴的整数部分为1.
∴的小数部分为 .
材料二:我们还可以用以下方法求一个无理数的近似值.
我们知道面积是2的正方形的边长是 , 易知 , 因此可设 , 可画出如图示意图.由图中面积计算, , 另一方面由题意知 , 所以 .
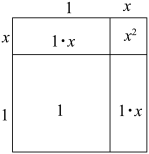
略去 , 得方程 , 解得 , 即 .
解决问题:
(1)、利用材料一中的方法,求的小数部分;(2)、利用材料二中的方法,探究的近似值.(画出示意图,标明数据,并写出求解过程)20.
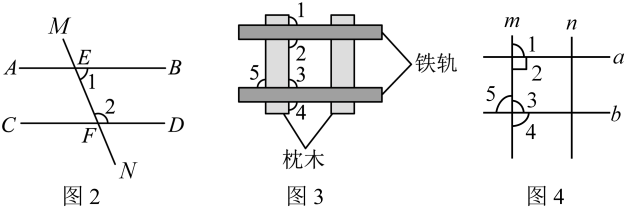 (1)、我们曾用移动三角尺的方法画出了两条平行线(如图1),请说明依据的基本事实为:;(2)、基本事实可作为依据,用来证明新的结论.请根据以上基本事实证明平行线的判定方法:“同旁内角互补,两直线平行”
(1)、我们曾用移动三角尺的方法画出了两条平行线(如图1),请说明依据的基本事实为:;(2)、基本事实可作为依据,用来证明新的结论.请根据以上基本事实证明平行线的判定方法:“同旁内角互补,两直线平行”已知:如图2,∠1和∠2是直线被直线截出的同旁内角,且与互补,求证: . (推理过程请注明理由)
(3)、平行线的判定在实际生活中有许多应用:如图3,在铺设铁轨时,两条铁轨必须是互相平行的.将铁轨和枕木看成直线(如图4 所示,直线a、b为直轨,m、n为枕木),是直角,可以通过度量图中已标出的哪个角的度数,来判断两条铁轨是否平行?为什么?21. 在如图所示的直角坐标系中,解答下列问题: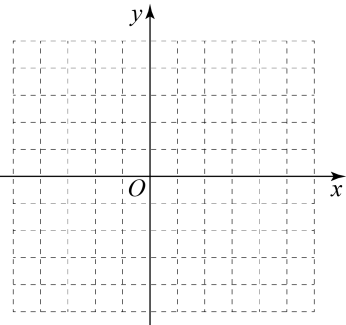 (1)、已知A(2,0),B(-1,-4),C(3,-3)三点,分别在坐标系中找出它们,并连接得到△ABC;(2)、将△ABC向上平移4个单位,得到△;(3)、求四边形的面积.22. 已知直线 , 点为直线 , 所确定的平面内的一点,
(1)、已知A(2,0),B(-1,-4),C(3,-3)三点,分别在坐标系中找出它们,并连接得到△ABC;(2)、将△ABC向上平移4个单位,得到△;(3)、求四边形的面积.22. 已知直线 , 点为直线 , 所确定的平面内的一点, (1)、问题提出:如图 , , 求的度数;(2)、问题迁移:如图 , 写出 , , 之间的数量关系,并说明理由;(3)、问题应用:如图 , :: , , , 求的值.23. 阅读下列材料,完成相应任务.
(1)、问题提出:如图 , , 求的度数;(2)、问题迁移:如图 , 写出 , , 之间的数量关系,并说明理由;(3)、问题应用:如图 , :: , , , 求的值.23. 阅读下列材料,完成相应任务.台球中的数学
如图1是台球桌面实物图,图2是抽象出的数学图形,已知长方形桌面中, , 一个球在桌面上的点处滚向桌边 , 碰到上的点后反弹,再碰到边上的点后,再次反弹进入底袋点 . 在球碰到桌边反弹的过程中,击出线与桌边的夹角等于反弹线与桌边的夹角 , 同理 .
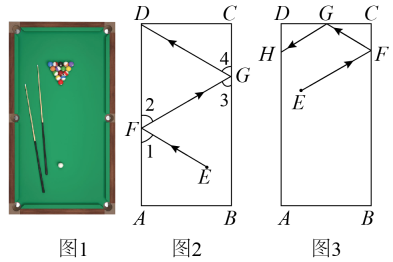 (1)、任务一:如图2,求证:;(2)、任务二:如图3,若球在桌面的点处,经过两次反弹后碰到边上的点处,若 , 请你判断与的位置关系,并说明理由.24. 综合与实践
(1)、任务一:如图2,求证:;(2)、任务二:如图3,若球在桌面的点处,经过两次反弹后碰到边上的点处,若 , 请你判断与的位置关系,并说明理由.24. 综合与实践如图. , , E,F是射线BC上的动点,且满足∠CAF=∠DAC,AE平分∠BAF.
 (1)、直线AD与BC有何位置关系?请说明理由.(2)、求∠CAE的度数.(3)、如图,将CD向右平移至处,并始终满足 , 是否存在某种情况,使 . 若存在,求出此时的度数;若不存在,请说明理由.
(1)、直线AD与BC有何位置关系?请说明理由.(2)、求∠CAE的度数.(3)、如图,将CD向右平移至处,并始终满足 , 是否存在某种情况,使 . 若存在,求出此时的度数;若不存在,请说明理由.