2023-2024学年湖北省八年级下学期数学期中仿真模拟卷三
试卷更新日期:2024-04-14 类型:期中考试
一、选择题(本大题共10小题,每小题3分,共计30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
-
1. 若有意义,则实数的取值范围为( )A、 B、 C、且 D、且2. 已知 , 且 , 化简二次根式的结果是( )A、 B、 C、 D、3. 下列各组数中,属于勾股数的是( )A、 , , B、 , , C、 , , D、 , ,4. 下列计算正确的是( )A、 B、 C、 D、5. 下列各式中,属于最简二次根式的是( )A、 B、 C、 D、6. 如图,在△ABC中,D,E分别是边 AB,BC的中点,点F 在射线DE 上.添加一个条件,使得四边形ADFC为平行四边形,则这个条件可以是( )
 A、∠B=∠F B、DE=EF C、AC=CF D、AD=CF7. 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )
A、∠B=∠F B、DE=EF C、AC=CF D、AD=CF7. 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )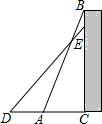 A、0.4 B、0.6 C、0.7 D、0.88. 如图,在中, , 于D, , E是斜边的中点,则的度数为( )
A、0.4 B、0.6 C、0.7 D、0.88. 如图,在中, , 于D, , E是斜边的中点,则的度数为( )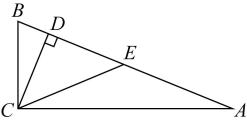 A、 B、 C、 D、9. 如图,直线AB∥CD,P是AB上的动点,当点P的位置变化时,三角形PCD的面积将( )
A、 B、 C、 D、9. 如图,直线AB∥CD,P是AB上的动点,当点P的位置变化时,三角形PCD的面积将( )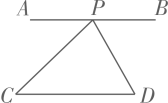 A、变大 B、变小 C、不变 D、无法确定10. 如图,四边形是菱形, 点M,N是对角线上的三等分点,点P是菱形边上的动点,则满足的点P的个数有( )
A、变大 B、变小 C、不变 D、无法确定10. 如图,四边形是菱形, 点M,N是对角线上的三等分点,点P是菱形边上的动点,则满足的点P的个数有( ) A、2个 B、4个 C、8个 D、12个
A、2个 B、4个 C、8个 D、12个二、填空题(本题共8小题,第11-14小题每题3分,第15-18小题每题4分,共28分)
-
11. 计算: .12. 把一个边长为1的正方形如图所示放在数轴上,以正方形的对角线为半径画弧交数轴于点 , 则点对应的实数是.
 13. 如图,圆柱的高为6cm,底面周长为16cm,蚂蚁在圆柱侧面爬行,从点A爬到点B的最短路程是cm.
13. 如图,圆柱的高为6cm,底面周长为16cm,蚂蚁在圆柱侧面爬行,从点A爬到点B的最短路程是cm. 14. 已知 , 则的值为 .15. 如图,点是的角平分线上的一点,过点作交于点C, , 若 , , 则 .
14. 已知 , 则的值为 .15. 如图,点是的角平分线上的一点,过点作交于点C, , 若 , , 则 .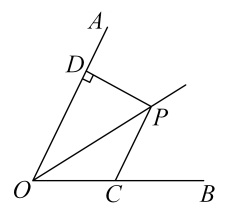 16. 实数 , 在数轴上的位置如图所示,则化简的结果是 .
16. 实数 , 在数轴上的位置如图所示,则化简的结果是 . 17. 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=4,则图中阴影部分的面积为
17. 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=4,则图中阴影部分的面积为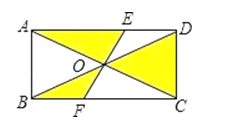 18. 正方形ABCD的边长为2,如图1,点E,F均在正方形内部,且BE=EF=FD,∠E=∠F=90°,则BE的长为;如图2,点G,H,I,J,K,L均在正方形内部,且BG=GH=HI=IJ=JK=KL=LD,∠G=∠H=∠I=∠J=∠K=∠L=90°,则BG的长为.
18. 正方形ABCD的边长为2,如图1,点E,F均在正方形内部,且BE=EF=FD,∠E=∠F=90°,则BE的长为;如图2,点G,H,I,J,K,L均在正方形内部,且BG=GH=HI=IJ=JK=KL=LD,∠G=∠H=∠I=∠J=∠K=∠L=90°,则BG的长为.
三、解答题(本题共7小题,共62分.解答应写出必要的文字说明、证明过程或演算步骤.)
-
19. 计算:(1)、(2)、(3)、20. 已知 , .(1)、试求的值;(2)、试求的值.21. 如图,已知点、为▱对角线上两点,且 , 连接 , 求证:
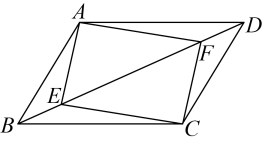 (1)、;(2)、四边形为平行四边形.22. 某校“综合与实践”小组开展了测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量,测量结果如下表(不完整).
(1)、;(2)、四边形为平行四边形.22. 某校“综合与实践”小组开展了测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量,测量结果如下表(不完整).课题
测量学校旗杆的高度
成员
组长: 组员: , ,
工具
皮尺等
测量示意图

说明:线段AB表示学校旗杆,垂直地面于点B,如图1,第一次将系在旗杆顶端的绳子垂直到地面,并多出了一段BC,用皮尺测出的长度;如图2,第二次将绳子拉直,绳子末端落在地面的点D处,用皮尺测出的距离.
测量数据
测量项目
数值
图1中的长度
1米
图2中的长度
米
…
…
(1)、根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆的高度.(2)、该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可).23. 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.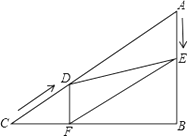 (1)、求证:AE=DF;(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)、当t为何值时,△DEF为直角三角形?请说明理由.24. 阅读材料:
(1)、求证:AE=DF;(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)、当t为何值时,△DEF为直角三角形?请说明理由.24. 阅读材料:基本不等式 ≤ (a>0,b>0),当且仅当a=b时等号成立,它是解决最值问题的有力工具.
例如:在x>0的条件下,当x为何值时,x+ 有最小值,最小值是多少?
解:∵x>0, >0∴ ≥ ,即 ≥2 ,∴ ≥2
当且仅当x= ,即x=1时,x+ 有最小值,最小值为2.
请根据阅读材料解答下列问题:
(1)、已知x>0,则当x为时,代数式3x+ 的最小值为;(2)、已知a>0,b>0,a2+b2=7,则ab的最大值为(3)、已知矩形面积为9,求矩形周长的最小值.25. 综合与实践实践操作:如图1,已知矩形纸片 .
第一步:如图2,将纸片沿折叠,使点B的对应点正好落在上,然后展平纸片,得到折痕;
第二步:如图3,在图2的基础上,沿折叠纸片,点C的对应点落在处,与交于点F.

问题解决:
(1)、如图2,判断四边形的形状,并证明;(2)、如图3,证明;(3)、若 , 则的周长为(直接写出答案即可).