2023-2024学年湖北省八年级下学期数学期中仿真模拟卷二
试卷更新日期:2024-04-14 类型:期中考试
一、精心选一选(本大题共8小题,每小题3分,满分24分.)
-
1. 下列各式中,属于二次根式的是( )A、 B、 C、 D、2. 由线段a,b,c组成的三角形是直角三角形的是( )A、a=2,b=3,c=4 B、 , , C、a=40,b=50,c=60 D、 , ,3. 如图,在平行四边形ABCD中,BC=10,AC=14,BD=8,则△BOC的周长是( )
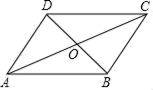 A、21 B、22 C、25 D、324. 下列计算正确的是( )A、 B、 C、 D、5. 如图,一棵大树在一次强台风中在距地面处折断,倒下后树顶端着地点距树底端的距离为 , 则这棵大树在折断前的高度为( )
A、21 B、22 C、25 D、324. 下列计算正确的是( )A、 B、 C、 D、5. 如图,一棵大树在一次强台风中在距地面处折断,倒下后树顶端着地点距树底端的距离为 , 则这棵大树在折断前的高度为( )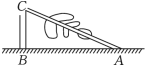 A、 B、 C、 D、6. 若二次根式,的值是整数,则下列n的取值符合条件的是( )A、 B、 C、 D、7. 如图,数轴上点A表示的数是0,点B表示的数是1, , 垂足为B,且 , 以A为圆心,长为半径画弧,与数轴交于点D,则点D表示的数为( )
A、 B、 C、 D、6. 若二次根式,的值是整数,则下列n的取值符合条件的是( )A、 B、 C、 D、7. 如图,数轴上点A表示的数是0,点B表示的数是1, , 垂足为B,且 , 以A为圆心,长为半径画弧,与数轴交于点D,则点D表示的数为( )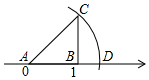 A、1.4 B、 C、 D、28. 如图,菱形中, , 与交于点 , 为延长线上的一点,且 , 连接分别交 , 于点、 , 连接 , 则下列结论:( )
A、1.4 B、 C、 D、28. 如图,菱形中, , 与交于点 , 为延长线上的一点,且 , 连接分别交 , 于点、 , 连接 , 则下列结论:( )
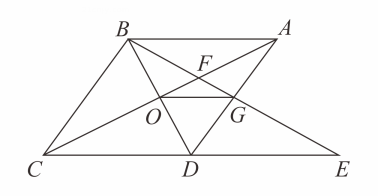
;与全等的三角形共有个;
;由点、、、构成的四边形是菱形.
A、 B、 C、 D、二、细心填一填(本大题共8小题,每小题3分,满分24分.)
-
9. 已知 则 的值是10. 观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:11. 已知 , 则的算术平方根是 .12. 在四边形ABCD中,AD∥BC,∠D=90°,要使它变成矩形,需要添加的一个条件是(写出一种情况即可).13. 若最简二次根式和能合并,则a的值为.14. 如图,在Rt△ABC中,∠B=90°,BC=4,AC=5,点D在边BC上.若以AD,CD为边,AC为对角线,作▱ADCE,则对角线DE的长的最小值为.
 15. 观察下列等式:
15. 观察下列等式:第1个等式:= ,
第个等式:= ,
第个等式: ,
第个等式:= ,
…
按上述规律,计算 .
16. 年国际数学家大会在北京召开,大会的会标是由我国古代数学家赵爽的“弦图”演变而来,体现了数学研究中的继承和发展如图是用八个全等的直角三角形拼接而成的“弦图”记图中正方形、正方形、正方形的面积分别为、、若正方形的边长为 , 则 .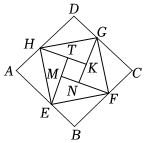
三、专心解一解(本大题共8小题,满分72分.)
-
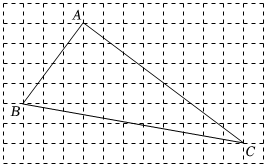
17. 计算:(1)、(2)、18. 如图,正方形网格中的每个小正方形的边长都是 , 点、、均在格点上.
 (1)、图中线段 , , ;(2)、求证:是直角三角形.19. 《西江月》中描述:平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…;翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺(尺)将它往前推进两步(尺),此时踏板升高离地五尺(尺),求秋千绳索的长度.
(1)、图中线段 , , ;(2)、求证:是直角三角形.19. 《西江月》中描述:平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…;翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺(尺)将它往前推进两步(尺),此时踏板升高离地五尺(尺),求秋千绳索的长度.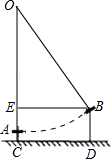 20. 请阅读下列材料:
20. 请阅读下列材料:问题:已知 , 求代数式的值.小敏的做法是:根据得 , , 得:.把作为整体代入:得.即:把已知条件适当变形,再整体代入解决问题.请你用上述方法解决下面问题:
(1)、已知 , 求代数式的值;(2)、已知 , 求代数式的值.21. 如图,在▱中,点、分别在、上,与相交于点 , 且.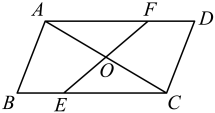 (1)、求证:≌;(2)、连接 , , 求证:四边形是平行四边形.22. 如图1,在中, , 于点C,点E是的中点,连接并延长,使 , 连接.
(1)、求证:≌;(2)、连接 , , 求证:四边形是平行四边形.22. 如图1,在中, , 于点C,点E是的中点,连接并延长,使 , 连接.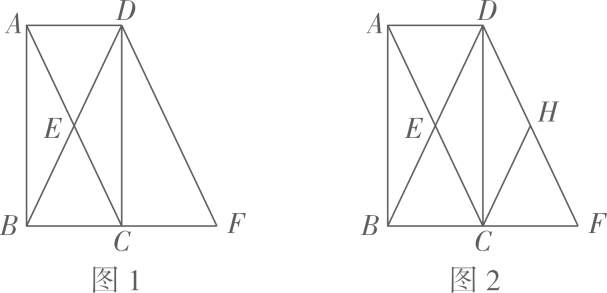 (1)、求证:四边形是矩形.(2)、如图2,点H为的中点,连结 , 若 , , 求四边形的面积.23. 中,D、E分别是 , 的中点,O是内任意一点,连接、 .
(1)、求证:四边形是矩形.(2)、如图2,点H为的中点,连结 , 若 , , 求四边形的面积.23. 中,D、E分别是 , 的中点,O是内任意一点,连接、 .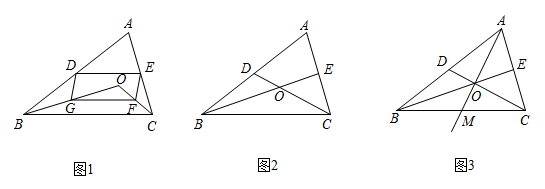 (1)、如图1,点G、F分别是、的中点,连接 , , , , 求证:四边形是平行四边形;(2)、如图2,若点O恰为和交点,求证: , ;(3)、如图3,若点O恰为和交点,射线与交于点M , 求证: .24. 如图,在中, , , . 点P从点B出发沿方向以每秒2个单位长度的速度向点C匀速运动,同时点Q从点A出发沿方向以每秒1个单位长度的速度向点C匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点P、Q运动的时间是t秒.过点P作于点M,连接、 .
(1)、如图1,点G、F分别是、的中点,连接 , , , , 求证:四边形是平行四边形;(2)、如图2,若点O恰为和交点,求证: , ;(3)、如图3,若点O恰为和交点,射线与交于点M , 求证: .24. 如图,在中, , , . 点P从点B出发沿方向以每秒2个单位长度的速度向点C匀速运动,同时点Q从点A出发沿方向以每秒1个单位长度的速度向点C匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点P、Q运动的时间是t秒.过点P作于点M,连接、 .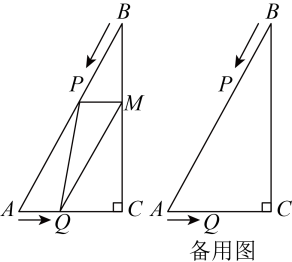 (1)、请用含有t的式子填空:
(1)、请用含有t的式子填空:, , ;
(2)、是否存在某一时刻使四边形为菱形?如果存在,求出相应的t值;如果不存在,说明理由.(3)、当t为何值时,为直角三角形?请说明理由.