2023-2024学年湖北省八年级下学期数学期中仿真模拟卷一

试卷更新日期：2024-04-14 类型：期中考试

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）下列各题中有且仅有一个正确答案，请在答题卡上将正确答案的标号涂黑

1. 若 $\frac{\sqrt{3 x - 6}}{x - 3}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥ $-$ 2且x≠3 B、x≠ $-$ 2 C、x≥2且x≠3 D、x≠2

查看试题解析
2. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{7}$ C、 $\sqrt{8}$ D、 $\sqrt{0.3}$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $2 \sqrt{2} - \sqrt{2} = 2$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{12} \div 3 = 2$

查看试题解析
4. 下列长度的三条线段能组成直角三角形的是（）

A、4，5，6 B、5，7，9 C、6，8，10 D、7，8，9

查看试题解析
5. 下列四组条件中，不能判定四边形ABCD为平行四边形的是（）

A、AB=CD，AD=BC B、AB∥CD，AB=CD C、AB=CD，AD∥BC D、AB∥CD，AD∥BC

查看试题解析
6. 如图，原来从 $A$ 村到 $B$ 村，需要沿路 $A \to C \to B (∠ C = 90 °)$ 绕过两地间的一片湖，在 $A$ ， $B$ 间建好桥后，就可直接从 $A$ 村到 $B$ 村 $.$ 若 $A C = 5 k m$ ， $B C = 12 k m$ ，那么，建好桥后从 $A$ 村到 $B$ 村比原来减少的路程为（）

A、 $2 k m$ B、 $4 k m$ C、 $10 k m$ D、 $14 k m$

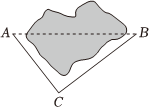查看试题解析
7. 在平行四边形ABCD中，∠A：∠B：∠C=2：3：2，则∠D=（　　）

A、36° B、108° C、72° D、60°

查看试题解析
8. 如图，在 $△ A B C$ 中， $A B = 5$ ， $A C = 11$ ，点 $D$ 在 $A C$ 上，若 $B D = C D = 6$ ， $A E$ 平分 $∠ B A C$ ，则 $A E$ 的长为（）

A、 $3$ B、 $4$ C、 $5$ D、 $6$

查看试题解析
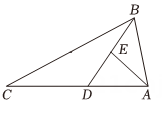9. 如图，数学实践活动课上小明用两根木条钉成一个角形框架 $∠ A O B$ ，且 $∠ A O B = 12 0^{°}$ ， $A O = B O = 4 c m$ ，将一根橡皮筋两端固定在点A，B处，拉展成线段AB，在平面内，拉动橡皮筋上的一点 $C$ ，当四边形OACB是菱形时，橡皮筋再次被拉长了（）

A、 $4 c m$ B、 $8 c m$ C、 $(8 - 4 \sqrt{3}) c m$ D、 $(4 - 2 \sqrt{3}) c m$

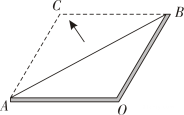查看试题解析
10. 如图，在Rt△ABC中，∠BAC=90°，AB=3，AC=4，分别以AB，AC，BC为边向△ABC外作正方形ABED，正方形ACHI，正方形BCGF．直线ED，HI交于点J，过点F作KF // HI，交DE于点K，过点G作GM // DE，与HI，KF分别交于点M，L. 则四边形KLMJ的面积为（）

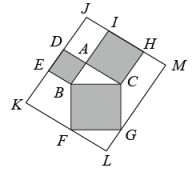A、90 B、100 C、110 D、120

查看试题解析

二、填空题（共6小题，每小题3分，共18分）

11. 化简： $\sqrt{2 \frac{2}{9}} =$ ．

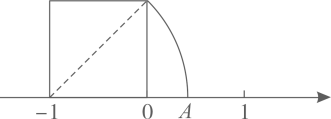
查看试题解析
12. 把一个边长为1的正方形如图所示放在数轴上，以正方形的对角线为半径画弧交数轴于点A，则点A对应的实数是．

查看试题解析
13. 如图， $D$ 、 $E$ 、 $F$ 、 $G$ 分别为 $A C$ 、 $A B$ 、 $B O$ 、 $C O$ 的中点， $∠ B O C = 90 °$ ，若 $A O = 3 ， B O = 4 ， C O = 3$ ，则四边形 $D E F G$ 的周长.

查看试题解析
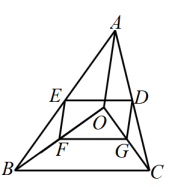14. 如图，菱形 $A B C D$ 的边长为2， $∠ A B C = 60 °$ ，对角线AC与BD交于点O，E为OB中点，F为AD中点，连接EF，则EF的长为．

查看试题解析
15. 如图，在Rt $△ A B C$ 中， $∠ B A C = 9 0^{°} ， A B = 6 ， A C = 8 ， P$ 为边BC上一个动点 $(P$ 不与B、C重合），PE⊥AB于 $E ， P F ⊥ A C$ 于F，M为EF中点，则AM的最小值是.

查看试题解析
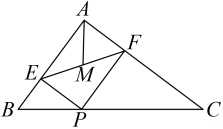16. 如图1所示，一个三角形纸片 $A B C$ 的尺寸为： $A B = 6 c m ， B C ＝ 4 c m ， A C ＝ 5 c m$ ，将其放置于图2所示的矩形纸板 $M N P Q$ 上，首先移动到 $△ A_{1} B C_{1}$ 的位置，接着又移动到 $△ A_{2} B_{1} C_{1}$ 的位置，其中点A，B， $C_{1}$ ， $A_{2}$ 均位于矩形纸板的边上.若在两次移动过程中，恰有 $∠ M A B = ∠ C_{1} A_{2} N = 30 °$ ，则线段 $A A_{2}$ 的长度等于.

查看试题解析

三、解答题（共8小题，共72分）

17. 计算下列各题

(1)、 $\sqrt{12} - \sqrt{3} (1 - \sqrt{6}) + 2 \sqrt{\frac{1}{2}}$ ；

(2)、 $(\sqrt{2} - \sqrt{3})^{2} - (2 + \sqrt{3}) (2 - \sqrt{3}) .$

查看试题解析
18. 如图，在△ABC中，D是BC中点，E是AD，BF的中点，AB＝AC.求证：四边形ADCF是矩形.

查看试题解析
19. 如图，某电信公司计划在A，B两乡镇间的E处修建一座5G信号塔，且使C，D两个村庄到E的距离相等.已知AD⊥AB于点A，BC⊥AB于点B，AB=80km，AD=50km，BC=30km，求5G信号塔E应该建在离A乡镇多少千米的地方？

查看试题解析
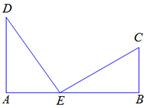20. 如图，矩形 $A B C D$ 内三个相邻的正方形的边长分别为m、n和1.

(1)、求图中阴影部分的面积（用含m和n的式子表示）；

(2)、若 $m = {(a + \frac{1}{a})}^{2} + 2 \sqrt{5}$ ， $n = a - \frac{1}{a} = \sqrt{5} - 1$ ，求阴影部分的面积.

查看试题解析
21. 如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点.

(1)、在图①中，以格点为端点，画线段MN＝ $\sqrt{13}$ ；

(2)、在图②中，以格点为顶点，画平行四边形ABCD，使它有一个锐角等于45°，且面积为6

查看试题解析
22. 如图，菱形ABCD的对角线AC、BD交于点O，过点B作BE∥AC，且 $B E = \frac{1}{2} A C$ ，连接EC、ED．

(1)、求证：四边形BECO是矩形；

(2)、若AC＝2，∠ABC＝60°，求DE的长．

查看试题解析
23. 如图，在一条绷紧的绳索一端系着一艘小船．河岸上一男孩拽着绳子另一端向右走，绳端从C移动到E，同时小船从A移动到B，且绳长始终保持不变．回答下列问题：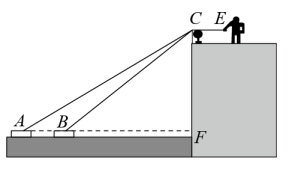

(1)、根据题意可知：ACBC＋CE（填“>”、“<”、“＝”）．

(2)、若CF＝5米，AF＝12米，AB＝9米，求小男孩需向右移动的距离．（结果保留根号）

查看试题解析
24. 如图

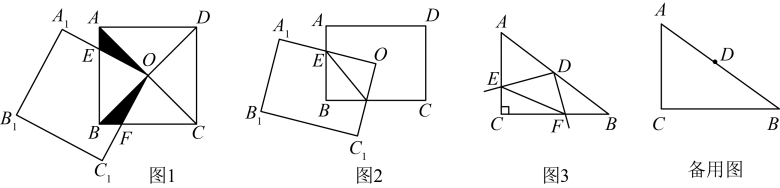(1)、【探索发现】如图1，正方形 $A B C D$ 的对角线相交于点O，点O又是正方形 $A_{1} B_{1} C_{1} O$ 的一个顶点，而且这两个正方形的边长相等，我们知道，无论正方形 $A_{1} B_{1} C_{1} O$ 绕点O怎么转动，总有 $Δ A E O ≅ Δ B F O$ ，连接 $E F$ ，求证： $A E^{2} + C F^{2} = E F^{2}$ ．

(2)、【类比迁移】如图2，矩形 $A B C D$ 的中心O是矩形 $A_{1} B_{1} C_{1} O$ 的一个顶点， $A_{1} O$ 与边 $A B$ 相交于点E， $C_{1} O$ 与边 $C B$ 相交于点F，连接 $E F$ ，矩形 $A_{1} B_{1} C_{1} O$ 可绕着点O旋转，判断（1）中的结论是否成立，若成立，请证明，若不成立，请说明理由；

(3)、【迁移拓展】如图3，在 $R t △ A C B$ 中， $∠ C = 90 °$ ， $A C = 3 c m$ ， $B C = 4 c m$ ，直角 $∠ E D F$ 的顶点D在边 $A B$ 的中点处，它的两条边 $D E$ 和 $D F$ 分别与直线 $A C ， B C$ 相交于点E，F， $∠ E D F$ 可绕着点D旋转，当 $B F = 1 c m$ 时，直接写出线段 $E F$ 的长度．

查看试题解析

2023-2024学年湖北省八年级下学期数学期中仿真模拟卷一

一、选择题（共10小题，每小题3分，共30分） 下列各题中有且仅有一个正确答案，请在答题卡上将正确答案的标号涂黑

二、填空题（共6小题，每小题3分，共18分）

三、解答题（共8小题，共72分）

一、选择题（共10小题，每小题3分，共30分）下列各题中有且仅有一个正确答案，请在答题卡上将正确答案的标号涂黑