2023-2024学年广西八年级下学期数学期中仿真模拟卷三

试卷更新日期：2024-04-14 类型：期中考试

进入出卷网下载

一、单项选择题（本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中只有一项是符合要求的)

1. 下列由线段a，b，c组成的三角形是直角三角形的为（　　）

A、 $a = 7 ， b = 24 ， c = 25$ B、 $a = 13 ， b = 14 ， c = 15$ C、 $a = \sqrt{3}$ ， $b = \sqrt{4}$ ， $c = \sqrt{5}$ D、 $a = 40 ， b = 50 ， c = 60$

查看试题解析
2. 若 $y = \sqrt{x - 2} + \sqrt{4 - 2 x} - 3$ ，则 $(x + y)^{2022}$ 等于（）

A、 $1$ B、 $5$ C、 $- 5$ D、 $- 1$

查看试题解析
3. 下列二次根式中，能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{4}$ C、 $\sqrt{12}$ D、 $\sqrt{24}$

查看试题解析
4. 下列运算正确的是（）

A、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ B、 $(2 \sqrt{3})^{2} = 6$ C、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ D、 $\sqrt{(- 2)^{2}} = - 2$

查看试题解析
5. 如图，在四边形 ABCD中，对角线 AC 和 BD 相交于点O.下列条件中，不能判定四边形ABCD为平行四边形的是（）

A、AB∥DC，AD∥BC B、AB=DC，AD=BC C、AB∥DC，AD=BC D、OA=OC，OB=O

查看试题解析
6. 若直角三角形一条直角边长为6，斜边长为10，则斜边上的高是（　　）

A、 $\frac{12}{5}$ B、 $\frac{24}{5}$ C、5 D、10

查看试题解析
7. 如图所示的是由一个直角三角形和三个正方形组成的图形，若其中 $S_{正方形 A B E D} = 16 c m^{2}$ ， $S_{正方形 A H I C} = 25 c m^{2}$ ，则正方形 $B C F G$ 的面积是（）

A、 $3 c m^{2}$ B、 $9 c m^{2}$ C、 $16 c m^{2}$ D、 $41 c m^{2}$

查看试题解析
8. 如图，点A在平行四边形的对角线上，则图中两个阴影三角形的面积S₁，S₂的大小关系是（）

A、 $S_{1} = S_{2}$ B、 $S_{1} > S_{2}$ C、 $S_{1} < S_{2}$ D、无法确定

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = 12$ ， $A C = 9$ ， $B C = 15$ ， P为 $B C$ 边上一动点， $P E ⊥ A B$ 于点E ， $P F ⊥ A C$ 于点F ，则 $E F$ 的最小值为（）

A、 $7.2$ B、 $7.5$ C、 $6.5$ D、6

查看试题解析
10. 已知n是正整数， $\sqrt{3 n}$ 是整数，则n的最小值是（）

A、0 B、1 C、3 D、－3

查看试题解析
11. 现有一个圆柱体水晶杯（容器厚度忽略不计），其底面圆的周长为 $16 c m$ ，高为 $15 c m$ ，在杯子内壁离容器底部 $4.5 c m$ 的点B处有一滴蜂蜜，与蜂蜜相对，此时一只蚂蚁正好在杯子外壁，离容器上沿 $4.5 c m$ 的点A处，则蚂蚁吃到蜂蜜需爬行的最短路径为（）

A、 $17 c m$ B、 $10 c m$ C、 $2 \sqrt{73} c m$ D、 $16 c m$

查看试题解析
12. 如图，在矩形ABCD中，O为AC的中点，过点O作AC的垂线，分别交DC于点F，交AB于点E，G是AE的中点，且∠AOG=30°，有下列结论：①DC=3OG；②OG= $\frac{1}{2}$ BC；③连结AF，CE，四边形AECF为菱形；④ $S_{△ A O E} = \frac{1}{6} S_{矩形 A B C D}$ 其中正确的是（）

A、②③ B、③④ C、①②④ D、①③④

查看试题解析

二、填空题（本大题共6小题，每小题2分，共12分。）

13. 若6，11，m为三角形的三边长，则化简 $\sqrt{{(5 - m)}^{2}} + m$ 的结果为．

查看试题解析
14. 如图，▱ $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ，若 $S_{△ A O B} = 2$ ，则▱ $A B C D$ 的面积为．

查看试题解析
15. 如图，九洞天风景区内的路 $A C ， B C$ 互相垂直，路 $A B$ 的中点 $P$ 与点 $C$ 被经过景区的六冲河隔开．若测得路 $A B$ 的长为 $100 m$ ，则 $P$ 、 $C$ 两点间的距离．

查看试题解析
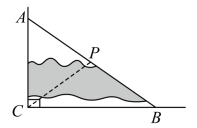16. 正方形 $A B C D$ 的边长为 $3$ ，点 $E ， F$ 分别是对角线上的两点，过点 $E ， F$ 分别作 $A D ， A B$ 的平行线，则图中阴影部分的面积等于．

查看试题解析
17. 已知实数 $a$ 在数轴上的位置如图所示，则化简 $\sqrt{{(a - 2)}^{2}} + a - 1$ $=$ ．

查看试题解析
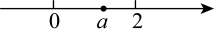18. 如图，在矩形ABCD中， $A B = 3$ ， $B C = 4$ ， $M$ 是 $C D$ 边上任意一点，过点A、C、D作射线 $B M$ 的垂线，垂足分别是E、F、G，若 $A E + C F + D G = m$ ，则m的最小值是．

查看试题解析

三、解答题（共8题，共72分）

19. 计算：

(1)、 $4 \sqrt{5} + \sqrt{45} - 4 \sqrt{2} \div \sqrt{8}$ ；

(2)、 ${(\sqrt{2} + 1)}^{2} - (\sqrt{3} + 1) (\sqrt{3} - 1)$ ．

查看试题解析
20. 已知 $a = \sqrt{3} - \sqrt{2}$ ， $b = \sqrt{3} + \sqrt{2}$ ，求 $a^{2} + 3 a b + b^{2} - a + b$ 的值．

查看试题解析
21. 如图，四边形ABCD是平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E.

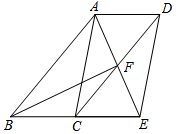(1)、求证：BE＝CD；

(2)、若BF恰好平分∠ABE，连接AC、DE，求证：四边形ACED是平行四边形.

查看试题解析
22. 一款名为超级玛丽的游戏中，玛丽到达一个高为10米的高台A后，利用旗杆顶部的绳索，划过90°到达与高台A水平距离为17米，高为3米的矮台B．

(1)、求旗杆的高度OM；

(2)、玛丽在荡绳索过程中离地面的最低点的高度MN．

查看试题解析
23. 如图，已知 $▱ A B C D$ 的对角线 $A C$ ， $B D$ 交于点O， $E F$ 过点O且与 $A B$ ， $C D$ 分别相交于点E、F．

(1)、求证： $O E = O F$ ；

(2)、若 $∠ F E B = 90 °$ ， $B E = 15$ ， $B D = 34$ ，求 $E F$ 的长．

查看试题解析
24. 如图，矩形ABCD中，BC=2AB，点E是边AD的中点，点F是线段AE上一点（点F不与点A，E重合），连接BF，过点F作直线BF的垂线，与线段CE交于点G，连接BG，点H是线段BG的中点．

(1)、若CE=2 $\sqrt{2}$ ，求矩形ABCD的面积；

(2)、求证：BF= $\sqrt{2}$ EH.

查看试题解析
25. 阅读下面的解题过程，体会如何发现隐含条件并回答下面的问题：
化简： $(\sqrt{1 - 3 x})^{2} - | 1 - x |$
解：隐含条件 $1 - 3 x \geq 0$ ，解得： $x \leq \frac{1}{3}$
∴ $1 - x > 0$
∴原式 $= (1 - 3 x) - (1 - x) = 1 - 3 x - 1 + x = - 2 x$

(1)、【启发应用】
按照上面的解法，试化简 $\sqrt{(3 - x)^{2}} - (\sqrt{2 - x})^{2}$ ；

(2)、【类比迁移】
实数a，b在数轴上的位置如图所示，化简： $\sqrt{a^{2}} + \sqrt{(a + b)^{2}} - | b - a |$ ；

(3)、已知a，b，c为 $△ A B C$ 的三边长．化简： $\sqrt{(a + b + c)^{2}} + \sqrt{(a - b - c)^{2}} + \sqrt{(b - a - c)^{2}} + \sqrt{(c - b - a)^{2}}$ ．

查看试题解析
26. 如图，在矩形 $A B C D$ 中， $A B = 8 c m$ ， $B C = 6 c m$ ．动点 $P$ 、 $Q$ 分别从点 $A$ 、 $C$ 以2cm/s的速度同时出发．动点 $P$ 沿 $A B$ 向终点 $B$ 运动，动点 $Q$ 沿 $C D$ 向终点 $D$ 运动，连结 $P Q$ 交对角线 $A C$ 于点 $O$ ．设点 $P$ 的运动时间为 $t (s)$ ．

(1)、当四边形 $A P Q D$ 是矩形时，求出 $t$ 的值．

(2)、当四边形 $A P C Q$ 是菱形时，求 $t$ 的值．

(3)、当 $△ A P O$ 是等腰三角形时，直接写出 $t$ 的值．

查看试题解析