2024年北师大版数学八年级下册周测卷(第六章第3-4节)培优卷
试卷更新日期:2024-04-14 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,平行四边形的对角线 , 交于点 , 已知 , , 的周长为15,则的长为( )
 A、5 B、6 C、7 D、82. 如图,在正方形中,点E , F分别是 , 的中点, , 相交于点M , G为上一点,N为的中点.若 , , 则线段的长度为( )
A、5 B、6 C、7 D、82. 如图,在正方形中,点E , F分别是 , 的中点, , 相交于点M , G为上一点,N为的中点.若 , , 则线段的长度为( )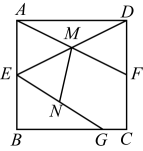 A、 B、 C、2 D、3. 如图,▱ABCD的对角线AC、BD交于点O,▱ABCD的周长为30,直线EF过点O,且与AD,BC分别交于点E.F,若OE=5,则四边形ABFE的周长是( )
A、 B、 C、2 D、3. 如图,▱ABCD的对角线AC、BD交于点O,▱ABCD的周长为30,直线EF过点O,且与AD,BC分别交于点E.F,若OE=5,则四边形ABFE的周长是( ) A、30 B、25 C、20 D、154. 如图,的对角线 , 相交于点 , 的平分线与边相交于点 , 是中点,若 , , 则的长为( )
A、30 B、25 C、20 D、154. 如图,的对角线 , 相交于点 , 的平分线与边相交于点 , 是中点,若 , , 则的长为( ) A、1 B、2 C、3 D、45. 如图,在 中,点D,E分别是 , 边的中点,点F在 的延长线上.添加一个条件,使得四边形 为平行四边形,则这个条件可以是( )
A、1 B、2 C、3 D、45. 如图,在 中,点D,E分别是 , 边的中点,点F在 的延长线上.添加一个条件,使得四边形 为平行四边形,则这个条件可以是( ) A、 B、 C、 D、6. 如图,在 中, , , ,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为( )
A、 B、 C、 D、6. 如图,在 中, , , ,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为( ) A、6 B、9 C、12 D、157. 下列多边形中,内角和等于的是( )A、
A、6 B、9 C、12 D、157. 下列多边形中,内角和等于的是( )A、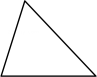 B、
B、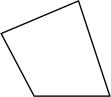 C、
C、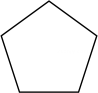 D、
D、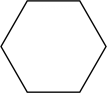 8. 如图,、、 , 是六边形的四个外角,延长交于点若 , 则的度数为( )
8. 如图,、、 , 是六边形的四个外角,延长交于点若 , 则的度数为( ) A、 B、 C、 D、9. 如图,将一副直角三角板按图中所示的位置摆放,两条斜边互相平行,则∠1=( )
A、 B、 C、 D、9. 如图,将一副直角三角板按图中所示的位置摆放,两条斜边互相平行,则∠1=( ) A、 B、 C、 D、10. 如图,将三角形纸片沿折叠,当点A落在四边形的外部时,测量得 , , 则为( )
A、 B、 C、 D、10. 如图,将三角形纸片沿折叠,当点A落在四边形的外部时,测量得 , , 则为( )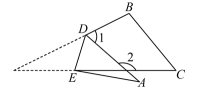 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 如图,是五边形的一个外角.若 , 则的度数为 .
 12. 在周长为800米的三角形地块中修建如图所示的三条水渠,则水渠总长为米.
12. 在周长为800米的三角形地块中修建如图所示的三条水渠,则水渠总长为米. 13. 如图,小华在一个不完整的正多边形图案中,量得一边与一条对角线的夹角∠ACB=15°,则这个正多边形的边数是.
13. 如图,小华在一个不完整的正多边形图案中,量得一边与一条对角线的夹角∠ACB=15°,则这个正多边形的边数是. 14. 如图,在四边形中, , , 分别是 , 的中点,已知 , , 则 .
14. 如图,在四边形中, , , 分别是 , 的中点,已知 , , 则 . 15. 如图,△ABC的周长为 28,点 D,E都在边BC 上,∠ABC 的平分线垂直于 AE,垂足为 Q,∠ACB的平分线垂直于 AD,垂足为 P,连结PQ.若 BC=10,则PQ的长是.
15. 如图,△ABC的周长为 28,点 D,E都在边BC 上,∠ABC 的平分线垂直于 AE,垂足为 Q,∠ACB的平分线垂直于 AD,垂足为 P,连结PQ.若 BC=10,则PQ的长是. 16. 如图,已知在△ABC 中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点 C 作CG⊥AD于点F,交 AB 于点 G,连结EF,则线段 EF 的长为.
16. 如图,已知在△ABC 中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点 C 作CG⊥AD于点F,交 AB 于点 G,连结EF,则线段 EF 的长为.
三、解答题(共8题,共72分)
-
17. 如图,在四边形ABCD中,∠D=90° ,E是BC边上一点,EF⊥AE,交CD于点F.
 (1)、若∠EAD= 60°,求∠DFE的度数;(2)、若CAEB=∠CEF,AE平分∠BAD,求证:∠B=∠C.18. 如图,在△ABC中,∠BAC=70°,∠ABC 和∠ACB的平分线相交于点 D,E,F,G,H 分别是线段 AB,AC,BD,CD的中点.
(1)、若∠EAD= 60°,求∠DFE的度数;(2)、若CAEB=∠CEF,AE平分∠BAD,求证:∠B=∠C.18. 如图,在△ABC中,∠BAC=70°,∠ABC 和∠ACB的平分线相交于点 D,E,F,G,H 分别是线段 AB,AC,BD,CD的中点.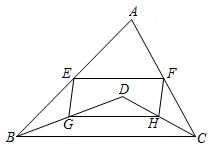 (1)、求∠BDC的度数.(2)、连结 EG,EF,HG,HF,求证:四边形EGHF 是平行四边形.19. 如图,DE是△ABC的中位线,延长DE至F , 使EF=DE , 连接BF .
(1)、求∠BDC的度数.(2)、连结 EG,EF,HG,HF,求证:四边形EGHF 是平行四边形.19. 如图,DE是△ABC的中位线,延长DE至F , 使EF=DE , 连接BF . (1)、求证:四边形ABFD是平行四边形;(2)、求证:BF=DC .20. 如图,的中线 , 相交于点G,点P,Q分别是 , 的中点.求证:
(1)、求证:四边形ABFD是平行四边形;(2)、求证:BF=DC .20. 如图,的中线 , 相交于点G,点P,Q分别是 , 的中点.求证: (1)、四边形是平行四边形;(2)、 .21. 阅读与思考
(1)、四边形是平行四边形;(2)、 .21. 阅读与思考请阅读下列材料,并完成相应的任务.
年月日星期一
今天,同学们学习了三角形中位线定理的相关内容,知道了“三角形的中位线平行于第三边,且等于第三边的一半”.课下,对三角形中位线定理的相关知识进行了复习,并对它相关的命题产生了兴趣.如图1,在中,分别是边上的点,同学们提出了以下三个命题:
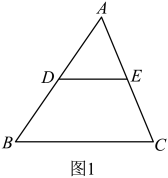
I.若是边的中点,且 , 则是边的中点.
II.若 , 且 , 则分别是边的中点.
III.若是边的中点,且 , 则是边的中点.
任务:
(1)、从所提出的三个命题中选择一个假命题,并在图2中画出反例.(要求:尺规作图,保留作图痕迹) (2)、从所提出的三个命题中选择一个真命题进行证明.22. 数学兴趣小组学习了三角形的外角性质1三角形的一个外角等于与它不相邻的两个内角和.提出问题:四边形的一个外角与它不相邻的内角之和具有怎样的数量关系?
(2)、从所提出的三个命题中选择一个真命题进行证明.22. 数学兴趣小组学习了三角形的外角性质1三角形的一个外角等于与它不相邻的两个内角和.提出问题:四边形的一个外角与它不相邻的内角之和具有怎样的数量关系?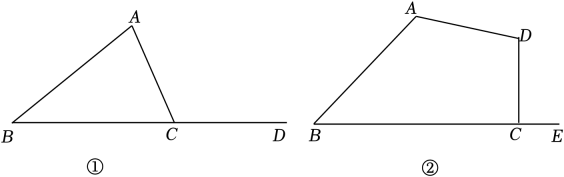 (1)、【回顾】如图①.请直接写出与、之间的数量关系: .(2)、【探究】如图②,已知是四边形的外角,求、、与的数量关系.请补全下面解答过程.
(1)、【回顾】如图①.请直接写出与、之间的数量关系: .(2)、【探究】如图②,已知是四边形的外角,求、、与的数量关系.请补全下面解答过程.解:∵是四边形的外角.
∴ ▲ .
∴ ▲ .
∵ ▲ .
∴ ▲ ▲ .
∴ ▲ .

