2023-2024学年广西八年级下学期数学期中仿真模拟卷一

试卷更新日期：2024-04-14 类型：期中考试

进入出卷网下载

一、单项选择题（本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中只有一项是符合要求的)

1. 式子 $\sqrt{n + 1}$ 在实数范围内有意义，则n的取值范围为（）

A、 $n \leq - 1$ B、 $n < 1$ C、 $n \geq - 1$ D、 $n > 1$

查看试题解析
2. 下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（）

A、 $\sqrt{3}$ 、 $\sqrt{4}$ 、 $\sqrt{5}$ B、2、3、4 C、6、7、8 D、9、12、15

查看试题解析
3. 下列各式中不是二次根式的是（）

A、 $\sqrt{x^{2} + 1}$ B、 $\sqrt{- 9}$ C、 $- \sqrt{5}$ D、 $\sqrt{{(m - n)}^{2}}$

查看试题解析
4. 已知最简二次根式 $\sqrt{2 a - 4}$ 与 $\sqrt{2}$ 是同类二次根式，则a的值是（　　）

A、2 B、3 C、4 D、5

查看试题解析
5. 下列计算错误的是（　　）

A、 $4 \sqrt{3} + 2 \sqrt{3} = 6 \sqrt{3}$ B、 $4 \sqrt{3} - 2 \sqrt{3} = 2 \sqrt{3}$ C、 $4 \sqrt{3} \div 2 \sqrt{3} = 2$ D、 $4 \sqrt{3} \times 2 \sqrt{3} = 8 \sqrt{3}$

查看试题解析
6. 如图，在 ▱ ABCD中，有下列条件：①AC=BD.②∠1+∠3=90°.③OB= $\frac{1}{2}$ AC.④∠1=∠2.其中能判定 ▱ ABCD是矩形的有（）

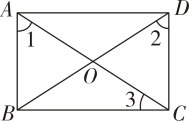A、① B、①②③ C、②③④ D、①②③④

查看试题解析
7. 已知实数 $a$ 在数轴上的对应点的位置如图所示，则 $\sqrt{(a - 3)^{2}} + \sqrt{(a - 10)^{2}}$ 化简后等于（）

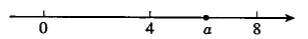A、7
B、-7
C、 $2 a - 13$ D、 $- 2 a + 13$

查看试题解析
8. 如图，在赵爽弦图中，已知直角三角形的短直角边长为 $a$ ，长直角边长为 $b$ ，大正方形的面积为20，小正方形的面积为4，则 $a b$ 的值是（）

A、10 B、9 C、8 D、7

查看试题解析
9. 如图，平行四边形 $A B C D$ 的对角线 $A C$ ， $B D$ 交于点 $O$ ，已知 $B D = 10$ ， $A C = 6$ ， $△ B O C$ 的周长为15，则 $A D$ 的长为（）

A、5 B、6 C、7 D、8

查看试题解析
10. 如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF＝3，则菱形ABCD的周长为（）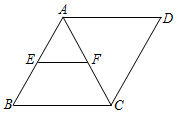

A、24 B、18 C、12 D、9

查看试题解析
11. 为了方便体温监测，某学校在大门入口的正上方 $A$ 处装有红外线激光测温仪（如图所示），测温仪离地面的距离 $A B = 2.2$ 米，当人体进入感应范围内时，测温仪就会自动测温并报告人体体温．当身高为1.7米的小明 $C D$ 正对门缓慢走到离门1.2米处时（即 $B C = 1.2$ 米），测温仪自动显示体温，此时小明头顶到测温仪的距离 $A D$ 等于（）

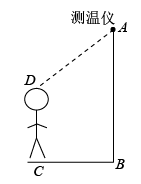A、0.5米 B、1.2米 C、1.3米 D、1.7米

查看试题解析
12. 宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ （约0.618）的矩形叫做黄金矩形，黄金矩形蕴藏着丰富的美学价值，我们可以折叠出一个黄金矩形．第一步，在一张矩形纸片的一端利用图1的方法折出一个正方形，然后把纸片展平；第二步，如图2，把这个正方形折成两个相等的矩形，再把纸片展平，折痕是 $A H$ ；第三步，折出内侧矩形的对角线 $A B$ ，并把 $A B$ 折到图3中所示的 $A D$ 处，折痕为 $A E$ ；第四步，如图4，展平纸片，按照所得的点 $D$ 折出 $D F$ ，使 $D F ⊥ M E$ ．则下列是黄金矩形的是（）

A、矩形 $M N A H$ B、矩形 $A C B H$ C、矩形 $B C D F$ D、矩形 $M N C B$

查看试题解析

二、填空题（本大题共6小题，每小题2分，共12分。）

13. 下列是最简二次根式的有．
① $\sqrt{12}$ ；② $\sqrt{15}$ ；③ $\sqrt{\frac{1}{5}}$ ；④ $\sqrt{a^{2} + b^{2}}$ ．

查看试题解析
14. 若y $= \sqrt{x - 2} + \sqrt{2 - x} + \sqrt{3}$ ，则xy＝．

查看试题解析
15. 在 $▱$ ABCD中，已知AB=15，AC=13，BC边上的高等于12，则 $▱$ ABCD的周长是 .

查看试题解析
16. 如图是一台多功能手机支架，图2是其侧面示意图， $D E$ 为地面，支架 $C D$ 垂直地面， $A B ， B C$ 可分别绕点B ， C转动，测量知 $A B = 30$ cm， $B C = 20$ cm， $C D = 15$ cm．当 $A B ， B C$ 转动到 $∠ B C D = 120 °$ ，且A ， C ， D三点共线时，则点A到地面的距离为cm．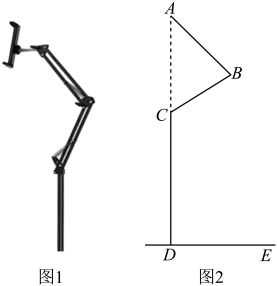

查看试题解析
17. 出人相补原理是我国古代数学的重要成就之一最早是由三国时期数学家刘徽创建．“将一个几何图形，任意切成多块小图形，几何图形的总面积保持不变，等于所分割成的小图形的面积之和”是该原理的重要内容之一，如图，在矩形ABCD中，AB=5，AD=12，对角线AC与BD交于点O，点E为BC边上的一个动点，EF⊥AC，EG⊥BD，垂足分别为F，G，则EF+EG= ．

查看试题解析
18. 如图，在一张长为7cm，宽为5cm的矩形纸片上，现要剪下一个腰长为4cm的等腰三角形，要求：等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上，则剪下的等腰三角形一腰上的高为.

查看试题解析

三、解答题（共8题，共72分）

19. 计算：

(1)、 $\sqrt{12} - \sqrt{18} \times \sqrt{\frac{3}{2}}$ ；

(2)、 $(4 \sqrt{2} - 3 \sqrt{6}) \div 2 \sqrt{2}$ ．

查看试题解析
20. 已知： $x = \sqrt{5}$ ， $y = \sqrt{5} - 2$ ，求代数式 $x^{2} - 3 x y + y^{2}$ 的值

查看试题解析
21. 如图，在▱ABCD中，AC，BD相交于点O，且AO=BO，∠ADB的平分线交AB于点E.

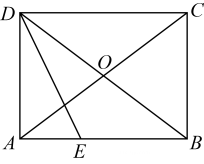(1)、求证：▱ABCD是矩形.

(2)、若AB=8，OC=5，求AE的长.

查看试题解析
22. 如图，在 $▱ A B C D$ 中，点 $E$ ， $F$ 分别在 $A D$ 、 $B C$ 上，且 $A E = C F$ ，连接 $E F$ ， $A C$ 交于点 $O$ ．求证： $O E = O F$ ．

查看试题解析
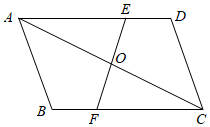23. 如图，在Rt△ABC中，∠B＝90°，AC＝60 cm，∠A＝60°，点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是t秒(0＜t≤15)．过点D作DF⊥BC于点F，连结DE，EF.

(1)、四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；

(2)、当t为何值时，△DEF为直角三角形？请说明理由．

查看试题解析
24. 如图，在一条东四走向河流的一侧有一村庄 $C$ ，河边原有两个取水点A、B，道路 $A C$ 因为施工需要封闭，该村为方便村民取水，决定在河边新建一个取水点H（A，H，B在同一条直线上），并新修一条道路 $C H$ ，已知 $C B = \sqrt{5}$ 千米， $C H = 2$ 千米， $H B = 1$ 千米．

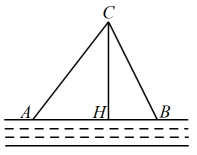(1)、 $C H$ 是否为村庄C到河边最近的道路，请通过计算加以说明；

(2)、已知新的取水点H与原取水点A相距 $1.5$ 千米，求新路 $C H$ 比原路 $C A$ 少多少千米．

查看试题解析
25. 【阅读材料】宾宾在学习二次根式时，发现一些含根号的式子可以化成另一个式子的平方，
如： $5 + 2 \sqrt{6} = (2 + 3) + 2 \sqrt{2 \times 3} = {(\sqrt{2})}^{2} + {(\sqrt{3})}^{2} + 2 \sqrt{2} \times \sqrt{3} = {(\sqrt{2} + \sqrt{3})}^{2}$ ；

$8 + 2 \sqrt{7} = (1 + 7) + 2 \sqrt{1 \times 7} = 1^{2} + {(\sqrt{7})}^{2} + 2 \times 1 \times \sqrt{7} = {(1 + \sqrt{7})}^{2}$ .

(1)、【类比归纳】
请你仿照宾宾的方法将 $7 + 2 \sqrt{10}$ 化成另一个式子的平方；

(2)、请运用宾宾的方法化简； $\sqrt{11 - 6 \sqrt{2}}$ .

(3)、【变式探究】
若 $a \pm 2 \sqrt{21} = {(\sqrt{m} + \sqrt{n})}^{2}$ ，且a，m，n均为正整数，则 $a =$ .

查看试题解析
26. 在几何探究问题中，经常需要通过作辅助线（如，连接两点，过某点作垂线，作延长线，作平行线等等）把分散的条件相对集中，以达到解决问题的目的.

(1)、（探究发现）如图1，点E，F分别在正方形ABCD的边BC，CD上， $∠ E A F = 45 °$ ，连接EF.通过探究，可发现BE，EF，DF之间的数量关系为（直接写出结果）.

(2)、（验证猜想）同学们讨论得出下列三种证明思路（如图1）：
思路一：过点A作 $A G ⊥ A E$ ，交CD的延长线于点G.

思路二：过点A作 $A G ⊥ A E$ ，并截取 $A G = A E$ ，连接DG.

思路三：延长CD至点G，使 $D G = B E$ ，连接AG.

请选择你喜欢的一种思路证明（探究发现）中的结论.

(3)、（迁移应用）如图2，点E，F分别在正方形ABCD的边BC，CD上，且 $B C = 3 B E$ ， $∠ E A F = 45 °$ ，设 $B E = a$ ，试用含 $a$ 的代数式表示DF的长.

查看试题解析