2023-2024学年广西七年级下学期数学期中仿真模拟卷三
试卷更新日期:2024-04-14 类型:期中考试
一、单项选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中只有一项是符合要求的)
-
1. 在﹣2, , ,3.14, , ,这6个数中,无理数共有( )
A、4个 B、3个 C、2个 D、1个2. 如图,直线与相交于点 , 平分 , 且 , 则为( )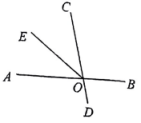 A、 B、 C、 D、3. 如图,点M , N处各安装一个路灯,点P处竖有一广告牌,测得 , 则点P到直线的距离可能为( )
A、 B、 C、 D、3. 如图,点M , N处各安装一个路灯,点P处竖有一广告牌,测得 , 则点P到直线的距离可能为( ) A、7m B、6m C、m D、4m4. 如图,下列条件中,能判定 AD∥BE 的是( )
A、7m B、6m C、m D、4m4. 如图,下列条件中,能判定 AD∥BE 的是( ) A、∠1=∠2 B、∠3=∠4 C、∠B+∠ADC=180° D、∠B=∠DCE5. 下列选项中的车标图案可以看着是由“基本图案”经过平移得到的是( )A、
A、∠1=∠2 B、∠3=∠4 C、∠B+∠ADC=180° D、∠B=∠DCE5. 下列选项中的车标图案可以看着是由“基本图案”经过平移得到的是( )A、 B、
B、 C、
C、 D、
D、 6. 16的算术平方根是( )A、16 B、4 C、﹣4 D、±47. 点P(m+3,m﹣2)在直角坐标系的x轴上,则点P的坐标为( )A、(0,5) B、(5,0) C、(﹣5,0) D、(0,﹣5)8. 如图,直线AB,AF被BC所截,与∠2是同位角的是( )
6. 16的算术平方根是( )A、16 B、4 C、﹣4 D、±47. 点P(m+3,m﹣2)在直角坐标系的x轴上,则点P的坐标为( )A、(0,5) B、(5,0) C、(﹣5,0) D、(0,﹣5)8. 如图,直线AB,AF被BC所截,与∠2是同位角的是( ) A、∠1 B、∠5 C、∠3 D、∠49. 下列说法中,正确的是( )A、两条不相交的直线叫做平行线 B、在同一平面内,一条直线的平行线有无数条 C、在同一平面内,两条直线一定相交 D、经过一点有且只有一条直线与已 知直线平行10. 如图,AB∥CD,直线 EF 分别交AB,CD于点E,F,EG 平分∠BEF,交 CD 于点 G.若∠FEG=58°,则∠EGD的度数为( )
A、∠1 B、∠5 C、∠3 D、∠49. 下列说法中,正确的是( )A、两条不相交的直线叫做平行线 B、在同一平面内,一条直线的平行线有无数条 C、在同一平面内,两条直线一定相交 D、经过一点有且只有一条直线与已 知直线平行10. 如图,AB∥CD,直线 EF 分别交AB,CD于点E,F,EG 平分∠BEF,交 CD 于点 G.若∠FEG=58°,则∠EGD的度数为( ) A、132° B、128° C、122° D、112°11. 在平面直角坐标系中,将点 做如下的连续平移,第 次向右平移得到点 , 第 次向下平移得到点 ,第 次向右平移得到点 ,第 次向下平移得到点 按此规律平移下去,则 的点坐标是( )A、 B、 C、 D、12. 如图, , , , , 给出以下结论: ; ; ; . 其中正确的结论有( )
A、132° B、128° C、122° D、112°11. 在平面直角坐标系中,将点 做如下的连续平移,第 次向右平移得到点 , 第 次向下平移得到点 ,第 次向右平移得到点 ,第 次向下平移得到点 按此规律平移下去,则 的点坐标是( )A、 B、 C、 D、12. 如图, , , , , 给出以下结论: ; ; ; . 其中正确的结论有( )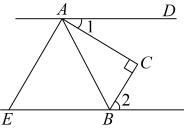 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本大题共6小题,每小题2分,共12分。)
-
13. 将“平行于同一条直线的两条直线平行”改写成“如果……那么……”的形式为.14. 如果 的平方根是±3,则 = .15. 小明和妈妈去电影院看电影,电影票上写着“9排12座”,小明学了有序数对后,把“9排12座”记作 , 那么妈妈的电影票“8排7座”记作 .16. 已知 为两个连续的整数,且 ,则 = .17. 已知直线过点 , 且与轴平行,直线过点 , 并与轴平行,则两直线的交点坐标是 .18. 如图,将一张长方形纸片沿折叠后,点D、C分别落在点、位置,的延长线与相交于点G,若 , .

三、解答题(共8题,共72分)
-
19. 计算:(1)、;(2)、 .20. 已知的平方根是 , 的立方根是2,c是的整数部分,求的算术平方根.21. 完成下面推理过程.
如图,已知∠1=∠2,∠B=∠C,可推得ABCD.理由如下:

∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换).
∴CEBF( ).
∴∠ ▲ =∠C( ).
又∵∠B=∠C(已知),
∴∠ ▲ =∠B(等量代换).
∴ABCD( ).
22. 如图,在平面直角坐标系xOy中,三角形三个顶点的坐标分别是 , 三角形ABC中任意一点 , 经平移后对应点为 , 将三角形作同样的平移得到三角形 , 点A,B,C的对应点分别为 . (1)、点的坐标为 , 点的坐标为 ;(2)、①画出三角形;
(1)、点的坐标为 , 点的坐标为 ;(2)、①画出三角形;②求出三角形的面积;
23. 如图,直线AB,CD相交于点O,OE平分∠BOD.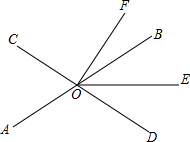 (1)、若∠EOF=55°,OD⊥OF,求∠AOC的度数;(2)、若OF平分∠COE,∠BOF=15°,求∠DOE的度数.24. 已知,如图,点F在AB上,点E在CD上,AE、DF分别交BC与H,G,∠A=∠D,∠FGB+∠EHG=180°.
(1)、若∠EOF=55°,OD⊥OF,求∠AOC的度数;(2)、若OF平分∠COE,∠BOF=15°,求∠DOE的度数.24. 已知,如图,点F在AB上,点E在CD上,AE、DF分别交BC与H,G,∠A=∠D,∠FGB+∠EHG=180°.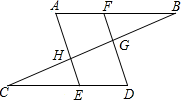 (1)、求证:AB∥CD;(2)、若AE⊥BC,直接写出图中所有与∠C互余的角,不需要证明.25.(1)、【问题发现】如图①,直线 , E是与之间的一点,连接 , 可以发现.
(1)、求证:AB∥CD;(2)、若AE⊥BC,直接写出图中所有与∠C互余的角,不需要证明.25.(1)、【问题发现】如图①,直线 , E是与之间的一点,连接 , 可以发现.


请把下面的证明过程补充完整:
证明:过点E作 ,
∵(已知),(辅助线的作法),
∴( ),
∴( ),
∵(作图),
∴ , ( ),
∴ (等量代换),即.
(2)、【拓展探究】如果点E运动到图②所示的位置,其他条件不变,进一步探究发现:之间的关系是.(3)、【解决问题】如图③, , 请求出的度数.26. 阅读材料,完成下列任务:因为无理数是无限不循环小数,因此无理数的小数部分我们不可能全部地写出来比如:、等,而常用的“…”或者“≈”的表示方法都不够百分百准确.
材料一:∵ , 即 ,
∴ .
∴的整数部分为1.
∴的小数部分为 .
材料二:我们还可以用以下方法求一个无理数的近似值.
我们知道面积是2的正方形的边长是 , 易知 , 因此可设 , 可画出如图示意图.由图中面积计算, , 另一方面由题意知 , 所以 .
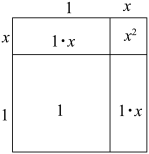
略去 , 得方程 , 解得 , 即 .
解决问题:
(1)、利用材料一中的方法,求的小数部分;(2)、利用材料二中的方法,探究的近似值.(画出示意图,标明数据,并写出求解过程)