2023-2024学年广西七年级下学期数学期中仿真模拟卷二
试卷更新日期:2024-04-14 类型:期中考试
一、单项选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中只有一项是符合要求的)
-
1. 平方根等于它本身的数是( )A、0 B、 C、1 D、2. 下列选项中,是无理数的是( )A、 B、3.14 C、 D、3. 如图,A,B,C,D中的哪幅图案可以通过图案①平移得到( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 如果P(m+3,2m+4)在y轴上,那么点P的坐标是( )A、(﹣2,0) B、(0,﹣2) C、(1,0) D、(0,1)5. 下列计算正确的是( )A、 B、 C、 D、6. 下列说法正确的是( )A、一定没有平方根 B、立方根等于它本身的数是 , C、的平方根是 D、的算数平方根是7. 如图,面积为5的正方形的顶点A在数轴上,且表示的数为 , 若点在数轴上,(点在点A的右侧)且 , 则点所表示的数为( )
4. 如果P(m+3,2m+4)在y轴上,那么点P的坐标是( )A、(﹣2,0) B、(0,﹣2) C、(1,0) D、(0,1)5. 下列计算正确的是( )A、 B、 C、 D、6. 下列说法正确的是( )A、一定没有平方根 B、立方根等于它本身的数是 , C、的平方根是 D、的算数平方根是7. 如图,面积为5的正方形的顶点A在数轴上,且表示的数为 , 若点在数轴上,(点在点A的右侧)且 , 则点所表示的数为( ) A、 B、 C、 D、8. 如图,将三个相同的三角尺不重叠无空隙地拼在一起,观察图形,在直线 BA,AC,CE,ED,CD,AE 中,相互平行的有( )
A、 B、 C、 D、8. 如图,将三个相同的三角尺不重叠无空隙地拼在一起,观察图形,在直线 BA,AC,CE,ED,CD,AE 中,相互平行的有( ) A、4组 B、3 组 C、2 组 D、1组9. 在平面直角坐标系中,将 , 沿着轴的负方向向下平移个单位后得到点.有四个点 , , , 一定在线段上的是( )A、点 B、点 C、点 D、点10. 如图,若∠3=∠4,则下列条件中,不能判定 AB∥CD的是( )
A、4组 B、3 组 C、2 组 D、1组9. 在平面直角坐标系中,将 , 沿着轴的负方向向下平移个单位后得到点.有四个点 , , , 一定在线段上的是( )A、点 B、点 C、点 D、点10. 如图,若∠3=∠4,则下列条件中,不能判定 AB∥CD的是( ) A、∠1=∠2 B、∠1=∠3 且∠2=∠4 C、∠1+∠3=90°且∠2+∠4=90° D、∠1+∠2=90°且∠3+∠4=90°11. 满足的整数有几个?( )A、3 B、4 C、5 D、612. 如图, , 将一副直角三角板作如下摆放, , . 下列结论:①;②;③;④ . 其中正确的个数是( )
A、∠1=∠2 B、∠1=∠3 且∠2=∠4 C、∠1+∠3=90°且∠2+∠4=90° D、∠1+∠2=90°且∠3+∠4=90°11. 满足的整数有几个?( )A、3 B、4 C、5 D、612. 如图, , 将一副直角三角板作如下摆放, , . 下列结论:①;②;③;④ . 其中正确的个数是( )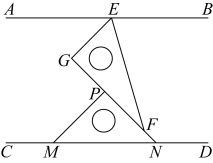 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(本大题共6小题,每小题2分,共12分。)
-
13. 如图,O对应的有序数对为(1,3)有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来或者翻译成中文为 .
 14. 请写出一个比﹣ 小的无理数:.15. 在平面直角坐标系中,点、 , , 若在平面直角坐标中存在一点 , 使得 , 且 , 则点的坐标为 .16. 一个正数的平方根是和 , 求这个正数 .17. 已知∠A与∠B的两边分别平行,其中∠B=(210-2x)°,则x的值为.18. 如图,将面积为5的正方形放在数轴上,以表示-1的点为圆心,以正方形的边长为半径作圆,交数轴于点 , 两点,则点 , 表示的数分别为 .
14. 请写出一个比﹣ 小的无理数:.15. 在平面直角坐标系中,点、 , , 若在平面直角坐标中存在一点 , 使得 , 且 , 则点的坐标为 .16. 一个正数的平方根是和 , 求这个正数 .17. 已知∠A与∠B的两边分别平行,其中∠B=(210-2x)°,则x的值为.18. 如图,将面积为5的正方形放在数轴上,以表示-1的点为圆心,以正方形的边长为半径作圆,交数轴于点 , 两点,则点 , 表示的数分别为 .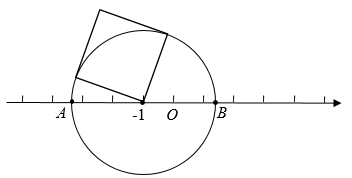
三、解答题(共8题,共72分)
-
19. 计算:20. 已知:和是的两个不同的平方根,是的立方根求、、的值.21. 如图,FG∥CD,∠1=∠3,∠B=60°,求∠BDE的度数.
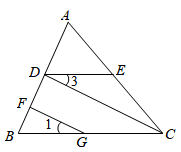
请把下面的解答过程补充完整.
解:∵FG∥CD(已知),
∴∠1= ▲ ( ).
又∵∠1=∠3(已知),
∴∠3= ▲ (等量代换),
∴BC∥ ▲ ( ),
( )
又∵∠B=60°(已知),
∴∠BDE= ▲ °(等式的性质).
22. 如图,在平面直角坐标系中, , , . 将三角形向左平移5个单位长度,再向上平移3个单位长度,可以得到三角形 , 其中点 , , 分别与点 , , 对应. (1)、画出平移后的三角形;(2)、直接写出 , , 三个点的坐标;(3)、若点在轴上,以 , , 为顶点的三角形面积为2,求点的坐标.23. 如图,点在直线上, , .
(1)、画出平移后的三角形;(2)、直接写出 , , 三个点的坐标;(3)、若点在轴上,以 , , 为顶点的三角形面积为2,求点的坐标.23. 如图,点在直线上, , . (1)、若 , 求的度数;(2)、试猜想和的数量关系,请直接写出结果 .24. 将一副三角板中的两个直角顶点叠放在一起如图 , 其中 , , .
(1)、若 , 求的度数;(2)、试猜想和的数量关系,请直接写出结果 .24. 将一副三角板中的两个直角顶点叠放在一起如图 , 其中 , , .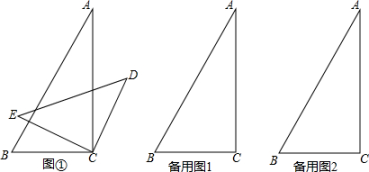 (1)、若 , 求的度数;(2)、试猜想与的数量关系,请说明理由;(3)、若按住三角板不动,绕顶点转动三角板 , 试探究等于多少度时, , 并简要说明理由.25. 【阅读思考】如图①,已知 , 探究、、之间关系,小明添加了一条辅助线.解决了这道题.得到的结果是 .
(1)、若 , 求的度数;(2)、试猜想与的数量关系,请说明理由;(3)、若按住三角板不动,绕顶点转动三角板 , 试探究等于多少度时, , 并简要说明理由.25. 【阅读思考】如图①,已知 , 探究、、之间关系,小明添加了一条辅助线.解决了这道题.得到的结果是 .证明过程如下:
如图①,过点作
.
,
,
,
, 即 .
 (1)、【理解应用】如图②,已知 , 求的度数;(2)、【拓展探索】如图③,已知 , 点在点的右侧, , 平分 , 平分 , , 所在的直线交于点 , 点在直线与之间,点在点的右侧,且 , , 若 , 则度数为?(用含的代数式表示)26. 【阅读材料】
(1)、【理解应用】如图②,已知 , 求的度数;(2)、【拓展探索】如图③,已知 , 点在点的右侧, , 平分 , 平分 , , 所在的直线交于点 , 点在直线与之间,点在点的右侧,且 , , 若 , 则度数为?(用含的代数式表示)26. 【阅读材料】∵ , 即 ,
∴的整数部分为3,
∵一个数字是由整数部分和小数部分相加而成,
∴一个数字的小数部分=这个数字-它的整数部分,
∴的小数部分为 .
【解决问题】
(1)、填空:的小数部分是 .(2)、已知m是的整数部分,n是的小数部分,求代数式的立方根.