2023-2024学年广西七年级下学期数学期中仿真模拟卷一

试卷更新日期：2024-04-14 类型：期中考试

进入出卷网下载

一、单项选择题（本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中只有一项是符合要求的)

1. 9的算术平方根是（）

A、 $3$ B、 $- 3$ C、 $\pm 3$ D、 $\pm \sqrt{3}$

查看试题解析
2. 在 $\frac{22}{7} ， \frac{2 π}{3} ， \sqrt{2} ， - \sqrt{3} ， \sqrt[3]{- 8} ， - \sqrt{16}$ ， 3.14，0.5757757775……（相邻两个5之间7的个数逐次加1）中，无理数的个数为（　　）

A、2 B、3 C、4 D、5

查看试题解析
3. 下列图案中，可以看作是由图案自身的一部分经平移后得到的是（）

A、 B、 C、 D、

查看试题解析
4. 在平面直角坐标系中，点 $(m ， n)$ 位于第三象限，则（）

A、 $m < n$ B、 $m > n$ C、 $m n > 0$ D、 $m + n > 0$

查看试题解析
5. 面积为 2 的正方形的边长是（）

A、2的平方根 B、2的算术平方根 C、2开平方的结果 D、2的立方根

查看试题解析
6. 一个数的平方根与立方根相等，则这个数是（）

A、 $0$ B、 $1$ C、 $- 1$ D、 $0$ 或 $- 1$ 或 $1$

查看试题解析
7. 如图，估计 $\sqrt{7}$ 的值所对应的点可能落在（）

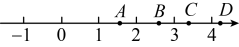A、点A处 B、点B处 C、点C处 D、点D处

查看试题解析
8. 如图，下列条件中，能判定AB∥EF的是（）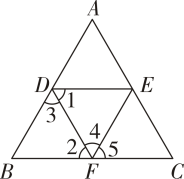
①∠B+∠BFE=180°；
②∠1=∠2；
③∠3=∠4；
④∠B=∠5.

A、② B、①③ C、①③④ D、②③④

查看试题解析
9. 平面直角坐标系中，将点 $P (a ， b)$ 向左平移 $1$ 个单位长度再向上平移 $2$ 个单位长度得到的点的坐标是（）

A、 $(a + 1 ， b + 2)$ B、 $(a + 1 ， b - 2)$ C、 $(a - 1 ， b + 2)$ D、 $(a - 1 ， b - 2)$

查看试题解析
10. 如图，小丽的奶奶家在A点的正北方向C处，但需要走一条弯的路才能到达，小丽先沿北偏东 $57 °$ 走了一段距离后，转弯沿北偏西 $33 °$ 再走一段距离即可走到奶奶家，则转弯处∠ABC的度数为（　　）

A、 $33 °$ B、 $57 °$ C、 $90 °$ D、 $100 °$

查看试题解析
11. 比较2， $\sqrt{5}$ ， $\sqrt[3]{7}$ 的大小，正确的是（）

A、2< $\sqrt{5}$ < $\sqrt[3]{7}$ B、2< $\sqrt[3]{7}$ < $\sqrt{5}$ C、 $\sqrt[3]{7}$ <2< $\sqrt{5}$ D、 $\sqrt{5}$ < $\sqrt[3]{7}$ <2

查看试题解析
12. 如图，已知直线AB，CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB，CD，AC上），设∠BAE=α，∠DCE=β．下列各式：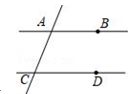

①α+β，②α﹣β，③β﹣α，④360°﹣α﹣β，∠AEC的度数可能是（）

A、①②③ B、①②④ C、①③④ D、①②③④ 图4

查看试题解析

二、填空题（每题2分，共12分）

13. 七年级三班座位按7排8列排列，王东的座位是3排4列，简记为（3，4），张三的座位是5排2列，可简记为．

查看试题解析
14. $m 、 n$ 是连续的两个整数，若 $m < \sqrt{6} < n$ ，则 $m + n$ 的值为．

查看试题解析
15. 已知点A(m﹣1，m+4)在y轴上，则点A的坐标是.

查看试题解析
16. 依据图中呈现的运算关系，可知 $m + n =$ ．

查看试题解析
17. 如图，半径为 $1$ 个单位长度的圆沿数轴从实数 $- 1$ 对应的点向右滚动一周，圆上的 $A$ 点恰好与点 $B$ 重合，则点 $B$ 对应的实数是．

查看试题解析
18. 一副直角三角尺如图①叠放，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动，要求两块三角尺的一组边互相平行.如图②，当∠BAD=15°时，有一组边BC∥DE，请再写出两个符合要求的∠BAD（0°＜∠BAD＜180°）的度数.

查看试题解析

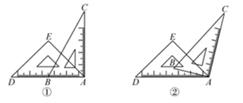
三、解答题（共8题，共72分）

19. 计算：

(1)、 $\sqrt[3]{- 64} + \sqrt{25}$ ；

(2)、 $2 \times (3 + \sqrt{5}) + 4 - 2 \sqrt{5}$ ．

查看试题解析
20. 已知：x﹣2的平方根是±2，2x+y+7的立方根是3，求x²+y²的算术平方根．

查看试题解析
21. 填空：如图，AB⊥BC，BC⊥CD，且∠1=∠2，试说明：BE∥CF.
解：∵AB⊥BC，BC⊥CD（已知），
∴     ▲        =    ▲        =90°（         ）.
又∵∠1=∠2（已知），
∴     ▲        =    ▲        （等式的性质），
∴BE∥CF（                   ）.

查看试题解析
22. 如图， $Δ A B C$ 的三个顶点 $A$ 、 $B$ 、 $C$ 都在小正方格的格点上，现将 $Δ A B C$ 向左平移5个单位，得到 $Δ A_{1} B_{1} C_{1}$ .

(1)、画出平移后的 $Δ A_{1} B_{1} C_{1}$ （点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 分别是 $A$ 、 $B$ 、 $C$ 的对应点）；

(2)、写出 $A_{1}$ 、 $B_{1}$ 两点的坐标；

(3)、计算 $Δ A_{1} B_{1} C_{1}$ 的面积；

(4)、在图中连接 $A A_{1}$ 和 $C C_{1}$ ，则这两条线段之间有什么关系？直接回答（不需要说理由）.

查看试题解析
23. 如图，直线AB，CD相交于点O，EO⊥AB，垂足为O．

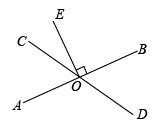(1)、若∠EOC＝35°，求∠AOD的度数；

(2)、若∠BOC＝2∠AOC，求∠DOE的度数．

查看试题解析
24. 如图，已知 $B C ∥ G E$ ， $A F ∥ D E$ ， $∠ 1 = 50 °$ .

(1)、求 $∠ A F G$ 的度数；

(2)、若 $A Q$ 平分 $∠ F A C$ ，交 $B C$ 于点 $Q$ ，且 $∠ Q = 15 °$ ，求 $∠ A C B$ 的度数.

查看试题解析
25. 阅读资料：在学习平行线知识的时候，小敏同学发现有的图形（如图1），不属于两条平行线被第三条直线所截的图形，不能直接应用平行线的性质解决问题．经过思考，小敏想到，若过点C作CF∥AB（如图2），这样就多了一个已知条件，问题就可以解决了．
请你参考小敏同学的方法，解决下面问题：

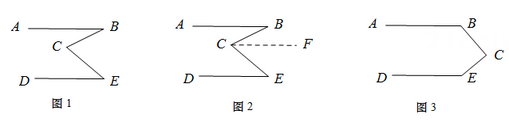(1)、如图2，已知AB∥DE，用等式表示∠B，∠E，∠BCE之间的数量关系，并说明理由．

(2)、如图3，已知AB∥DE，直接用等式表示出∠B，∠E，∠BCE之间的数量关系．

查看试题解析
26. 【阅读材料】：∵ $2 < \sqrt{5} < 3$ ， ∴ $\sqrt{5}$ 的整数部分为2， $\sqrt{5}$ 的小数部分为 $\sqrt{5} - 2$ .
【解决问题】：

(1)、填空： $\sqrt{91}$ 的小数部分是；

(2)、已知 $a$ 是 $\sqrt{21} - 4$ 的整数部分， $b$ 是 $\sqrt{21} - 4$ 的小数部分，求代数式 ${(- a)}^{3} + {(b + 4)}^{2}$ 的值；

(3)、已知： $x$ 是 $3 + \sqrt{5}$ 的整数部分， $y$ 是其小数部分，请直接写出 $x - y$ 的相反数.

查看试题解析