2024年北师大版数学八年级下册周测卷（第六章第3-4节）基础卷
试卷更新日期：2024-04-14 类型：同步测试
一、选择题（每题3分，共30分）
-
1. 如图，两点被池塘隔开，三点不共线．设的中点分别为 ． 若米，则（ ）
A、4米 B、6米 C、8米 D、10米2. 如图，在△ABC中，点D，E，F分别是AB，AC，BC的中点，已知∠ADE=65°，则∠CFE的度数为（ ）
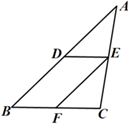A、60° B、65° C、70° D、75°3. 一个七边形的内角和是（ ）A、 B、 C、 D、4. 如图，将三角形纸片剪掉一角得四边形，设△ABC与四边形BCDE的外角和的度数分别为 ， ，则正确的是（ ）
A、 B、 C、 D、无法比较 与 的大小5. 如图，小明从点A出发沿直线前进10米到达点B，向左转 后又沿直线前进10米到达点C，再向左转 后沿直线前进10米到达点D……照这样走下去，小明第一次回到出发点A时所走的路程为（ ）
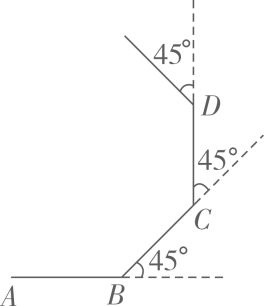A、100米 B、80米 C、60米 D、40米6. 将含30°角的一个直角三角板和一把直尺如图放置，若 ，则 等于（ ）
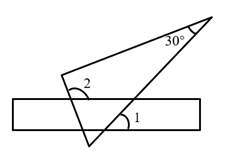A、80° B、100° C、110° D、120°7. 如图平行四边形中，对角线相交于点 ， 点E是的中点，若 ， 则的长为（ ）
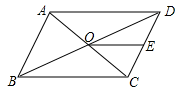A、3 B、12 C、8 D、108. 如图，是的中线，E、F分别是 ， 的中点，连结 ． 若 ， 则的长为（ ）
A、4 B、3 C、6 D、59. 如图，任意四边形各边中点分别是、、、若对角线、的长分别是、 ， 则四边形的周长是（ ）
A、 B、 C、 D、10. 如图，在▱中， ， 为上一点， ， 分别为 ， 的中点，则的长为（ ）
A、 B、 C、 D、不确定二、填空题（每题3分，共18分）
-
11. 如图，在矩形中，点 ， 分别为 ， 的中点，若 ， 则的长为 ．
12. 如图，在中，、分别是、的中点， ， 则长为 ．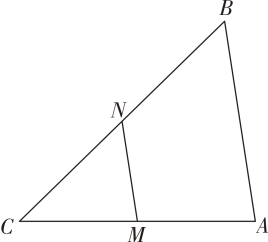
13. 如图，在中， ， 为上一点，M ， N分别为 ， 的中点，则的长为 ．
14. 一个n边形的每个外角都等于36°，则n=.15. 如图，在五边形ABCDE中，∠1+∠2+∠3+∠4+∠5=°.
16. 如图，在正五边形ABCDE中，以AB为一边，在正五边形内作正方形ABMN，则∠CBM=°.
三、解答题（共7题，共72分）
-
17. 如图，某游乐场的游客中心位于处，其正南方向处有海盗船游乐项目 ， 在海盗船游乐项目的正东方向处是摩天轮游乐项目 ， 餐厅位于的中点处；碰碰车游乐项目位于的中点处．小乐和曼曼同时从处出发，小乐经处到处匀速游玩，曼曼先沿路线匀速游玩到餐厅 ， 后又沿南偏西方向的路线匀速直线游玩．曼曼全程与小乐的游玩速度相同．
(1)、餐厅和碰碰车游乐项目的距离是；(2)、若小乐在由到游玩途中与曼曼相遇于处，求相遇处到海盗船游乐项目的距离．18. 如图，四边形ABCD中，∠BAD＝106°，∠BCD＝64°，点M，N分别在AB，BC上，得 FMN，若MF∥AD，FN∥DC.
求：
(1)、∠F的度数；(2)、∠D的度数.19. 如图，在▱ABCD中，E，F分别是AD，BC边上的点，且DE=CF，BE和AF的交点为M，CE和DF的交点为N，连接MN，EF.
(1)、求证：四边形ABFE为平行四边形；(2)、若AD=6cm，求MN的长.20. 如图，在△ABC中，AB＝13，AC＝23，点D在AC上，若BD＝CD＝10，AE平分∠BAC ．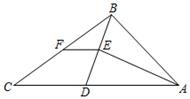
(1)、求AE的长；(2)、若F是BC中点，求线段EF的长．21. 如图，在ABCD中，点G，H分别是AB，CD的中点，点E，F在对角线AC上， 且AE=CF．
(1)、求证：四边形EGFH是平行四边形；(2)、连结BD交AC于点O，若BD= 10，AE+CF=EF ，求EG的长．
