2024年北师大版数学八（下）微素养核心突破7 因式分解的应用

试卷更新日期：2024-04-14 类型：复习试卷

进入出卷网下载

一、选择题

1. 已知ab＝2，a-2b＝3，则4ab²-2a²b的值是（）

A、6 B、-6 C、12 D、-12

查看试题解析
2. 已知a，b，c分别是△ABC的三边长，若 $a^{2} + 2 a b + b^{2} = c^{2} + 24$ ， $a + b - c = 4$ ，则△ABC的周长是（）

A、3 B、6 C、8 D、12

查看试题解析
3. 已知 $a$ 、 $b$ 、是三角形的三条边，那么代数式 ${(a - b)}^{2} - c^{2}$ 的值（）

A、大于0 B、等于0 C、小于0 D、无法确定

查看试题解析
4. 已知 $2 x - y = 1$ ， $x y = 2$ ，则 $4 x^{3} y - 4 x^{2} y^{2} + x y^{3}$ 的值为（）

A、-2 B、1 C、-1 D、2

查看试题解析
5. 如图，边长为a、b的长方形周长为20，面积为16，则a²b+ab²的值为（）

A、80 B、160 C、320 D、480

查看试题解析
6. 利用因式分解计算：3²⁰²²﹣3²⁰²¹的结果为（）

A、2×3²⁰²¹ B、1 C、3 D、3²⁰²¹

查看试题解析
7. 小明是一位密码编译爱好者，在他的密码手册中，有这样一条信息： $x - y$ ，a-b，5， $x^{2} - y^{2}$ ，a， $x + y$ ， $a^{2} - a b$ 分别对应下列七个字：会、城、我、美、爱、运、丽，现将 $5 a^{2} (x^{2} - y^{2}) - 5 a b (x^{2} - y^{2})$ 因式分解，分解结果经密码翻译呈现准确的信息是（）

A、我爱美丽城 B、我爱城运会 C、城运会我爱 D、我美城运会

查看试题解析
8. 我们把被分解的多项式分成若干组，分别按“基本方法”即提取公因式法和运用公成法进行分解，然后，综合起来，再从总体上按“基本方法”继续进行分解，直到分解出最后结果，这种分解因式的方法叫做分组分解法.例如： $m^{2} + n^{2} - 2 m n + n - m = (m^{2} - 2 m n + n^{2})$ $- (m - n) = (m - n)^{2} - (m - n) = (m - n) (m - n - 1)$ ，根据上述方法，解决问题：已知a、b、c是△ABC的三边，且满足 $a^{2} - b^{2} + a c - b c = 0$ ，则△ABC的形状是（）

A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形

查看试题解析

二、填空题

9. 因式分解：2xy+9﹣x²﹣y²＝．
利用因式分解计算：（﹣2）²⁰²²+（﹣2）²⁰²¹﹣2²⁰²⁰＝．

查看试题解析
10. 数3⁴⁸﹣1能被30以内的两位数（偶数）整除，这个数是．

查看试题解析
11. 某工人师傅要制作一个底面为正方形的无盖长方体盒子，他在一块边长为a的正方形铁皮的四个角，各剪去一个边长为b（ $a > b$ ），如图所示，若 $a = 3.6$ ， $b = 0.8$ ，则剩余部分的面积是．

查看试题解析
12. 若一个四位数 $M$ 的个位数字与十位数字的和与它们的差之积恰好是 $M$ 去掉个位数字与十位数字后得到的两位数，则这个四位数 $M$ 称为“和差数”，令 $M$ 的千位数字为 $a$ ，百位数字为 $b$ ，十位数字为 $c$ ，个位数字为 $d$ ，记 $G (M) = \frac{d}{c}$ ，且 $P (M) = \frac{M}{c + d}$ ，则 $\frac{G (1224)}{P (1224)} =$ ；当 $G (M)$ ， $P (M)$ 均为整数时， $M$ 的最大值为．

查看试题解析
13. 对于一个各数位上的数字均不为0的三位自然数N，若N能被它的各数位上的数字之和m整除，则称N是m的“整倍数”．例如：∵ $135 \div (1 + 3 + 5) = 135 \div 9 = 15$ ， ∴135是9的“整倍数”，又如∵ $524 \div (5 + 2 + 4) = 524 \div 11 = 47 ⋯ ⋯ 7$ ∴524不是11的“整倍数”．三位数A是12的“整倍数”，a，b，c分别是数A其中一个数位上的数字，且 $c < b < a$ ．在a，b，c中任选两个组成两位数，其中最大的两位数记为 $P (A)$ ，最小的两位数记为 $Q (A)$ ，若 $\frac{P (A) + Q (A)}{16}$ 为整数，求出满足条件的数A的最小值为．

查看试题解析
14. 如图

(1)、如图1，现有编号为①②③④的四种长方体各若干块，现取其中两块拼成一个大长方体如图2，据此写出一个多项式的因式分解：．

(2)、若要用这四种长方体拼成一个棱长为 $(x + 1)$ 的正方体，需要②号长方体个，③号长方体个，据此写出一个多项式的因式分解：．

查看试题解析

三、综合题

15. 对于任意两个数a、b的大小比较，有下面的方法：当 $a - b > 0$ 时，一定有 $a > b$ ；当 $a - b = 0$ 时，一定有 $a = b$ ；当 $a - b < 0$ 时，一定有 $a < b$ ．反过来也成立．因此，我们把这种比较两个数大小的方法叫做“求差法”．请根据以上材料完成下面的题目：

(1)、已知： $A = 2 x^{2} y + 8 y$ ， $B = 8 x y$ ，且 $A > B$ ，试判断y的符号；

(2)、已知：a、b、c为三角形的三边，比较 $a^{2} + c^{2} - b^{2}$ 和 $2 a c$ 的大小．

查看试题解析
16. 我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释，例如：图1可以用来解释 $a^{2} + 2 a b + b^{2} = (a + b)^{2}$ ．现有足够多的正方形卡片1号、2号，长方形卡片3号，如图3.

(1)、根据图2完成因式分解： $2 a^{2} + 2 a b =$ ；

(2)、现有1号卡片1张、2号卡片4张，3号卡片4张，在不重叠的情况下可以紧密地拼成一个大正方形，则这个大正方形的边长为；（用含 $a ､ b$ 的式子表示）

(3)、图1中的1号和2号卡片所占面积之和为 $S_{1}$ ，两个3号卡片所占面积之和为 $S_{2}$ ，求证： $S_{1} - S_{2} ⩾ 0$ ．

查看试题解析
17. 有些多项式的某些项可以通过适当地结合，（或把某项适当地拆分）成为一组，利用分组来分解多项式的因式，从而达到因式分解的目的，例如将 $x^{2} - 4 y^{2} - 2 x + 4 y$ 因式分解。
原式 $= x^{2} - 4 y^{2} - 2 x + 4 y = (x + 2 y) (x - 2 y) - 2 (x - 2 y) = (x - 2 y) (x + 2 y - 2)$ 。
请在这种方法的启发下，解决以下问题：

(1)、分解因式 $x^{2} + x - 5 x - 5$ ；

(2)、 $△ A B C$ 三边 $a$ ， $b$ ， $c$ 满足 $a^{2} + a b + c^{2} - b c = 2 a c$ ，判断 $△ A B C$ 的形状，并说明理由。

(3)、“赵爽弦图”是由四个全等的直角三角形围成的一个大正方形，中间是一个小正方形。若直角三角形的两条直角边长分别是 $a$ 和 $b (a > b)$ ，斜边长是4，小正方形的面积是1。根据以上信息，先将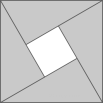 $a^{4} - 2 a^{3} b + 2 a^{2} b^{2} - 2 a b^{3} + b^{4}$ 因式分解，再求值。

查看试题解析
18. 在现今“互联网＋”的时代，密码与我们的生活已经密不可分．而诸如“123456”、生日等简单密码又容易被破解，因此利用简单方法产生一组容易记忆的密码就很有必要了．有一种用“因式分解”法产生的密码，方便记忆，其原理是：将一个多项式分解因式，如多项式： $x^{3} + 2 x^{2} - x - 2$ 因式分解的结果为 $(x - 1) (x + 1) (x + 2)$ ，当 $x = 18$ 时， $x - 1 = 17$ ， $x + 1 = 19$ ， $x + 2 = 20$ ，此时可以得到六位数的数字密码171920．

(1)、根据上述方法，当 $x = 21$ ， $y = 7$ 时，对于多项式 $x^{3} - x y^{2}$ 分解因式后可以形成哪些数字密码（写出三个）

(2)、若一个直角三角形的周长是30，斜边长为13，其中两条直角边分别为x、y，求出一个由多项式 $x^{3} y + x y^{3}$ 分解因式后得到的六位数的数字密码（只需一个即可）；

(3)、若多项式 $x^{3} + (m - 3 n) x^{2} - n x - 21$ 因式分解后，利用本题的方法，当 $x = 27$ 时可以得到其中一个六位数的数字密码为242834，求m、n的值．

查看试题解析

四、实践探究题

19. 常用的分解因式的方法有提取公因式法、公式法及到了高中还要学习的十字相乘法，但有更多的多项式只用上述方法就无法分解，如 $x^{2} - 4 y^{2} - 2 x + 4 y$ ，我们细心观察这个式子就会发现，前两项符合平方差公式，后两项可提取公因式，前后两部分分别分解因式后会产生公因式，然后提取公因式就可以完成整个式子的分解因式了．过程为：
$x^{2} - 4 y^{2} - 2 x + 4 y = (x + 2 y) (x - 2 y) - 2 (x - 2 y) = (x - 2 y) (x + 2 y - 2)$

这种分解因式的方法叫分组分解法．利用这种方法解决下列问题：

(1)、分解因式 $a^{2} - 4 a - b^{2} + 4$ ；

(2)、 $△ A B C$ 三边 $a ， b ， c$ 满足 $a^{2} - a b - a c + b c = 0$ ，判断 $△ A B C$ 的形状．

查看试题解析
20. 把代数式通过配凑等手段，得到局部完全平方式，再进行有关运算和解题，这种解题方法叫做配方法．如：
①用配方法分解因式： $a ² + 4 a + 3$ ．

解：原式： $= a ² + 4 a + 4 - 1 = (a + 2) ² - 1 = (a + 2 + 1) (a + 2 - 1) = (a + 3) (a + 1)$

② $M = 2 a^{2} - 4 a + 6$ ，利用配方法求M的最小值．

解： $M = 2 a^{2} - 4 a + 6 = 2 (a^{2} - 2 a + 1) + 6 - 2 = 2 (a - 1)^{2} + 4$

$∵ 2 (a - 1)^{2} \geq 0 ， ∴ 2 (a - 1)^{2} + 4 \geq 4 ，$

∴当 $a = 1$ 时，M有最小值4．

请根据上述材料解决下列问题：

(1)、用配方法因式分解 $x ² - 4 x - 12$ ；

(2)、若 $M = 4 x^{2} + 4 x - 1$ ，求M的最小值．

查看试题解析
21. 我们把多项式 $a^{2} + 2 a b + b^{2}$ 及 $a^{2} - 2 a b + b^{2}$ 叫做完全平方式．如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些非负数有关的问题或求代数式最大值、最小值等．
例如：分解因式 $x^{2} + 2 x - 3 = (x^{2} + 2 x + 1) - 4 = {(x + 1)}^{2} - 4 = (x + 1 + 2) (x + 1 - 2) = (x + 3) (x - 1)$ ；例如求代数式 $2 x^{2} + 4 x - 6$ 的最小值．由 $2 x^{2} + 4 x - 6 = 2 (x^{2} + 2 x + 1 - 1) - 6 = 2 {(x + 1)}^{2} - 8$ 可知，当 $x = - 1$ 时， $2 x^{2} + 4 x - 6$ 有最小值，最小值是 $- 8$ ．
根据阅读材料用配方法解决下列问题；

(1)、分解因式： $m^{2} - 4 m - 5 =$ ；

(2)、当a，b为何值时，多项式 $a^{2} + b^{2} - 4 a + 6 b + 18$ 有最小值，并求出这个最小值；

(3)、当a，b为何值时，多项式 $a^{2} - 2 a b + 2 b^{2} - 2 a - 4 b + 27$ 有最小值，并求出这个最小值．

查看试题解析
22. 我们来规定下面两种数：
①平方和数：若一个三位或者三位以上的正整数分成左、中、右三个数后满足：中间数＝（左边数）²+（右边数）² ，我们就称该整数是平方和数，例如：整数 $251$ ，它的中间数是5，左边数是2，右边数是1，∵ $2^{2} + 1^{2} = 5$ ， ∴ $251$ 是平方和数；再例如： $3254$ ， ∵ $3^{2} + 4^{2} = 25$ ， ∴ $3254$ 是一个平方和数；当然152， $4253$ 这两个数也肯定是平方和数；
②双倍积数：若一个三位或者三位以上的正整数分成左、中、右三个数后满足：中间数＝2×左边数×右边数，我们称该整数是双倍积数；例如：整数 $142$ ，它的中间数是4，左边数是1，右边数是2，∵ $2 \times 1 \times 2 = 4$ ， ∴ $142$ 是一个双倍积数；再例如： $3305$ ， ∵ $2 \times 3 \times 5 = 30$ ， ∴ $3305$ 是一个双倍积数；当然， $241$ ， $5303$ 也是一个双倍积数；
注意：在下列问题中，我们统一用字母a表示一个正整数分出来的左边数，用字母b表示一个正整数分出来的右边数，请根据上述定义完成下面问题：

(1)、如果一个三位正整数为平方和数，且十位数字是4，则该三位整数是；如果一个三位正整数为双倍积数，十位数字是8，则该三位整数是；

(2)、若一个正整数既是平方和数，又是双倍积数，试探究a、b的数量关系，并说明理由；

(3)、若正整数 $a 1125 b$ 为一个平方和数， $a 900 b$ 为一个双倍积数，求 $a^{2} - b^{2} + 2 b - 1$ 的值．

查看试题解析