2024年北师大版数学八(下)微素养核心突破5 平移与旋转的相关综合题
试卷更新日期:2024-04-14 类型:复习试卷
一、选择题
-
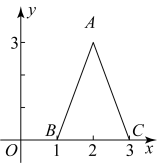
1. 如图,面积为3的等腰 , , 点B、点C在x轴上,且、C , 规定把 “先沿y轴翻折,再向下平移1个单位”为一次变换,这样连续经过2023次变换后,顶点A的坐标为( )
 A、 B、 C、 D、2. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点;下列结论:①;②平分;③ , 其中所有正确结论的序号是( )
A、 B、 C、 D、2. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点;下列结论:①;②平分;③ , 其中所有正确结论的序号是( ) A、①② B、②③ C、①③ D、①②③3. 如图,边长为6的等边三角形中,E是对称轴上一个动点,连接 , 将线段绕点C逆时针旋转60度得到 , 连接 , 则在点E运的过程中,最小值是( )
A、①② B、②③ C、①③ D、①②③3. 如图,边长为6的等边三角形中,E是对称轴上一个动点,连接 , 将线段绕点C逆时针旋转60度得到 , 连接 , 则在点E运的过程中,最小值是( ) A、 B、2 C、 D、4. 如图,已知△ABC绕点A逆时针旋转a(0<a<∠BAC)得到△ADF,AB=AC,AD交BC于点F,DE交BC、AC于点G、H,则以下结论:①△ABF≌△AEH:②FG=CC:③连接AG、FH,则AG⊥FH:④当DF的长度最大时,AD平分∠BAC.其中正确的结论有( )
A、 B、2 C、 D、4. 如图,已知△ABC绕点A逆时针旋转a(0<a<∠BAC)得到△ADF,AB=AC,AD交BC于点F,DE交BC、AC于点G、H,则以下结论:①△ABF≌△AEH:②FG=CC:③连接AG、FH,则AG⊥FH:④当DF的长度最大时,AD平分∠BAC.其中正确的结论有( )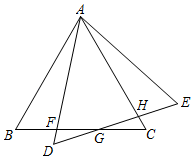 A、1个 B、2个 C、3个 D、4个5. 如图,在中, , P是上一动点,将点P绕点逆时针旋转落在点处,当点落在边上时,点的坐标为( )
A、1个 B、2个 C、3个 D、4个5. 如图,在中, , P是上一动点,将点P绕点逆时针旋转落在点处,当点落在边上时,点的坐标为( )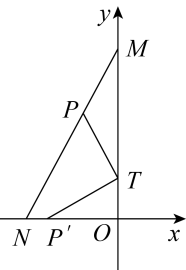 A、 B、 C、 D、6. 如图,已知A(3,1)与B(1,0),PQ是直线 上的一条动线段且 (Q在P的下方),当AP+PQ+QB最小时,Q点坐标为( )
A、 B、 C、 D、6. 如图,已知A(3,1)与B(1,0),PQ是直线 上的一条动线段且 (Q在P的下方),当AP+PQ+QB最小时,Q点坐标为( )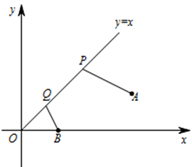 A、( , ) B、( , ) C、(0,0) D、(1,1)
A、( , ) B、( , ) C、(0,0) D、(1,1)二、填空题
-
7. 如图,在中, , 将绕点顺时针旋转,使点落在斜边上的点处,连接 , 则=°.
 8. 如图,点P是等边三角形内的一点,且 , , , 则的度数为 .
8. 如图,点P是等边三角形内的一点,且 , , , 则的度数为 . 9. 如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.在旋转过程中,当∠ADM=90时,则AM的长为 , 若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2 , 如图2,此时∠AD2C=135°,CD2=60,则BD2的长为 .
9. 如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.在旋转过程中,当∠ADM=90时,则AM的长为 , 若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2 , 如图2,此时∠AD2C=135°,CD2=60,则BD2的长为 .
 10. 如图,在中, , 将绕点B按逆时针方向旋转α度得到 . 若点刚好落在边上,则 .
10. 如图,在中, , 将绕点B按逆时针方向旋转α度得到 . 若点刚好落在边上,则 . 11. 如图,在中, , , , 将绕点B逆时针旋转至 , 连接 , 则线段 .
11. 如图,在中, , , , 将绕点B逆时针旋转至 , 连接 , 则线段 . 12. 如图,已知在等腰直角△ABC中,∠ACB=90°,AC=BC,点D在线段AB上,△CBD绕着点C顺时针方向旋转90°后得到△CAE,点B和点D的对应点分别是点A和点E,点M在线段AB上,且△CEM与△CDM恰好关于直线CM成轴对称,如果AM:MD:DB=3:5:4,△ABC的面积为24,那么△AME的面积为 .
12. 如图,已知在等腰直角△ABC中,∠ACB=90°,AC=BC,点D在线段AB上,△CBD绕着点C顺时针方向旋转90°后得到△CAE,点B和点D的对应点分别是点A和点E,点M在线段AB上,且△CEM与△CDM恰好关于直线CM成轴对称,如果AM:MD:DB=3:5:4,△ABC的面积为24,那么△AME的面积为 .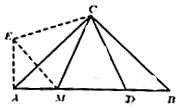 13. 如图,等边三角形ABC的顶点A、B坐标分别为(1,1)和(3,1),规定将等边三角形ABC先沿x轴翻折,再向左平移1个单位为第一次变换,则这样连续经过2021次变换后,等边三角形ABC的顶点C的坐标为 .
13. 如图,等边三角形ABC的顶点A、B坐标分别为(1,1)和(3,1),规定将等边三角形ABC先沿x轴翻折,再向左平移1个单位为第一次变换,则这样连续经过2021次变换后,等边三角形ABC的顶点C的坐标为 .
三、作图题
-
14. 如图,在平面直角坐标系中,点A的坐标为 , 点与点A关于轴对称,点先向右平移4个单位长度,再向上平移2个单位长度得到点 .
 (1)、描出点和点 , 并依次连接、、 , 得到;(2)、将(1)中的的各顶点的横坐标和纵坐标都乘 , 得到点的对应点 , 点的对应点 , 点的对应点 , 在平面直角坐标系中描出点、、 , 并依次连接、、 , 得到;(3)、在(2)的条件下, .15. 如图,已知 , , 是平面直角坐标系上三点.
(1)、描出点和点 , 并依次连接、、 , 得到;(2)、将(1)中的的各顶点的横坐标和纵坐标都乘 , 得到点的对应点 , 点的对应点 , 点的对应点 , 在平面直角坐标系中描出点、、 , 并依次连接、、 , 得到;(3)、在(2)的条件下, .15. 如图,已知 , , 是平面直角坐标系上三点.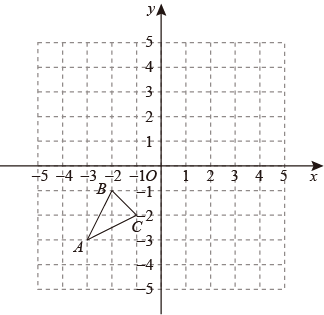 (1)、请画出关于y轴对称的(2)、请画出向上平移4个单位,向右平移5个单位得到的;(3)、如果将各顶点的横坐标和纵坐标都乘2,所得到的三角形和原三角形的形状和大小有什么关系?(4)、在x轴上找一点E,使最小(保留作图痕迹),并求出这个最小距离的值.
(1)、请画出关于y轴对称的(2)、请画出向上平移4个单位,向右平移5个单位得到的;(3)、如果将各顶点的横坐标和纵坐标都乘2,所得到的三角形和原三角形的形状和大小有什么关系?(4)、在x轴上找一点E,使最小(保留作图痕迹),并求出这个最小距离的值.四、综合题
-
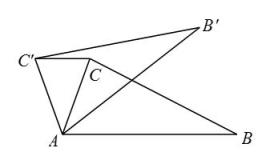
16. 如图,在中, , 在同一平面内,将绕点逆时针旋转到的位置,连接 , 求证:.
 17. 阅读下面材料,并解决问题:
17. 阅读下面材料,并解决问题: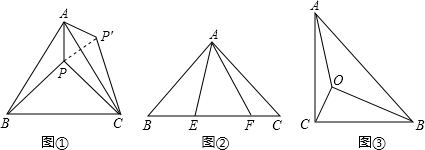 (1)、如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
(1)、如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=;
(2)、基本运用请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)、能力提升如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
18. 阅读情境:在综合实践课上,同学们探究“全等的等腰直角三角形图形变化问题”.如图1, , 其中 , , 此时,点与点重合.
 (1)、操作探究1:小凡将图1中的两个全等的和按图2方式摆放,点落在上,所在直线交所在直线于点 , 连结 , 求证: .(2)、操作探究2:小彬将图1中的绕点按逆时针方向旋转角度 , 然后,分别延长、 , 它们相交于点 . 如图3,在操作中,小彬提出如下问题,请你解答:
(1)、操作探究1:小凡将图1中的两个全等的和按图2方式摆放,点落在上,所在直线交所在直线于点 , 连结 , 求证: .(2)、操作探究2:小彬将图1中的绕点按逆时针方向旋转角度 , 然后,分别延长、 , 它们相交于点 . 如图3,在操作中,小彬提出如下问题,请你解答:①时,求证:为等边三角形;
②当 时, . (直接回答即可)
(3)、操作探究3:小颖将图1中的绕点A按顺时针方向旋转角度 , 线段和相交于点 , 当旋转到点是边的中点时(可利用图4画图),直接写出线段的长为 .19. 如图,在平面直角坐标系中,直线与x轴,y轴交于B、A两点. (1)、求A、B两点的坐标;(2)、将线段AB向左平移2个单位,再向下平移4个单位得到线段CD,如图所示
(1)、求A、B两点的坐标;(2)、将线段AB向左平移2个单位,再向下平移4个单位得到线段CD,如图所示①点C的坐标为 ▲ , 并求出线段CD所在直线的解析式;
②连接AC、BC,若直线AC的解析式为 , 直线BC的解析式为 , 直接写出关于x的不等式组的解集.
20. 如图1.在平面直角坐标系中,直线与轴,轴交于、两点.将直线竖直向上平移2个单位后与交于点 , 与轴交于 . (1)、求点C的坐标;(2)、连接 , 在直线上是否存在点E,使得 . 若存在,求出点的坐标;若不存在,请说明理由;(3)、如图2,已知 , , 过B作轴且;若点G沿方向以每秒2个单位长度运动,同时,点沿方向以每秒1个单位长度运动经过t秒的运动,到达处,到达处,连接、 . 问:能否平分?若能,请直接写出t的值;若不能,请说明理由.21. 如图,在平面直角坐标系中,直线交x轴于点A,交y轴于点B,一次函数:的图象交x轴于点C,交y轴于点D,与直线交于点P.
(1)、求点C的坐标;(2)、连接 , 在直线上是否存在点E,使得 . 若存在,求出点的坐标;若不存在,请说明理由;(3)、如图2,已知 , , 过B作轴且;若点G沿方向以每秒2个单位长度运动,同时,点沿方向以每秒1个单位长度运动经过t秒的运动,到达处,到达处,连接、 . 问:能否平分?若能,请直接写出t的值;若不能,请说明理由.21. 如图,在平面直角坐标系中,直线交x轴于点A,交y轴于点B,一次函数:的图象交x轴于点C,交y轴于点D,与直线交于点P.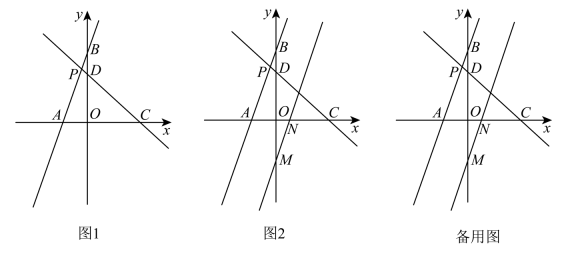 (1)、用m,n表示点P的坐标,并求的度数;(2)、若四边形的面积是 , 且 , 试求点P的坐标及直线的关系式;(3)、如图2,在(2)的条件下,将直线向下平移9个单位得到直线l,直线l交y轴于点M,交x轴于点N,若点E为射线上一动点,连接 , 在坐标轴上是否存在点F,使是以为底边的等腰直角三角形,直角顶点为F.若存在,请求出点F的坐标;若不存在,请说明理由.
(1)、用m,n表示点P的坐标,并求的度数;(2)、若四边形的面积是 , 且 , 试求点P的坐标及直线的关系式;(3)、如图2,在(2)的条件下,将直线向下平移9个单位得到直线l,直线l交y轴于点M,交x轴于点N,若点E为射线上一动点,连接 , 在坐标轴上是否存在点F,使是以为底边的等腰直角三角形,直角顶点为F.若存在,请求出点F的坐标;若不存在,请说明理由.五、实践探究题
-
22. 在中 , 点P在平面内,连接AP并将线段AP绕点A顺时针方向旋转与相等的角度,得到线段AQ , 连接BQ .
 (1)、【发现问题】如图27,如果点P是BC边上任意一点,则线段BQ和线段PC的数量关系是;(2)、【探究猜想】如图28,如果点P为平面内任意一点,前面发现的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由,请仅以图2所示的位置关系加以证明(或说明);(3)、[拓展应用]如图3,在中, , , , P是线段BC上的任意一点连接AP , 将线段AP绕点A顺时针方向旋转60°,得到线段AQ , 连接CQ , 请求出线段CQ长度的最小值.23. 如图
(1)、【发现问题】如图27,如果点P是BC边上任意一点,则线段BQ和线段PC的数量关系是;(2)、【探究猜想】如图28,如果点P为平面内任意一点,前面发现的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由,请仅以图2所示的位置关系加以证明(或说明);(3)、[拓展应用]如图3,在中, , , , P是线段BC上的任意一点连接AP , 将线段AP绕点A顺时针方向旋转60°,得到线段AQ , 连接CQ , 请求出线段CQ长度的最小值.23. 如图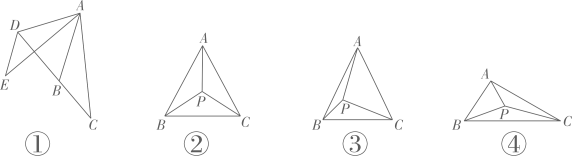 (1)、【操作发现】如图①,将△ABC绕点A顺时针旋转60°,得到△ADE,连接BD,则∠ABD=度;(2)、【类比探究】如图②,在等边三角形ABC内任取一点P,连接PA,PB,PC,求证:以PA,PB,PC的长为三边必能组成三角形;(3)、【解决问题】如图③,在边长为的等边三角形ABC内有点P,∠APC=90°,∠BPC=120°,求△APC的面积;(4)、【拓展应用】如图④是A,B,C三个村子位置的平面图,经测量,AC=4,BC=5,∠ACB=30°,P为△ABC内的一个动点,连接PA,PB,PC,求PA+PB+PC的最小值.24. 【问题背景】17世纪有着“业余数学家之王”美誉的法国律师皮耶·德·费马,提出一个问题:求作三角形内的一个点,使它到三角形三个顶点的距离之和最小后来这点被称之为“费马点”.
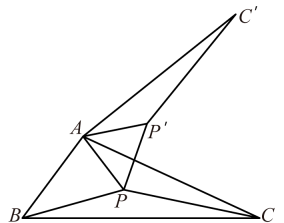
(1)、【操作发现】如图①,将△ABC绕点A顺时针旋转60°,得到△ADE,连接BD,则∠ABD=度;(2)、【类比探究】如图②,在等边三角形ABC内任取一点P,连接PA,PB,PC,求证:以PA,PB,PC的长为三边必能组成三角形;(3)、【解决问题】如图③,在边长为的等边三角形ABC内有点P,∠APC=90°,∠BPC=120°,求△APC的面积;(4)、【拓展应用】如图④是A,B,C三个村子位置的平面图,经测量,AC=4,BC=5,∠ACB=30°,P为△ABC内的一个动点,连接PA,PB,PC,求PA+PB+PC的最小值.24. 【问题背景】17世纪有着“业余数学家之王”美誉的法国律师皮耶·德·费马,提出一个问题:求作三角形内的一个点,使它到三角形三个顶点的距离之和最小后来这点被称之为“费马点”.如图,点是内的一点,将绕点逆时针旋转60°到 , 则可以构造出等边 , 得 , , 所以的值转化为的值,当 , , , 四点共线时,线段的长为所求的最小值,即点为的“费马点”.
 (1)、【拓展应用】
(1)、【拓展应用】如图1,点是等边内的一点,连接 , , , 将绕点逆时针旋转60°得到.
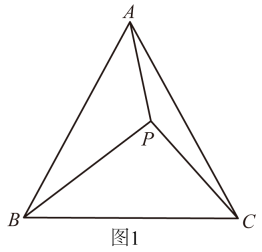
①若 , 则点与点之间的距离是 ▲ ;
②当 , , 时,求的大小;
(2)、如图2,点是内的一点,且 , , , 求的最小值.