2024年北师大版数学八(下)微素养核心突破3 垂直平分线与角平分线的性质与应用
试卷更新日期:2024-04-14 类型:复习试卷
一、选择题
-
1. 如图,已知BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,DE=5,则DF的长度是( )
 A、3 B、4 C、5 D、62. 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
A、3 B、4 C、5 D、62. 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( ) A、2 B、 C、 D、3. 如图,在四边形中, , , . 分别以点A,C为圆心,大于长为半径作弧,两弧交于点E,作射线交于点F,交于点O.若点O是的中点,则的长为( )
A、2 B、 C、 D、3. 如图,在四边形中, , , . 分别以点A,C为圆心,大于长为半径作弧,两弧交于点E,作射线交于点F,交于点O.若点O是的中点,则的长为( ) A、1 B、2 C、3 D、44. 如图,在中,已知 , , 的周长为 , 分别以A、B两点为圆心,大于的长为半径画弧,两弧相交于点M , N , 连接与相交于点D , 则的周长为( )
A、1 B、2 C、3 D、44. 如图,在中,已知 , , 的周长为 , 分别以A、B两点为圆心,大于的长为半径画弧,两弧相交于点M , N , 连接与相交于点D , 则的周长为( )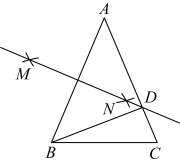 A、 B、 C、 D、5. 如图,在中,平分 , 平分 , 点是、的垂直平分线的交点,连接、 , 若 , 则的大小为( )
A、 B、 C、 D、5. 如图,在中,平分 , 平分 , 点是、的垂直平分线的交点,连接、 , 若 , 则的大小为( ) A、 B、 C、 D、6. 如图,在中,直线是线段的垂直平分线,若 , 的周长为13,则的周长为( )
A、 B、 C、 D、6. 如图,在中,直线是线段的垂直平分线,若 , 的周长为13,则的周长为( )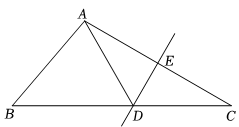 A、26 B、16 C、19 D、227. 如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC、AD于点E、F,若BE=3,AF=5,则矩形ABCD的周长为( )
A、26 B、16 C、19 D、227. 如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC、AD于点E、F,若BE=3,AF=5,则矩形ABCD的周长为( )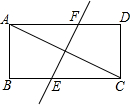 A、24 B、16 C、12 D、88. 如图,在矩形ABCD中,对角线AC与BD交于点O,∠BAD的平分线交BC于E,若 , 则∠COE=( )
A、24 B、16 C、12 D、88. 如图,在矩形ABCD中,对角线AC与BD交于点O,∠BAD的平分线交BC于E,若 , 则∠COE=( ) A、45 B、60 C、75 D、309. 如图,在 中, , , 是 的平分线, 于点 ,若 的周长等于12,则 的长是( )
A、45 B、60 C、75 D、309. 如图,在 中, , , 是 的平分线, 于点 ,若 的周长等于12,则 的长是( )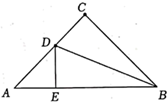 A、6 B、10 C、12 D、2410. 直线 与表示三条相互交叉的公路,现要三条公路的内部建个货物中转站,要求它到三条公路的距离相等,那么选择油库的位置有( )处
A、6 B、10 C、12 D、2410. 直线 与表示三条相互交叉的公路,现要三条公路的内部建个货物中转站,要求它到三条公路的距离相等,那么选择油库的位置有( )处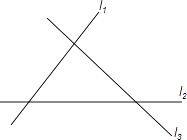 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,矩形纸片中, , E为上一点,平分 , , 则的长为 .
 12. 如图,点O为直线上一点,过点O作射线 , 使 , 将一块透明的三角尺直角顶点放在点O处,并绕点O旋转一周,在旋转过程中,当直线恰好平分锐角时, .
12. 如图,点O为直线上一点,过点O作射线 , 使 , 将一块透明的三角尺直角顶点放在点O处,并绕点O旋转一周,在旋转过程中,当直线恰好平分锐角时, . 13. 如图,在锐角中, , , 的平分线AD交BC于点D,点M,N分别是线段AD和AB上的两个动点,则的最小值是 .
13. 如图,在锐角中, , , 的平分线AD交BC于点D,点M,N分别是线段AD和AB上的两个动点,则的最小值是 . 14. 如图,中, , , 的外角平分线与边的垂直平分线交于点D,则 .
14. 如图,中, , , 的外角平分线与边的垂直平分线交于点D,则 . 15. 如图,在△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=4,CF=1,则AC的长为 .
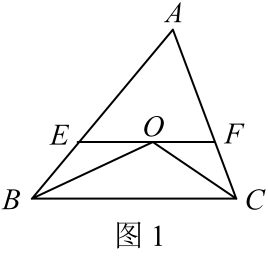
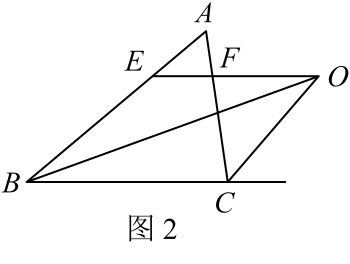
15. 如图,在△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=4,CF=1,则AC的长为 . 16. 已知如图等腰△ABC , AB=AC , ∠BAC=120°,AD⊥BC于点D , 点N是BA延长线上一点,点M是线段AD上一点,MN=MC , 下列结论中正确的结论序号是 .
16. 已知如图等腰△ABC , AB=AC , ∠BAC=120°,AD⊥BC于点D , 点N是BA延长线上一点,点M是线段AD上一点,MN=MC , 下列结论中正确的结论序号是 .①∠ACM=∠ANM;②∠ANM+∠NCB=90°;③NC=NM;④AM+AN=AB .

三、作图题
-
17. 如图,两公路与相交于点O,两公路内侧有两工厂C和D,现要修建一货站使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹)
 18. 请用直尺、圆规作图,不写作法,但要保留作图痕迹.
18. 请用直尺、圆规作图,不写作法,但要保留作图痕迹.已知:如图,四边形ABCD.
求作:点P,使点P在四边形ABCD内部,PB=PC,并且点P到∠BAD两边的距离相等.

四、解答题
-
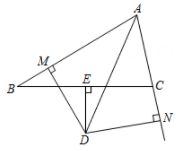
19. 已知在中,∠CAB的平分线AD与BC的垂直平分线DE交于点D, DM丄AB与M, DN丄AC交AC的延长线于N,你认为BM与CN之间有什么关系?试证明你的发现.
 20. 用三角尺可以画角平分线:如图所示,在已知的两边上分别取点M,N,使 , 再过点M画的垂线,过点N画的垂线,两垂线交于点P,那么射线就是的平分线.请你证明这一结论.
20. 用三角尺可以画角平分线:如图所示,在已知的两边上分别取点M,N,使 , 再过点M画的垂线,过点N画的垂线,两垂线交于点P,那么射线就是的平分线.请你证明这一结论.
五、综合题
-
21. 如图,在中,是边上一点,垂直平分 , .
 (1)、求证:为等腰三角形.(2)、若 , 则线段 , , 满足什么数量关系?并说明理由,22. 如图,OF是∠MON的平分线,点A在射线OM上,P,Q是直线ON上的两动点,点Q在点P的右侧,且PQ=OA,作线段OQ的垂直平分线,分别交直线OF,ON于点B,点C,连接AB,PB.
(1)、求证:为等腰三角形.(2)、若 , 则线段 , , 满足什么数量关系?并说明理由,22. 如图,OF是∠MON的平分线,点A在射线OM上,P,Q是直线ON上的两动点,点Q在点P的右侧,且PQ=OA,作线段OQ的垂直平分线,分别交直线OF,ON于点B,点C,连接AB,PB. (1)、如图1,当P,Q两点都在射线ON上时,则线段AB与PB的数量关系是;(2)、如图2,当P,Q两点都在射线ON的反向延长线上时线段AB,PB是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由.23. 数学课上,老师提出了如下问题:
(1)、如图1,当P,Q两点都在射线ON上时,则线段AB与PB的数量关系是;(2)、如图2,当P,Q两点都在射线ON的反向延长线上时线段AB,PB是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由.23. 数学课上,老师提出了如下问题:尺规作图:作△ABC中BC边上的高线.
已知:△ABC.
求作:△ABC中BC边上的高线AD.

下面是小东设计的“作△ABC中BC边上的高线”的尺规作图过程.
作法:如图,
①以点B为圆心,以BA长为半径作弧,以点C为圆心,以CA长为半径作弧,两弧在BC下方交于点E;
②连接AE交BC于点D.
所以线段AD是△ABC中BC边上的高线.
根据小东设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形.(保留作图痕迹)(2)、小乐和小马帮助小东完成下面的证明.小乐证明:
∵ , ,
∴点B,C分别在线段AE的垂直平分线上(依据1)
∴BC垂直平分线段AE.
∴线段AD是△ABC中BC边上的高线.
小马证明:
∵ , , ,
∴△ABC≌△EBC
∴
又∵
∴(依据2)
线段AD是△ABC中BC边上的高.
上述证明过程中的“依据1”和“依据2”分别是什么?
(3)、请你用不同于小东作图的方法完成老师提出的问题.(尺规作图,不写作法,只保留作图痕迹) (4)、若 , , , 则BC边上的高AD的长度为 .
(4)、若 , , , 则BC边上的高AD的长度为 .