2024年北师大版数学八(下)微素养核心突破2 等边三角形的探索类问题
试卷更新日期:2024-04-14 类型:复习试卷
一、选择题
-
1. 如图,是等边三角形,D是线段上一点(不与点B,C重合),连接 , 点E,F分别在线段 , 的延长线上,且 , 点D从B运动到C的过程中,周长的变化规律是( )
 A、先变小后变大 B、先变大后变小 C、一直变小 D、不变2. 如图所示,边长为2的等边三角形ABC中,D点在边BC上运动(不与B、C重合),点E在边AB的延长线上,点F在边AC的延长线上,AD=DE=DF.点D在BC边上从B至C的运动过程中,△BED周长变化规律为( )
A、先变小后变大 B、先变大后变小 C、一直变小 D、不变2. 如图所示,边长为2的等边三角形ABC中,D点在边BC上运动(不与B、C重合),点E在边AB的延长线上,点F在边AC的延长线上,AD=DE=DF.点D在BC边上从B至C的运动过程中,△BED周长变化规律为( )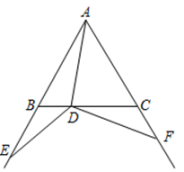 A、不变 B、一直变小 C、先变大后变小 D、先变小后变大3. 如图,在平面直角坐标系中, , , , …都是等边三角形,其边长依次为2,4,6,…,其中点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 , …,按此规律排下去,则点的坐标为( )
A、不变 B、一直变小 C、先变大后变小 D、先变小后变大3. 如图,在平面直角坐标系中, , , , …都是等边三角形,其边长依次为2,4,6,…,其中点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 , …,按此规律排下去,则点的坐标为( )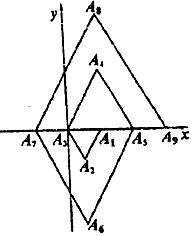 A、 B、 C、 D、4. 如图, , 在上截取 . 过点作 , 交于点 , 以点为圆心,为半径画弧,交于点;过点作 , 交于点 , 以点为圆心,为半径画弧,交于点;按此规律,所得线段的长等于( )
A、 B、 C、 D、4. 如图, , 在上截取 . 过点作 , 交于点 , 以点为圆心,为半径画弧,交于点;过点作 , 交于点 , 以点为圆心,为半径画弧,交于点;按此规律,所得线段的长等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
5. 数学课上,李老师出示了如下的题目:
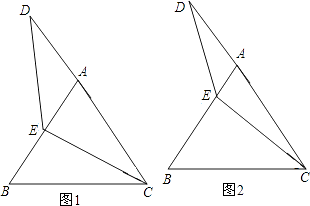
“在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图,试确定线段AE与DB的大小关系,并说明理由”.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
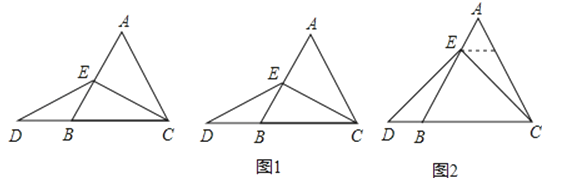
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AEDB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).理由如下:如图2,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,CD= (请你直接写出结果).
 6. 如图,是边长为1的等边三角形,分别取边的中点D、E,连接 , 作得到四边形 , 它的周长记作;分别取的中点 , 连接 , 作 , 得到四边形 , 它的周长记作 , …,照此规律作下去,则等于 .
6. 如图,是边长为1的等边三角形,分别取边的中点D、E,连接 , 作得到四边形 , 它的周长记作;分别取的中点 , 连接 , 作 , 得到四边形 , 它的周长记作 , …,照此规律作下去,则等于 .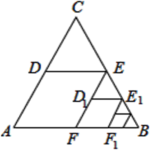 7. 如图,∠MON=30°,点B1在边OM上,且OB1=2,过点B1作B1A1⊥OM交ON于点A1 , 以A1B1为边在A1B1右侧作等边三角形A1B1C1;过点C1作OM的垂线分别交OM、ON于点B2、A2 , 以A2B2为边在A2B2的右侧作等边三角形A2B2C2;过点C2作OM的垂线分别交OM、ON于点B3、A3 , 以A3B3为边在A3B3的右侧作等边三角形A3B3C3 , …;按此规律进行下去,则△AnBn+1Cn的面积为 . (用含正整数n的代数式表示)
7. 如图,∠MON=30°,点B1在边OM上,且OB1=2,过点B1作B1A1⊥OM交ON于点A1 , 以A1B1为边在A1B1右侧作等边三角形A1B1C1;过点C1作OM的垂线分别交OM、ON于点B2、A2 , 以A2B2为边在A2B2的右侧作等边三角形A2B2C2;过点C2作OM的垂线分别交OM、ON于点B3、A3 , 以A3B3为边在A3B3的右侧作等边三角形A3B3C3 , …;按此规律进行下去,则△AnBn+1Cn的面积为 . (用含正整数n的代数式表示)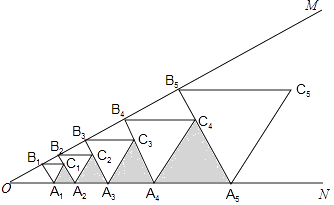 8. 在平面直角坐标系中,将若干个边长为1个单位长度的等边三角形,按如图中的规律摆放.点P从原点O出发,以每秒1个单位长度的速度沿着等边三角形的边“OA1→A1A2→A2A3→A3A4→A4A5…”的路线运动,设第n秒运动到点Pn(n为正整数),则点P18的坐标是.
8. 在平面直角坐标系中,将若干个边长为1个单位长度的等边三角形,按如图中的规律摆放.点P从原点O出发,以每秒1个单位长度的速度沿着等边三角形的边“OA1→A1A2→A2A3→A3A4→A4A5…”的路线运动,设第n秒运动到点Pn(n为正整数),则点P18的坐标是. 9. 如图,在平面直角坐标系中,△AA1C1是边长为1的等边三角形,点C1在y轴的正半轴上,以AA2=2为边长画等边△AA2C2;以AA3=4为边长画等边△AA3C3 , …,按此规律继续画等边三角形,则点An的坐标为 .
9. 如图,在平面直角坐标系中,△AA1C1是边长为1的等边三角形,点C1在y轴的正半轴上,以AA2=2为边长画等边△AA2C2;以AA3=4为边长画等边△AA3C3 , …,按此规律继续画等边三角形,则点An的坐标为 .
三、解答题
-
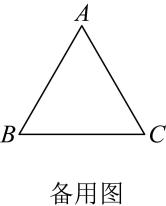
10. 等边△ABC中,点E在AB上,点D在CA的延长线上,且ED=EC.试探索以下问题:
 (1)、如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:(2)、如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。11. 综合与实践
(1)、如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:(2)、如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。11. 综合与实践特例感知:
如图1,在等边三角形中,是延长线上一点,且 , 以为边作等边三角形 , 连接 , 分别过点作 , 过点作 , 交于点 , 连接与交于点 .


 (1)、试判断和的数量关系,并说明理由.(2)、猜想论证:将绕点按顺时针方向旋转一定角度得到图2,则(1)中和的数量关系是否仍然成立?请说明理由.(3)、拓展延伸:将如图1所示的绕点按逆时针方向旋转角度 , 当时,请直接写出的值.12. 我们新定义一种三角形:两边的平方和等于第三边平方的2倍的三角形叫可爱三角形.(1)、①根据“可爱三角形”的定义,请判断:等边三角形一定(填“是”或“不是”)可爱三角形;
(1)、试判断和的数量关系,并说明理由.(2)、猜想论证:将绕点按顺时针方向旋转一定角度得到图2,则(1)中和的数量关系是否仍然成立?请说明理由.(3)、拓展延伸:将如图1所示的绕点按逆时针方向旋转角度 , 当时,请直接写出的值.12. 我们新定义一种三角形:两边的平方和等于第三边平方的2倍的三角形叫可爱三角形.(1)、①根据“可爱三角形”的定义,请判断:等边三角形一定(填“是”或“不是”)可爱三角形;②若三角形的三边长分别是4, , , 则该三角形(填“是”或“不是”)可爱三角形;
(2)、若是可爱三角形, , , 求的长.13. 在学习等边三角形的过程中,小睿同学发现一个规律:在等边△ABC中,点D是AB边上任意一点,连接CD , 过点A的射线AE交BC于点E , 交CD于点F , 当∠BAE=∠ACD时,则必有BD=CE . 为验证此规律的正确性,小睿的思路是:先利用图,作∠BAE=∠ACD , 再通过证全等得出结论.请根据小睿的思路完成以下作图与填空: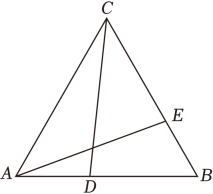 (1)、用直尺和圆规在图的基础上作∠BAE=∠ACD , AE交BC于点E , 交CD于点F . (不写作法,不下结论,只保留作图痕迹)(2)、证明:∵△ABC为等边三角形
(1)、用直尺和圆规在图的基础上作∠BAE=∠ACD , AE交BC于点E , 交CD于点F . (不写作法,不下结论,只保留作图痕迹)(2)、证明:∵△ABC为等边三角形∴AC=AB=BC , ( ) ①
在△ACD和△BAE中
∴△ACD≌△BAE(ASA)
∴ ▲ ③
又∵AB=BC
∴AB﹣AD= ▲ ④
∴BD=CE .
14. 综合与探究如图,在△ABC中,以AB , BC为边分别作等边△ABD和等边△BCE , 连接AE和DC .
 (1)、如图1,写出AE和DC之间的数量关系,并证明.(2)、如图2,若DC与AE相交于点M , 求证:∠CME=60°.(3)、如图3,取AE , DC的中点Q , P , 连接BP , PQ , BQ , 得到△BPQ , 试猜想△BPQ的形状,并证明你的猜想.15. 探究题:如图:
(1)、如图1,写出AE和DC之间的数量关系,并证明.(2)、如图2,若DC与AE相交于点M , 求证:∠CME=60°.(3)、如图3,取AE , DC的中点Q , P , 连接BP , PQ , BQ , 得到△BPQ , 试猜想△BPQ的形状,并证明你的猜想.15. 探究题:如图: (1)、△ABC为等边三角形,动点D在边CA上,动点P在边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立吗?请证明你的结论;(2)、如果把原题中“动点D在边CA上,动点P边BC上,”改为“动点D,P在射线CA和射线BC上运动”,其他条
(1)、△ABC为等边三角形,动点D在边CA上,动点P在边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立吗?请证明你的结论;(2)、如果把原题中“动点D在边CA上,动点P边BC上,”改为“动点D,P在射线CA和射线BC上运动”,其他条件不变,如图(2)所示,两点运动过程中∠BQP的大小保持不变.请你利用图(2)的情形,
求证:∠BQP=60°;
(3)、如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动,连接PD交BC于E”,其他条件不变,如图(3),则动点D,P在运动过程中,DE始终等于PE吗?写出证明过程.16. 数学是一门充满乐趣、奥妙、又极具探索的学科,对一个人的思维也是一种“挑战”.几何图形更是变幻无穷,但只要我们借助图形的直观、特殊情形出发,逐步“从特殊到一般”进行探索,思路和方法自然就会显现出来.下面是一道探索几何图形中线段AE与DB数量关系的例子:已知,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.小强的思路是: (1)、(特例探索)如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:AEDB(选填“>”、“<”或“=”).(2)、(特例引路)如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论并加以理由说明,格式如:答:AE ▲ DB(选填“>”、“<”或“=”);理由如下,过点E作EF∥BC交AC于点F.(请你将接下来的解答过程补充完整).(3)、(拓展延伸)在等边三角形ABC中,当点E在直线AB上(在线段AB外),点D在线段CB的延长线上时,同样ED=EC,若已知△ABC的边长为1,AE=2,则请你帮助小强求出CD的长.(请你画出相应图形,并简要写出求CD长的过程).17. 探索研究:已知:△ABC和△CDE都是等边三角形.
(1)、(特例探索)如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:AEDB(选填“>”、“<”或“=”).(2)、(特例引路)如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论并加以理由说明,格式如:答:AE ▲ DB(选填“>”、“<”或“=”);理由如下,过点E作EF∥BC交AC于点F.(请你将接下来的解答过程补充完整).(3)、(拓展延伸)在等边三角形ABC中,当点E在直线AB上(在线段AB外),点D在线段CB的延长线上时,同样ED=EC,若已知△ABC的边长为1,AE=2,则请你帮助小强求出CD的长.(请你画出相应图形,并简要写出求CD长的过程).17. 探索研究:已知:△ABC和△CDE都是等边三角形. (1)、如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为: ,
(1)、如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为: ,线段AD与BE所成的锐角度数为°;
(2)、如图2,当点A、C、E不在一条直线上时,请证明(1)中的结论仍然成立;灵活运用:
如图3,某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,试求水池两旁B、D两点之间的距离.
18. 探究等边三角形“手拉手”问题. (1)、如图1,已如△ABC,△ADE均为等边三角形,点D在线段BC上,且不与点B、点C重合,连接CE,试判断CE与BA的位置关系,并说明理由;(2)、如图2,已知△ABC、△ADE均为等边三角形,连接CE、BD,若∠DEC=60°,试说明点B,点D,点E在同一直线上;(3)、如图3,已知点E在ABC外,并且与点B位于线段AC的异侧,连接BE、CE.若∠BEC=60°,猜测线段BE、AE、CE三者之间的数量关系,并说明理由.19. 在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系.
(1)、如图1,已如△ABC,△ADE均为等边三角形,点D在线段BC上,且不与点B、点C重合,连接CE,试判断CE与BA的位置关系,并说明理由;(2)、如图2,已知△ABC、△ADE均为等边三角形,连接CE、BD,若∠DEC=60°,试说明点B,点D,点E在同一直线上;(3)、如图3,已知点E在ABC外,并且与点B位于线段AC的异侧,连接BE、CE.若∠BEC=60°,猜测线段BE、AE、CE三者之间的数量关系,并说明理由.19. 在等边△ABC的两边AB、AC所在直线上分别有两点M、N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系. (1)、如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是;此时 ;(2)、如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想( I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)、如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.20. 在等边 的两边AB、AC所在直线上分别有两点M、N,D为 外一点,且 , ,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及 的周长Q与等边 的周长L的关系.
(1)、如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是;此时 ;(2)、如图2,点M、N在边AB、AC上,且当DM≠DN时,猜想( I)问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.(3)、如图3,当M、N分别在边AB、CA的延长线上时,探索BM、NC、MN之间的数量关系如何?并给出证明.20. 在等边 的两边AB、AC所在直线上分别有两点M、N,D为 外一点,且 , ,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系及 的周长Q与等边 的周长L的关系. (1)、如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是; 此时 ;(2)、如图2,点M、N边AB、AC上,且当DM DN时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;(3)、如图3,当M、N分别在边AB、CA的延长线上时,若AN= ,则Q=(用 、L表示).21. 综合与实践:
(1)、如图1,当点M、N边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是; 此时 ;(2)、如图2,点M、N边AB、AC上,且当DM DN时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;(3)、如图3,当M、N分别在边AB、CA的延长线上时,若AN= ,则Q=(用 、L表示).21. 综合与实践:问题情境:
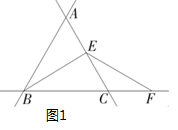
在数学综合与实践课上,张老师启示大家利用直线、线段以及点的运动变换进行探究活动.变换条件如下:如图1,直线AB,AC,BC两两相交于A,B,C三点,得知△ABC是等边三角形,点E是直线AC上一动点(点E不与点A,C重合),点F在直线BC上,连接BE,EF,使EF=BE.
独立思考:
(1)、张老师首先提出了这样一个问题:如图1,当E是线段AC的中点时,确定线段AE与CF的数量关系,请你直接写出结论:AECF(填“>”“<”或“=”).提出问题:
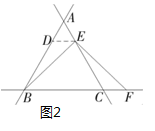
(2)、“奋斗”小组受此问题的启发,提出问题:若点E是线段AC上的任意一点,其他条件不变,(1)中的结论是否成立?该小组认为结论仍然成立,理由如下:如图2,过点E作ED∥BC,交AB于点D.(请你补充完整证明过程)(3)、“缜密”小组提出的问题是:动点E的运动位置如图3,图4所示,其他条件不变,根据题意补全图形,并判断线段AE与CF的数量关系是否发生变化?请你选择其中一种予以证明.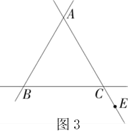
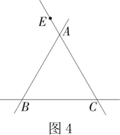 (4)、“爱心”小组提出的问题是:若等边△ABC的边长为 ,AE=1,则BF的长为.(请你直接写出结果).22. (阅读材科)小明同学发现这样一个规律:两个顶角相等的等腰三角形,
(4)、“爱心”小组提出的问题是:若等边△ABC的边长为 ,AE=1,则BF的长为.(请你直接写出结果).22. (阅读材科)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.
 (1)、(材料理解)在图1中证明小明的发现.(2)、(深入探究)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有.(将所有正确的序号填在横线上).(3)、(延伸应用)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.23. 如图1,△ABC、△DCE均为等边三角形,当B、C、E三点在同一条直线上时,连接BD、AE交于点F,易证:△ACE≌△BCD.聪明的小明将△DCE绕点C旋转的过程中发现了一些不变的结论,让我们一起开启小明的探索之旅!
(1)、(材料理解)在图1中证明小明的发现.(2)、(深入探究)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有.(将所有正确的序号填在横线上).(3)、(延伸应用)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.23. 如图1,△ABC、△DCE均为等边三角形,当B、C、E三点在同一条直线上时,连接BD、AE交于点F,易证:△ACE≌△BCD.聪明的小明将△DCE绕点C旋转的过程中发现了一些不变的结论,让我们一起开启小明的探索之旅! (1)、(探究一)如图2,当B、C、E三点不在同一条直线上时,小明发现∠BFE的大小没有发生变化,请你帮他求出∠BFE的度数.
(1)、(探究一)如图2,当B、C、E三点不在同一条直线上时,小明发现∠BFE的大小没有发生变化,请你帮他求出∠BFE的度数. (2)、(探究二)阅读材料:在平时的练习中,我们曾探究得到这样一个正确的结论:两个全等三角形的对应边上的高相等.例如:如图3,如果△ABC≌△A’B’C’,AD、A’D’分别是△ABC、△A’B’C’的边BC、B’C’上的高,那么容易证明AD=A’D’.小明带着这样的思考又有了新的发现:如图4,若连接CF,则CF平分∠BFE,请你帮他说明理由.
(2)、(探究二)阅读材料:在平时的练习中,我们曾探究得到这样一个正确的结论:两个全等三角形的对应边上的高相等.例如:如图3,如果△ABC≌△A’B’C’,AD、A’D’分别是△ABC、△A’B’C’的边BC、B’C’上的高,那么容易证明AD=A’D’.小明带着这样的思考又有了新的发现:如图4,若连接CF,则CF平分∠BFE,请你帮他说明理由.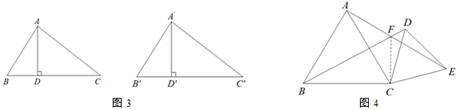 (3)、(探究三)在探究二的基础上,小明又进一步研究发现,线段AF、BF、CF之间还存在一定的数量关系,请你写出它们之间的关系,并说明理由.
(3)、(探究三)在探究二的基础上,小明又进一步研究发现,线段AF、BF、CF之间还存在一定的数量关系,请你写出它们之间的关系,并说明理由.