2024年北师大版数学八（下）微素养核心突破1 等腰三角形中的分类讨论

试卷更新日期：2024-04-14 类型：复习试卷

进入出卷网下载

一、选择题

1. 已知一个等腰三角形的两边长分别为 $3$ 和 $5$ ，则它的周长为（）

A、 $11$ B、 $13$ C、 $11$ 或 $13$ D、 $12$ 或 $13$

查看试题解析
2. 如图，为了让电线杆垂直于地面，工程人员的操作方法通常是：从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC ，当固定点B ， C到杆脚E的距离相等，且B ， E ， C在同一直线上时，电线杆DE就垂直于BC ．工程人员这种操作方法的依据是（　　）

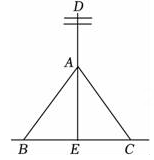A、等边对等角 B、等腰三角形“三线合一” C、垂线段最短 D、线段垂直平分线上的点到这条线段两端点的距离相等

查看试题解析
3. 如图，在 $4 \times 4$ 的正方形网格中有两个格点A、B ，连接AB ，在网格中再找一个格点C ，使得 $△ A B C$ 是等腰三角形，满足条件的格点C的个数是（）

A、5 B、6 C、8 D、9

查看试题解析
4. 已知等腰三角形的两边长分别为6和2，则这个三角形的周长是（）

A、14 B、10 C、14或10 D、12

查看试题解析
5. 如图， $A$ ， $B$ 为 $4 \times 4$ 方格纸中格点上的两点，若以 $A B$ 为边，在方格中取一点 $C$ （ $C$ 在格点上），使得 $△ A B C$ 为等腰三角形，则点 $C$ 的个数为（）

A、 $9$ B、 $8$ C、 $7$ D、 $6$

查看试题解析
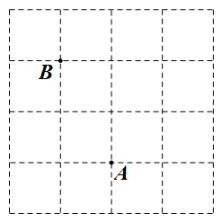6. 已知一个等腰三角形两内角的度数之比为 $1$ ： $4$ ，则这个等腰三角形的底角的度数为（）

A、 $30 °$ B、 $30 °$ 或 $120 °$ C、 $80 °$ D、 $30 °$ 或 $80 °$

查看试题解析
7. 已知等腰 $△ A B C$ ， $A B = A C$ ，若 $A B$ 边上的垂直平分线与直线 $A C$ 所夹的锐角为 $50 °$ ，则等腰 $△ A B C$ 顶角的度数为（）

A、 $65 °$ B、 $65 °$ 或 $25 °$ C、 $50 °$ D、 $40 °$ 或 $140 °$

查看试题解析
8. 如图所示，点A坐标为(-3，0) 点B坐标为(1，4)，在y轴上存在一点C，使得△ABC为等腰三角形，则满足此条件的点C最多有（）

A、4个 B、5个 C、6个 D、8个

查看试题解析

二、填空题

9. 若等腰△ABC的两条边长为6cm和2cm，则等腰三角形周长为cm．

查看试题解析
10. 如图，B是射线 $A D$ 上动点， $∠ A = 50 °$ ，若 $△ A B C$ 为等腰三角形，则 $∠ C$ 的度数可能是．

查看试题解析
11. 用一条24cm的细绳围成一个等腰三角形，若其中有一边的长为6cm，则该等腰三角形的腰长为．

查看试题解析
12. 如图，已知在Rt△ABC中， $∠ B = 90 °$ ， $A B = 3$ ， $B C = 4$ ，点D，E分别在边 $B C ， A C$ 上，连接 $A D$ ， $D E$ ，将 $△ A B D$ 沿 $A D$ 翻折，将 $△ D C E$ 沿 $D E$ 翻折，翻折后，点B，C分别落在点 $B ′$ ， $C^{'}$ 处，且边 $D B^{'}$ 与 $D C^{'}$ 在同一条直线上，连接 $A C^{'}$ ，当△ADC’是以 $A D$ 为腰的等腰三角形时，则BD= ．

查看试题解析
13. 如图，在△ABC中，AB＝AC ， ∠B＝40°，点D在线段BC上运动（D不与B、C重合），连接AD ，作∠ADE＝40°，DE交线段AC于E ，在点D的运动过程中，△ADE的形状也在改变，当△ADE是等腰三角形时，∠BDA的度数是．

查看试题解析
14. 如图， $△ A B C$ 中， $A B = A C ， ∠ B = 40 °$ ，点D是 $B C$ 上一动点，将 $△ A B D$ 沿 $A D$ 折叠得到 $△ A D E$ ，当 $△ A D E$ 与 $△ A B C$ 重叠部分是直角三角形时， $∠ B A D$ 的度数为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 140 °$ ；点D在 $B C$ 边上，将 $△ A B D$ 沿 $A D$ 所在直线翻折得 $△ A D F$ 、 $∠ F A C$ 角平分线交 $B C$ 边于点G，连接 $F G$ ， $∠ B A D = θ$ ．若 $△ D F G$ 为等腰三角形，则θ的值．

查看试题解析

三、解答题

16. 阅读材料：我们知道：若几个非负数相加得零，则这些数都必同时为零。
例如：①（a﹣1）²+（b+5）²=0，我们可以得：（a﹣1）²=0，（b+5）²=0，∴a=1，b=-5．

②若m²-4m+n²+6n+13=0，求m、n的值．

解：∵m²-4m+n²+6n+13=0，

∴（m²﹣4m+4)+(n²+6n+9)=0(我们将13拆成4和9，等式左边就出现了两个完全平方式）

∴(m﹣2)²+(n+3)²=0，

∴(m﹣2)²=0，(n+3)²=0，

∴ n=2，m=-3．

根据你的观察，探究下面的问题：

(1)、a²﹣4a+4+b²=0，则a= ． b= ．

(2)、已知x²+2xy+2y²－6y+9=0，求x^y的值．

(3)、已知a、b（a≠b）是等腰三角形的边长，且满足2a²+b²﹣8a﹣6b+17=0，求三角形的周长。

查看试题解析
17. 如图，已知：在△ABC中，AC=BC=8，∠ACB=120°，将一块足够大的直角三角尺PMN（∠M=90°，∠MPN=30°）按如图放置，顶点P在线段AB上滑动，三角尺的直角边PM始终经过点C，并且与CB的夹角∠PCB=α，斜边PN交AC于点D．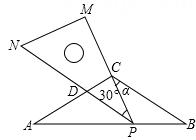

(1)、当PN∥BC时，判断△ACP的形状，并说明理由；

(2)、点P在滑动时，当AP长为多少时，△ADP与△BPC全等，并说明理由；

(3)、点P在滑动时，△PCD的形状可以是等腰三角形吗？若可以，
请直接写出夹角α的大小；若不可以，请说明理由．

查看试题解析
18. 对于平面直角坐标系 $x O y$ 中的点 $P$ 、 $Q$ ，给出如下定义：若 $P$ 、 $Q$ 为某个三角形的顶点，且边 $P Q$ 上的高 $h$ ，满足 $h = P Q$ ，则称该三角形为点 $P$ 、 $Q$ 的“等值三角形”，已知点 $A (4，0)$ ．

(1)、若点 $E (1，0)$ ，点 $F$ 在 $y$ 的正半轴上，且 $△ A E F$ 是点 $A$ 、 $E$ 的“等值三角形”，求 $F$ 的坐标；

(2)、若以线段 $O A$ 为底的等腰三角形是点 $O$ 、 $A$ 的“等值三角形”，求该三角形的腰长；

(3)、若 $R t △ A B C$ 是点 $A$ 、 $B$ 的“等值三角形”，且点 $B$ 在 $x$ 轴上，点 $C$ 在直线 $y = 2 x - 5$ 上，求点 $B$ 的坐标．

查看试题解析
19. 引入概念1：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．
引入概念2：从不等边三角形一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形．若分成的两个小三角形中一个是满足有两个角相等的三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．

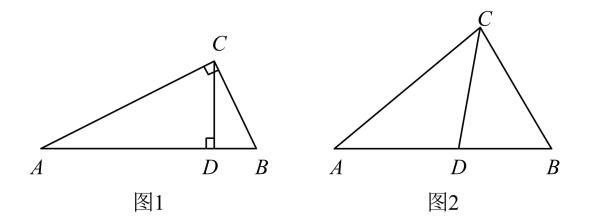(1)、【理解概念】：
如图1，在Rt△ABC中，∠ACB＝90°，CD⊥AB ，请写出图中两对“等角三角形”．
① ．；②．．

(2)、如图2，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°．请你说明CD是△ABC的等角分割线．

(3)、【应用概念】：
在△ABC中，若∠A＝40°，CD为△ABC的等角分割线，请你直接写出所有可能的∠B度数．

查看试题解析
20. 两个等腰三角形 $△ A B C$ ， $△ A D P$ ， $A B = A C$ ， $A D = A P$ ， $∠ D A P = ∠ B A C$ ，其中 $P$ 在边 $B C$ 所在的直线上 $.$ 连接 $C D$ ．

(1)、问题一：当 $∠ B A C = 90 °$ ，且点 $P$ 在线段 $B C$ 上移动时，则 $∠ B A C$ ， $∠ B C D$ 之间有怎样的数量关系？请说明理由；

(2)、问题二：当 $0 ° < ∠ B A C < 180 °$ ，且点 $P$ 还在线段 $B C$ 上移动，此时 $∠ B A C$ ， $∠ B C D$ 之间有怎样的数量关系？请说明理由；
随着探究的深入，得出一些基本的结论：当点 $P$ 在直线 $B C$ 上移动，所处的位置不同， $∠ B A C$ ， $∠ B C D$ 可能的数量关系是什么？ $($ 直接写出数量关系即可 $)$ ．

查看试题解析
21. 在“综合与探究”课上，张老师让每名同学在练习本上画出一个长方形，随后以该长方形为基本图形，以小组为单位编制一道综合探究题．经过思考和讨论，励志小组向全班同学分享了他们编拟的试题，得到了侯老师的认可，同学们也眼前一亮，纷纷动手，开始了探究．请你也跟他们一起来完成这道试题吧．如图1，分别以长方形OABC的边OC，OA所在直线为x轴、y轴，建立平面直角坐标系，已知AO＝10，AB＝6，点E在线段OC上，以直线AE为轴，把△OAE翻折，点O的对应点D恰好落在线段BC上．

(1)、分别求点D，E的坐标．

(2)、如图2，若直线AD与x轴相交于点F，求直线AD表达式及点F的坐标．

(3)、在（2）的条件下，P是x轴上的一动点，是否存在以A，P，F为顶点的三角形是等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由．

(4)、在本题的探究过程中，你感悟到哪些数学思想，请至少写出两条．

查看试题解析
22. 如图，直线l₁：y＝x＋3与过点A（3，0）的直线l₂交于点C（1，m），与x轴交于点B．

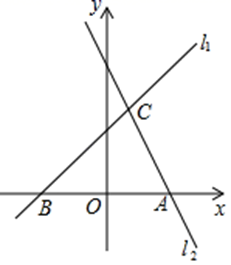(1)、求直线l₂的解析式；

(2)、点M在直线l₁上，MN∥y轴，交直线l₂于点N，若MN＝AB，求点M的坐标．

(3)、在x轴上是否存在点P，使以B、C、P为顶点的三角形是等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B = A C = 2$ ， $∠ B = 36 °$ ，点D在线段 $B C$ 上运动（点D不与点B、C重合），连接 $A D$ ，作 $∠ A D E = 36 °$ ， $D E$ 交线段 $A C$ 于点E ．

(1)、当 $∠ B D A = 128 °$ 时， $∠ E D C =$ ， $∠ A E D =$ ；

(2)、线段 $D C$ 的长度为何值时， $△ A B D ≌ △ D C E$ ？请说明理由；

(3)、在点D的运动过程中， $△ A D E$ 的形状可以是等腰三角形吗？若可以，请直接写出 $∠ B D A$ 的度数；若不可以，请说明理由．

查看试题解析