2024年浙教版数学八(下)微素养核心突破13 构造中位线
试卷更新日期:2024-04-14 类型:复习试卷
一、选择题
-
1. 老师布置的作业中有这么一道题:
如图,在中,为的中点,若 , . 则的长不可能是( )

A.5 B.7 C.8 D.9
甲同学认为AB,AC,AD这条三边不在同一个三角形中,无法解答,老师给的题目有错误。乙同学认为可以从中点出发,构造辅助线,利用全等的知识解决。丙同学认为没必要借助全等三角形的知识,只需构造一个特殊四边形,就可以解决关于三位同学的思考过程,你认为正确的是( )
A、甲 B、乙 C、丙 D、乙和丙2. 如图,在△ABC中,延长BC至点D,使得CD= BC,过AC的中点E作EF∥CD(点F位于点E右侧),且EF=2CD,连结DF.若AB=8,则DF的长为( )
 A、3 B、4 C、2 D、33. 如图,在四边形中,E、F分别是、的中点, , 若 , , 则的长度为( )
A、3 B、4 C、2 D、33. 如图,在四边形中,E、F分别是、的中点, , 若 , , 则的长度为( ) A、6 B、5 C、4 D、34. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4直线l经过点B,AE⊥l于点E,CF⊥l于点F,则AE+CF的最大值为( )
A、6 B、5 C、4 D、34. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4直线l经过点B,AE⊥l于点E,CF⊥l于点F,则AE+CF的最大值为( ) A、 B、5 C、 D、5. 如图,在 中, , , 分别是 , 的中点, , 为 上的点,连接 , .若 cm, cm, cm,则图中阴影部分面积为( )
A、 B、5 C、 D、5. 如图,在 中, , , 分别是 , 的中点, , 为 上的点,连接 , .若 cm, cm, cm,则图中阴影部分面积为( )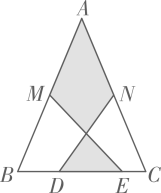 A、25cm2 B、35cm2 C、30cm2 D、42cm26. 如图,在 中, ,点 在边 上, , , .若 与 关于直线 对称,则线段 的长为( )
A、25cm2 B、35cm2 C、30cm2 D、42cm26. 如图,在 中, ,点 在边 上, , , .若 与 关于直线 对称,则线段 的长为( ) A、 B、 C、 D、7. 如图:已知 ,点 、 在线段 上且 ; 是线段 上的动点,分别以 、 为边在线段 的同侧作等边 和等边 ,连接 ,设 的中点为 ;当点 从点 运动到点 时,则点 移动路径的长是
A、 B、 C、 D、7. 如图:已知 ,点 、 在线段 上且 ; 是线段 上的动点,分别以 、 为边在线段 的同侧作等边 和等边 ,连接 ,设 的中点为 ;当点 从点 运动到点 时,则点 移动路径的长是 A、5 B、4 C、3 D、0
A、5 B、4 C、3 D、0二、填空题
-
8. 如图,在▱ABCD中,AC是对角线,∠ACD=90°,E 是BC的中点,AF平分∠BAC,连结CF,EF.若CF ⊥AF,AB=5,BC=13,则EF的长为
 9. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在直线AC上,AD=1,过点D作DE∥AB交直线BC于点E,连接'BD,点O是线段BD的中点,连接OE,则OE的长为
9. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在直线AC上,AD=1,过点D作DE∥AB交直线BC于点E,连接'BD,点O是线段BD的中点,连接OE,则OE的长为 10. 在中, , 点N是边上一点,点M为边上的动点,点D、E分别为的中点,则的最小值是 .
10. 在中, , 点N是边上一点,点M为边上的动点,点D、E分别为的中点,则的最小值是 . 11. 如图,在平行四边形中,对角线、交于点 , 将沿着对角线翻折得到 , 连接 . 若 , , , 则到的距离为 .
11. 如图,在平行四边形中,对角线、交于点 , 将沿着对角线翻折得到 , 连接 . 若 , , , 则到的距离为 . 12. 如图,▱ABCD中∠D=75°,AB=4,AC=BC,点E为线段AD上一动点,过点E作EF⊥AC于点F,连接BE,点G为BE中点,连接GF.当GF最小时,线段AF的值为 .
12. 如图,▱ABCD中∠D=75°,AB=4,AC=BC,点E为线段AD上一动点,过点E作EF⊥AC于点F,连接BE,点G为BE中点,连接GF.当GF最小时,线段AF的值为 . 13. 如图,在中,是的中点,在上且 , 连接 , 相交于点 , 则 .
13. 如图,在中,是的中点,在上且 , 连接 , 相交于点 , 则 .
三、解答题
-
14. 如图,在ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上, 且AE=CF.
 (1)、求证:四边形EGFH是平行四边形;(2)、连结BD交AC于点O,若BD= 10,AE+CF=EF ,求EG的长.15. 如图,在△ABC中,AB=AC,D,E分别为边AB,AC的中点,连结DE,BE,F,G,H分别为BE,DE,BC的中点,连结FG,FH.
(1)、求证:四边形EGFH是平行四边形;(2)、连结BD交AC于点O,若BD= 10,AE+CF=EF ,求EG的长.15. 如图,在△ABC中,AB=AC,D,E分别为边AB,AC的中点,连结DE,BE,F,G,H分别为BE,DE,BC的中点,连结FG,FH. (1)、求证:FG=FH,(2)、若∠A=90°,求证:FG⊥FH.(3)、若∠A=80°,求∠GFH的度数.16. 如图,在△ABC中,∠BAC=70°,∠ABC 和∠ACB的平分线相交于点 D,E,F,G,H 分别是线段 AB,AC,BD,CD的中点.
(1)、求证:FG=FH,(2)、若∠A=90°,求证:FG⊥FH.(3)、若∠A=80°,求∠GFH的度数.16. 如图,在△ABC中,∠BAC=70°,∠ABC 和∠ACB的平分线相交于点 D,E,F,G,H 分别是线段 AB,AC,BD,CD的中点.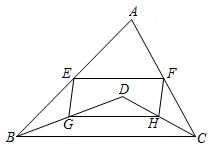 (1)、求∠BDC的度数.(2)、连结 EG,EF,HG,HF,求证:四边形EGHF 是平行四边形.17. 如图,在△ABC中,D 是边 BC 上一点,E,F,G,H分别是 BD,BC,AC,AD的中点,连结EG,HF.求证:EG,HF 互相平分.
(1)、求∠BDC的度数.(2)、连结 EG,EF,HG,HF,求证:四边形EGHF 是平行四边形.17. 如图,在△ABC中,D 是边 BC 上一点,E,F,G,H分别是 BD,BC,AC,AD的中点,连结EG,HF.求证:EG,HF 互相平分.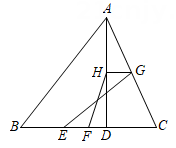 18. 如图,在矩形ABCD中,AB=6,BC=8,F为边CD的中点,E为矩形ABCD外一动点,且∠AEC=90°,求线段EF的最大值.
18. 如图,在矩形ABCD中,AB=6,BC=8,F为边CD的中点,E为矩形ABCD外一动点,且∠AEC=90°,求线段EF的最大值. 19. 下面是证明三角形中位线定理的两种添加辅助线的方法,选择其中一种,完成证明.
19. 下面是证明三角形中位线定理的两种添加辅助线的方法,选择其中一种,完成证明.三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
已知:如图,在中,点D , E分别是 , 边的中点.求证: , 且 .
 (1)、方法一:证明:如图,延长到点 , 使 , 连接 , , .
(1)、方法一:证明:如图,延长到点 , 使 , 连接 , , .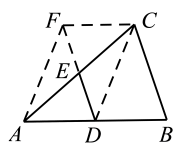 (2)、方法二:证明:如图,取中点 , 连接并延长到点 , 使 , 连接 .
(2)、方法二:证明:如图,取中点 , 连接并延长到点 , 使 , 连接 . 20. 如图 , 为等边三角形,在、上分别取点、 , 使 , 连接 .
20. 如图 , 为等边三角形,在、上分别取点、 , 使 , 连接 .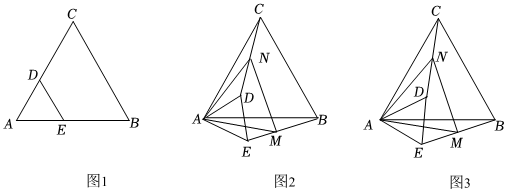 (1)、求证:是等边三角形.(2)、点、分别是、的中点,连接 , 当绕点旋转到如图的位置时,求的度数.(3)、在(2)条件下,若 , , , 求的长.
(1)、求证:是等边三角形.(2)、点、分别是、的中点,连接 , 当绕点旋转到如图的位置时,求的度数.(3)、在(2)条件下,若 , , , 求的长.四、综合题
-
21. 如图,在▱中,和的角平分线与交于点 , 且点恰好在边上.
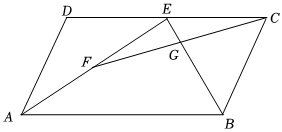 (1)、求证:为的中点;(2)、若 , , 求的长;(3)、点为的中点,连接 , 交于点 , 求证: .22. 如图,在△ABC中,点D,E分别是边AB,BC的中点,点F,G是边AC的三等分点,DF,EG的延长线相交于点H.
(1)、求证:为的中点;(2)、若 , , 求的长;(3)、点为的中点,连接 , 交于点 , 求证: .22. 如图,在△ABC中,点D,E分别是边AB,BC的中点,点F,G是边AC的三等分点,DF,EG的延长线相交于点H.
求证:
(1)、DF//BG,DF= BG;(2)、四边形FBGH是平行四边形;(3)、四边形ABCH是平行四边形.23. 已知,是的中线,过点C作 . (1)、如图1,交于点F,连接 . 求证:四边形是平行四边形;(2)、P是线段上一点(不与点A,D重合),交于点F,交于点E,连接 .
(1)、如图1,交于点F,连接 . 求证:四边形是平行四边形;(2)、P是线段上一点(不与点A,D重合),交于点F,交于点E,连接 .①如图2,四边形是平行四边形吗?请说明理由.
②如图3,延长交于点Q,若 , , ,请直接写出的值.
24. 如图,在中, , , , 分别为上两动点, . (1)、如图1,若于交于 , 求证:;(2)、如图2,若交于 , , , 求证:;(3)、如图3,若 , 将绕点顺时针旋转得 , 为中点,当取得最小值时,请直接写出的面积.25. 在平行四边形ABCD中,连接BD,若BD⊥CD,点E为边AD上一点,连接CE,交BD于点F.
(1)、如图1,若于交于 , 求证:;(2)、如图2,若交于 , , , 求证:;(3)、如图3,若 , 将绕点顺时针旋转得 , 为中点,当取得最小值时,请直接写出的面积.25. 在平行四边形ABCD中,连接BD,若BD⊥CD,点E为边AD上一点,连接CE,交BD于点F. (1)、如图1,若点E为AD中点,对角线AC与BD相交于点O,且△DFE的面积为 , DF=2,求CD的长;(2)、如图2,若点G在BD上,且DG=AB,连接CG,过G作GH⊥CE于点H,连接DH并延长交AB于点M,若 , 用等式表示线段BM,DH,BD的数量关系,并证明;(3)、如图3,若∠ABC=120°,AB=2,点N在BC边上,BC=4CN,且CE平分∠BCD,线段PQ(点P在点Q的左侧)在线段CE上运动,且 , 连接BP,NQ,请直接写出BP+PQ+QN的最小值.
(1)、如图1,若点E为AD中点,对角线AC与BD相交于点O,且△DFE的面积为 , DF=2,求CD的长;(2)、如图2,若点G在BD上,且DG=AB,连接CG,过G作GH⊥CE于点H,连接DH并延长交AB于点M,若 , 用等式表示线段BM,DH,BD的数量关系,并证明;(3)、如图3,若∠ABC=120°,AB=2,点N在BC边上,BC=4CN,且CE平分∠BCD,线段PQ(点P在点Q的左侧)在线段CE上运动,且 , 连接BP,NQ,请直接写出BP+PQ+QN的最小值.五、实践探究题
-
26.
 (1)、用数学的眼光观察
(1)、用数学的眼光观察如图①,在四边形ABCD中,AD=BC , P是对角线BD的中点,M是AB的中点,N是DC的中点.求证:∠PMN=∠PNM .
(2)、用数学的思维思考如图②,延长图①中的线段AD交MN的延长线于点E , 延长线段BC交MN的延长线于点F . 求证:∠AEM=∠F .
(3)、用数学的语言表达如图③,在△ABC中,AC<AB , 点D在AC上,AD=BC , M是AB的中点,N是DC的中点,连接MN并延长,与BC的延长线交于点G , 连接GD . 若∠ANM=60°,试判断△CGD的形状,并进行证明.
27. 探究题(1)、【证法回顾】证明:三角形中位线定理.
已知:如图1,DE是△ABC的中位线.
求证:DE∥BC,DE= BC.
证明:添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;请继续完成证明过程:
 (2)、【问题解决】
(2)、【问题解决】如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)、【拓展研究】如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=3 ,DF=2,∠GEF=90°,求GF的长.