2024年浙教版数学八(下)微素养核心突破12 平行四边形的折叠问题
试卷更新日期:2024-04-14 类型:复习试卷
一、选择题
-
1. 如图,在中, , , 是边上一点,将沿折叠得 , 连接 , 若四边形为平行四边形,则的值是( )
 A、 B、 C、2 D、2. 在一次活动课中,对如图所示的平行四边形(AD>AB)进行折叠,第一次沿着AE折叠,点B落在点F处,接着两组同学分别尝试了两种不同的二次折叠,并给出了判断:组1:若沿着CF的中垂线折叠,则点D与点A必重合;组2:若沿着DF折叠,AD与DC所在的直线重合,且点A的对应点仍落在直线AF上,则 = ( )
A、 B、 C、2 D、2. 在一次活动课中,对如图所示的平行四边形(AD>AB)进行折叠,第一次沿着AE折叠,点B落在点F处,接着两组同学分别尝试了两种不同的二次折叠,并给出了判断:组1:若沿着CF的中垂线折叠,则点D与点A必重合;组2:若沿着DF折叠,AD与DC所在的直线重合,且点A的对应点仍落在直线AF上,则 = ( )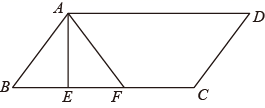 A、组1判断正确,组2判断正确 B、组1判断正确,组2判断错误 C、组1判断错误,组2判断正确 D、组1判断错误,组2判断错误3. 如图,在平行四边形ABCD中, , DF=6,E为AC上一点,将沿着DE翻折,点A恰好落在边CD上的F点处,连接BF,则BF长度为 ( ).
A、组1判断正确,组2判断正确 B、组1判断正确,组2判断错误 C、组1判断错误,组2判断正确 D、组1判断错误,组2判断错误3. 如图,在平行四边形ABCD中, , DF=6,E为AC上一点,将沿着DE翻折,点A恰好落在边CD上的F点处,连接BF,则BF长度为 ( ). A、 B、 C、 D、+24. 如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点B'处,若∠1=48°,∠2=32°,则∠B的度数为( )
A、 B、 C、 D、+24. 如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点B'处,若∠1=48°,∠2=32°,则∠B的度数为( ) A、124° B、114° C、104° D、56°5. 如图,将平行四边形ABCD沿对角线BD折叠,使点A落在E处,若∠1=56°,∠2=42°,则∠A的度数为( )
A、124° B、114° C、104° D、56°5. 如图,将平行四边形ABCD沿对角线BD折叠,使点A落在E处,若∠1=56°,∠2=42°,则∠A的度数为( )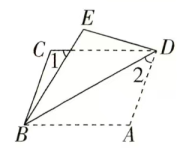 A、108° B、109° C、110° D、111°6. 如图,在平行四边形ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的大小为( )
A、108° B、109° C、110° D、111°6. 如图,在平行四边形ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的大小为( )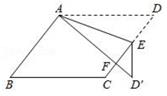 A、26° B、36° C、46° D、56°7. 如图,将平行四边形沿对边上两点连线对折,使点A恰好落在点C处,若 , , , 则的长为( ).
A、26° B、36° C、46° D、56°7. 如图,将平行四边形沿对边上两点连线对折,使点A恰好落在点C处,若 , , , 则的长为( ). A、4.6 B、 C、5.6 D、8. 如图,在平行四边形中,E为边上一点,将沿折叠至 , 与交于点F,若 , 则的大小为( )
A、4.6 B、 C、5.6 D、8. 如图,在平行四边形中,E为边上一点,将沿折叠至 , 与交于点F,若 , 则的大小为( ) A、 B、 C、 D、9. 如图,在平行四边形ABCD中,AD= , E,F分别为CD,AB上的动点,DE=BF,分别以AE,CF所在直线为对称轴翻折△ADE,△BCF,点D,B的对称点分别为G,H.若E、G、H、F恰好在同一直线上,∠GAF=45°,且GH=3,则AF的长是( )
A、 B、 C、 D、9. 如图,在平行四边形ABCD中,AD= , E,F分别为CD,AB上的动点,DE=BF,分别以AE,CF所在直线为对称轴翻折△ADE,△BCF,点D,B的对称点分别为G,H.若E、G、H、F恰好在同一直线上,∠GAF=45°,且GH=3,则AF的长是( ) A、4 B、5 C、6 D、710. 如图,在 中, ,将 折叠,使点D,C分别落在点F,E处(点F,E都在 所在的直线上),折痕为 ,则 等于( )
A、4 B、5 C、6 D、710. 如图,在 中, ,将 折叠,使点D,C分别落在点F,E处(点F,E都在 所在的直线上),折痕为 ,则 等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图将沿对角线折叠,使点落在处,若 , , 则的度数为 .
 12. 如图,将 进行折叠,折叠后 恰好经过点C得到 , , , ,则线段 的长度为 .
12. 如图,将 进行折叠,折叠后 恰好经过点C得到 , , , ,则线段 的长度为 .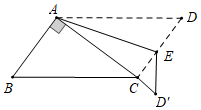 13. 如图,在平行四边形中,将沿折叠后,点恰好落在的延长线上的点处.若 , , 则的周长为 .
13. 如图,在平行四边形中,将沿折叠后,点恰好落在的延长线上的点处.若 , , 则的周长为 . 14. 如图,在平行四边形ABCD中,E为边CD上的一个点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=50°,∠DAE=20°,则∠FED′的大小为 .
14. 如图,在平行四边形ABCD中,E为边CD上的一个点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=50°,∠DAE=20°,则∠FED′的大小为 .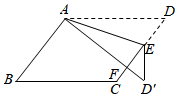 15. 如图,平行四边形中,点E在边上,以为折痕,将向上翻折,点A正好落在上的点F,若的周长为10,的周长为24,则的长为.
15. 如图,平行四边形中,点E在边上,以为折痕,将向上翻折,点A正好落在上的点F,若的周长为10,的周长为24,则的长为.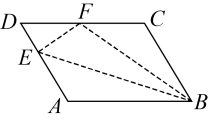 16. 如图,有一张平行四边形纸条 ABCD,AD=5cm,AB=2cm, ∠A=120°, 点E,F 分别在边 AD,BC上,DE=1cm. 现将四边形 CFED沿EF折叠,使点C,D 分别落在点C’,D '上.当点C’恰好落在边AD上时,线段 CF的长为cm .在点F 从点B 运动到点C的过程中,若边与边AD交于点M, 则点M相应运动的路径长为cm.
16. 如图,有一张平行四边形纸条 ABCD,AD=5cm,AB=2cm, ∠A=120°, 点E,F 分别在边 AD,BC上,DE=1cm. 现将四边形 CFED沿EF折叠,使点C,D 分别落在点C’,D '上.当点C’恰好落在边AD上时,线段 CF的长为cm .在点F 从点B 运动到点C的过程中,若边与边AD交于点M, 则点M相应运动的路径长为cm. 17. 数学活动课上,陈老师向同学们展示了一位同学的折纸作品(如图所示).已知平行四边形纸片 , 对角线 , 点E,F分别在边和上,交于点P.将纸片沿折叠,点A落在外的点处,B落在对角线上的点G处,交于点H,连接 . 若 , 则 .
17. 数学活动课上,陈老师向同学们展示了一位同学的折纸作品(如图所示).已知平行四边形纸片 , 对角线 , 点E,F分别在边和上,交于点P.将纸片沿折叠,点A落在外的点处,B落在对角线上的点G处,交于点H,连接 . 若 , 则 .
三、解答题
-
18. 已知:将▱ABCD纸片折叠,使得点C落在点A的位置,折痕为EF,连接CE.求证:四边形AFCE为平行四边形.
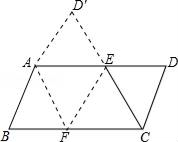 19. 已知,如图,在平行四边形ABCD中,∠B=60°,BC=6,点E为BC边的中点,△ABE沿着AE向右折叠,点B落在B'处,连接CB'并延长交AD于点F。
19. 已知,如图,在平行四边形ABCD中,∠B=60°,BC=6,点E为BC边的中点,△ABE沿着AE向右折叠,点B落在B'处,连接CB'并延长交AD于点F。 (1)、求证:四边形AECF是平行四边形;(2)、当AB'⊥CD时,求AE的长。20. 如图,把平行四边形纸片ABCD沿BD折叠,点C落在C'处,BC'与AD相交于点E.
(1)、求证:四边形AECF是平行四边形;(2)、当AB'⊥CD时,求AE的长。20. 如图,把平行四边形纸片ABCD沿BD折叠,点C落在C'处,BC'与AD相交于点E. (1)、求证:EB=ED;(2)、连结AC',求证:AC'∥BD.21. 我们知道平行四边形有很多性质.现在如果我们把平行四边形沿着它的一条对角线翻折.会发现这其中还有更多的结论,如图,已知平行四边形ABCD中,AB=2 , ∠30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D.
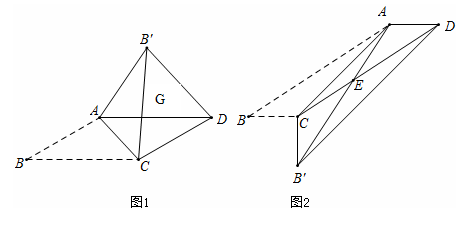
(1)、求证:EB=ED;(2)、连结AC',求证:AC'∥BD.21. 我们知道平行四边形有很多性质.现在如果我们把平行四边形沿着它的一条对角线翻折.会发现这其中还有更多的结论,如图,已知平行四边形ABCD中,AB=2 , ∠30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D.
 (1)、【发现与证明】
(1)、【发现与证明】如图1:结论①△AGC是等腰三角形;结论②B′D∥AC。请证明结论①或结论②(只需证明一个结论)。
(2)、【应用与解答】如图2:如果BC=1,AB′与CD相交于点E,求△AEC的面积。
(3)、【拓展与探索】直接写出结论,当BC的长为多少时,△AB′D是直角三角形?