2024年浙教版数学八（下）微素养核心突破11 平行四边形的动点问题

试卷更新日期：2024-04-14 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图，在平行四边形 $A B C D$ 中， $∠ C = 120 °$ ，AB=4 ，AD=8 ，点H、G分别是边CD、 $B C$ 上的动点.连接 $A H$ 、 $H G$ ，点E为 $A H$ 的中点，点 $F$ 为 $G H$ 的中点，连接 $E F$ .则 $E F$ 的最大值与最小值的差为（）

A、2 B、 $2 \sqrt{3} - 2$ C、 $\sqrt{3}$ D、 $4 - \sqrt{3}$

查看试题解析
2. 如图， ▱ABCD的顶点A，D分别在直角∠MON的两边OM，ON上运动（不与点O重合），▱ABCD的对角线AC，BD相交于点P，连接OP，若OP=5，则▱ABCD的周长最小值是（）

A、20 B、25 C、10 D、15

查看试题解析
3. 如图，平行四边形ABCD中，E，F分别是AD，BC的中点，P是边DC上的动点，G，H分别是PE，PF的中点，已知DC＝10cm，则GH的长是（）

A、7cm B、6cm C、5cm D、4cm

查看试题解析
4. 如图，在平面直角坐标系中，平行四边形ABCD的坐标分别为A（﹣1，0）、B（0，2）、C（4，2）、D（3，0），点P是AD边上的一个动点，若点A关于BP的对称点为A'，则A'C的最小值为（　　）

A、 $\sqrt{5}$ B、 $4 - \sqrt{5}$ C、 $\sqrt{5} - 1$ D、1

查看试题解析
5. 如图，在平行四边形ABCD中，∠C=120°，AD=2AB=4，点H、G分别是边CD、BC上的动点.连接AH、HG，点E为AH的中点，点F为GH的中点，连接EF，则EF的最大值与最小值的差为（）

A、1 B、 $\sqrt{3} - 1$ C、 $\frac{\sqrt{3}}{2}$ D、 $2 - \sqrt{3}$

查看试题解析
6. 如图，在Rt△ABC中，∠C=90°，AC=4，AB=8，点D是AC上一个动点，以AB为对角线的所有平行四边形ADBE中，线段DE的最小值是（）

A、4 B、 $4 \sqrt{3}$ C、 $2 \sqrt{3}$ D、6

查看试题解析
7. 将一副三角尺如图拼接：含30°角的三角尺（ $△ A B C$ ）的长直角边与含45°角的三角尺（ $△ A C D$ ）的斜边恰好重合.点E，F分别是边 $A C$ ， $B C$ 上的动点，各自同时从点A，点B向终点C运动，已知点E的速度为1单位/秒，若存在某个时刻四边形 $D E B F$ 为平行四边形，则点F的速度为（）单位/秒.

A、1 B、 $\frac{3}{4}$ C、 $\sqrt{3}$ D、2

查看试题解析
8. 在平面直角坐标系中，平行四边形ABCD的坐标分别为A（-1，0）、B（0，2）、C（3，2）、D（2，0），点P是AD边上的一个动点，若点A关于BP的对称点为 $A^{'}$ ，则 $A^{'}$ C的最小值为（）

A、 $\sqrt{5}$ B、 $3 - \sqrt{5}$ C、 $\sqrt{5} - 1$ D、1

查看试题解析

二、填空题

9. 如图，四边形ABCD 是平行四边形，点D 的纵坐标是6，CD=10，顶点A在y轴上，边 BC 在x轴上.设 P 是射线 BC上的一个动点，则当△ABP 为等腰三角形时，点P的坐标是.

查看试题解析
10. 如图，在平面直角坐标系中，O为坐标原点，四边形ABCD是平行四边形，点A，B，C的坐标分别为A(0，2)，B(-1，0)，C(4，0)，E是 BC 的中点，P 是线段AD 上的动点.若△BEP是等腰三角形，则点P 的坐标为.
·

查看试题解析
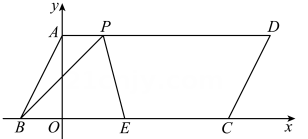11. 如图四边形ABCD，AD∥BC，AB⊥BC，AD=3，AB=6，BC=9，P为AB边上的一动点，以PD，PC为边作平行四边形PCQD，则对角线PQ的长的最小值是．

查看试题解析
12. 如图，△ABC中，AB＝AC＝10，BC＝12，D为AC边上一动点，E为平面内一点，以点B、C、D、E为顶点的四边形为平行四边形，则DE的最小值为.

查看试题解析
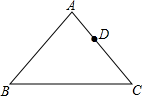13. 如图，点A，B为定点，定直线 $l$ ∥AB，P是 $l$ 上一动点，点M，N分别为PA，PB的中点，对下列各值：①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小.其中会随点P的移动而变化的是.

查看试题解析
14. 如图，矩形 $A B C D$ 中， $A B = 2 \sqrt{3}$ ， $B C = 4$ ，连结对角线 $A C$ ，E为 $A C$ 的中点，F为 $A B$ 边上的动点连结 $E F$ ，作点C关于 $E F$ 的对称点 $C^{'}$ ，连结 $C^{'} E$ ， $C^{'} F$ ，若 $△ E F C^{'}$ 与 $△ A C F$ 的重叠部分（ $△ E F G$ ）面积等于 $△ A C F$ 的 $\frac{1}{4}$ ，则 $B F =$ .

查看试题解析

三、综合题

15. 如图，在 $▱$ ABCD中，点P是对角线AC上一动点，过点P作PM∥DC，且PM=DC，连结BM，CM，BP，PD．

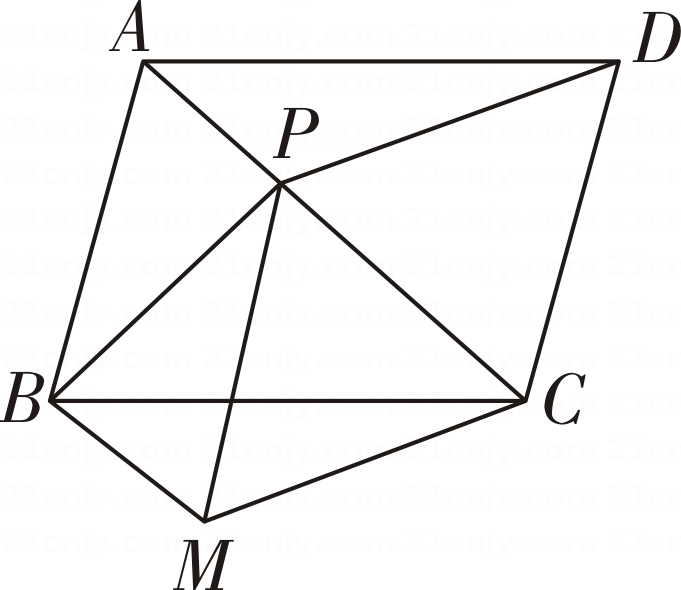(1)、求证：△ADP≌△BCM；

(2)、若PA= $\frac{1}{2}$ PC，设△ABP的面积为S，四边形BPCM的面积为T，求 $\frac{S}{T}$ 的值.

查看试题解析
16.
将一副三角尺如图拼接：含30°角的三角尺（△ABC）的长直角边与含45°角的三角尺（△ACD）的斜边恰好重合．已知AB＝2 $\sqrt{3}$ ，P是AC上的一个动点．

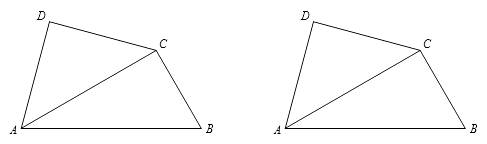(1)、当点P运动到∠ABC的平分线上时，连接DP、BP，求CP、DP的长；

(2)、当点P在运动过程中出现PD＝BC时，求此时∠PDA的度数；

(3)、当点P运动到什么位置时，以D，P，B，Q为顶点的平行四边形的顶点Q恰好在边BC上？求出此时平行四边形的面积．

查看试题解析
17. 点P是平行四边形 $A B C D$ 的对角线 $A C$ 所在直线上的一个动点（点P不与点A、C重合），分别过点A、C向直线 $B P$ 作垂线，垂足分别为点E、F.点O为 $A C$ 的中点.

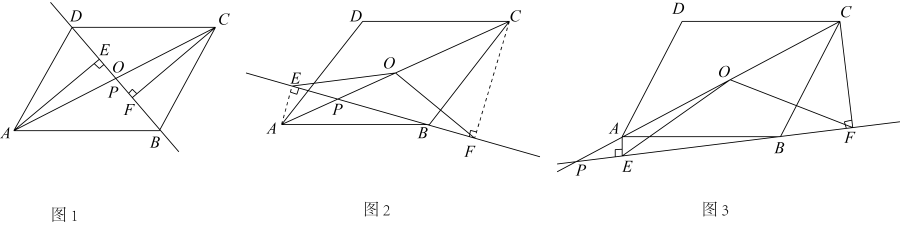(1)、如图1，当点P与点O重合时，线段 $O E$ 和 $O F$ 的关系是；

(2)、当点P运动到如图2所示的位置时，请证明（1）中的结论仍然成立.

(3)、如图3，点P在线段 $O A$ 的延长线上运动，当 $∠ O E F = 30 °$ 时，试探究线段 $C F$ 、 $A E$ 、 $O E$ 之间的关系.

查看试题解析
18. 如图1，在直角坐标系中，直线y=-2x+8交x轴于点B，交y轴于点A， C是AB的中点，动点P从点A出发沿AO方向以每秒1个单位的速度向终点O运动，同时动点Q从点O出发以每秒2个单位的速度沿射线OB方向运动．以CP，CQ为边构造 ▱ CPDQ，设点P运动的时间为t秒．

(1)、写出点C的坐标和直线OC的解析式．
点C的坐标是，直线OC的解析式是

(2)、如图2，当点Q运动到点B时，连结CD．求证： CD∥AP．

(3)、连结OC．当点D落在△AOC的边上或各边所在的直线上时，求t的值．

查看试题解析
19. 如图 $1$ ， $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 8$ ， $∠ A = 30 °$ ，动点 $P$ 从点 $B$ 出发，沿 $B A$ 方向以每秒4个单位的速度向终点 $A$ 运动，同时动点 $Q$ 从点 $C$ 出发，以每秒1个单位的速度沿 $C B$ 方向运动，当点 $P$ 到达 $A$ 点时，点 $Q$ 也停止运动，以 $B P$ ， $B Q$ 为邻边作平行四边形 $B P D Q$ ， $P D$ ， $Q D$ 分别交 $A C$ 于点 $E$ ， $F$ ，设点 $P$ 运动的时间为 $t$ 秒．

(1)、 $B Q =$ $($ 含 $t$ 的代数式表示 $)$ ；

(2)、如图2，连接 $A D$ ， $P F$ ， $P Q$ ，当 $A D ∥ P Q$ 时，求 $△ P Q F$ 的面积；

(3)、如图3，连接 $P F$ ， $P Q$ ， $D$ 点关于直线 $P F$ 的对称点为 $D^{'}$ 点，若 $D'$ 落在 $△ P Q B$ 的内部 $($ 不包括边界 $)$ 时，则 $t$ 的取值范围为.

查看试题解析
20. 如图，在平面直角坐标系中，点A，B的坐标分别是（﹣4，0），（0，8），动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从点B出发，沿射线BO方向以每秒2个单位的速度运动．以CP，CO为邻边构造▱PCOD，在线段OP延长线上取点E，使PE＝AO，设点P运动的时间为t秒．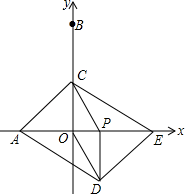

(1)、当点C运动到线段OB的中点时，求t的值及点E的坐标；

(2)、当点C在线段OB上时，求证：四边形ADEC为平行四边形；

(3)、在线段PE上取点F，使PF＝3，过点F作MN⊥PE，截取FM＝ $\sqrt{3}$ ，FN＝1，且点M，N分别在第一、四象限，在运动过程中，当点M，N中，有一点落在四边形ADEC的边上时，直接写出所有满足条件的t的值．

查看试题解析
21. 如图，在四边形ABCD中，AD∥BC，∠C＝90°，BC＝16，DC＝12，AD＝21.动点P从点D出发，沿线段DA的方向以每秒2个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点P运动到点A时，点Q随之停止运动.设运动的时间为t（秒）.

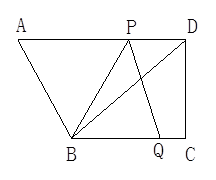(1)、当t=2时，求△BPQ的面积；

(2)、若四边形ABQP为平行四边形，求运动时间t.

(3)、当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？

查看试题解析
22. 在平面直角坐标系xOy中，A，B点的坐标分别为(0，4)，(-4，0)，P点坐标为(0，m)，点E是射线BO上的动点，满足BE=1.5OP，以PE，EO为邻边作 ▱ PEOQ．

(1)、当m=2时，求出PE的长度；

(2)、当m>0时，是否存在m的值，使得 $▱$ PEOQ的面积等于△ABO面积的 $\frac{1}{4}$ ，若存在求出m的值，若不存在，请说明理由；

(3)、当点Q在第四象限时，点Q关于E点的对称点为Q'，点Q'刚好落在直线AB上时，求m的值(直接写出答案)．

查看试题解析
23. 如图直角坐标系中直线AB与x轴正半轴、y轴正半轴交于A，B两点，已知B（0，4），∠BAO＝30°，P，Q分别是线段OB，AB上的两个动点，P从O出发以每秒3个单位长度的速度向终点B运动，Q从B出发以每秒8个单位长度的速度向终点A运动，两点同时出发，当其中一点到达终点时整个运动结束，设运动时间为t（秒）．

(1)、求线段AB的长，及点A的坐标；

(2)、t为何值时，△BPQ的面积为2 $\sqrt{3}$ ；

(3)、若C为OA的中点，连接QC，QP，以QC，QP为邻边作平行四边形PQCD，
①t为何值时，点D恰好落在坐标轴上；

②是否存在时间t使x轴恰好将平行四边形PQCD的面积分成1：3的两部分，若存在，直接写出t的值．

查看试题解析