2024年浙教版数学八（下）微素养核心突破7 配方法的应用

试卷更新日期：2024-04-14 类型：复习试卷

进入出卷网下载

一、类型1 求多项式的最值

1. 我们已经学习了利用配方法解一元二次方程，其实配方法还有其它重要应用．
例：已知x可取任何实数，试求二次三项式2x²﹣12x+14的值的范围．
解：2x²﹣12x+14=2（x²﹣6x）+14=2（x²﹣6x+3²﹣3²）+14
=2[（x﹣3）²﹣9]+14=2（x﹣3）²﹣18+14=2（x﹣3）²﹣4．
∵无论x取何实数，总有（x﹣3）²≥0，∴2（x﹣3）²﹣4≥﹣4．
即无论x取何实数，2x²﹣12x+14的值总是不小于﹣4的实数．
问题：已知x可取任何实数，则二次三项式﹣3x²+12x+11的最值情况是（）

A、有最大值﹣23 B、有最小值﹣23 C、有最大值23 D、有最小值23

查看试题解析
2. 关于多项式﹣2x²+8x+5的说法正确的是（　　）

A、有最大值13 B、有最小值﹣3 C、有最大值37 D、有最小值1

查看试题解析
3. 代数式 $x^{2} + 4 x + 5$ 的最小值是（）

A、5 B、1 C、4 D、没有最小值

查看试题解析
4. 小明和小林在探索代数式x²+ $\frac{1}{x^{2}}$ (x≠0)有没有最大（小）值时，小明做了如下探索：
∵x²+ $\frac{1}{x^{2}}$ +2-2 =(x+ $\frac{1}{x}$ )²-2≥-2，
∴小明的结论是x²+ $\frac{1}{x^{2}}$ 的最小值为-2
小林做了如下探索
∵x²+ $\frac{1}{x^{2}}$ -2+2 =(x- $\frac{1}{x}$ )²+2≥2，
小林的结论是x²+ $\frac{1}{x^{2}}$ 的最小值为2；则（）

A、小明正确 B、小林正确 C、小明和小林都正确 D、小明和小林都不正确

查看试题解析
5. 设 $a$ ， $b$ 为实数，多项式 $(x + a) (2 x + b)$ 展开后 $x$ 的一次项系数为 $p$ ，多项式 $(2 x + a) (x + b)$ 展开后 $x$ 的一次项系数为 $q$ ：若 $p + q = 6$ ，且 $p$ ， $q$ 均为正整数，则（）

A、 $a b$ 与 $\frac{a}{b}$ 的最大值相等， $a b$ 与 $\frac{a}{b}$ 的最小值也相等 B、 $a b$ 与 $\frac{a}{b}$ 的最大值相等， $a b$ 与 $\frac{a}{b}$ 的最小值不相等 C、 $a b$ 与 $\frac{a}{b}$ 的最大值不相等， $a b$ 与 $\frac{a}{b}$ 的最小值相等 D、 $a b$ 与 $\frac{a}{b}$ 的最大值不相等， $a b$ 与 $\frac{a}{b}$ 的最小值也不相等

查看试题解析
6. 不论x，y取何值，代数式 $9 x^{2} + 4 y^{2} + 6 x - 8 y + 2$ 的值（）

A、总不小于-3 B、总不大于-3 C、总大于2 D、总小于2

查看试题解析
7. 利用 $(a \pm b)^{2}$ 可求某些整式的最值．例如， $x^{2} - 2 x + 3 = (x^{2} - 2 x + 1) + 2 = (x - 1)^{2} + 2$ ，由 $(x - 1)^{2} \geq 0$ 知，当 $x = 1$ 时，多项式 $x^{2} - 2 x + 3$ 有最小值 $2$ ．对于多项式 $3 x^{2} + 2 x + 1$ ，当 $x =$ 时，有最小值是．

查看试题解析
8. 配方法不仅可以解一元二次方程，还可以求最值．
例如：求代数式 $2 x^{2} + 4 x + 5$ 的最值．
解： $2 x^{2} + 4 x + 5$
$= (2 x^{2} + 4 x) + 5$ （分离常数项）
$= 2 (x^{2} + 2 x) + 5$ （提二次项系数）
$\begin{array}{l} = 2 (x^{2} + 2 x + 1 - 1) + 5 \\ = 2 [(x + 1)^{2} - 1] + 5 \\ = 2 (x + 1)^{2} + 3 \end{array}} (配方)$
$∵ 2 (x + 1)^{2} \geq 0$
$∴ 2 (x + 1)^{2} + 3 \geq 3$
$∴$ 当 $x = - 1$ 时，代数式 $2 x^{2} + 4 x + 5$ 取得最小值是3
运用以上方法，解答下列问题：

(1)、求代数式 $- a^{2} + 6 a - 4$ 的最值；

(2)、关于 $x$ 的方程 $m x^{2} - 3 (m + 2) x + 2 m + 7 = 0 (m \neq 0)$ ．求证：无论 $m$ 取何值，方程总有两个不相等的实数根．

查看试题解析
9. [阅读材料]：把代数式通过配凑等手段，得到局部完全平方式，再进行有关运算和解题，这种解题方法叫做配方法．配方法在因式分解、解方程、求最值问题等中都有着广泛的应用．
例1：用配方法因式分解： $a^{2} + 4 a + 3$ ．
原式 $= a^{2} + 4 a + 4 - 1 = {(a + 2)}^{2} - 1 = (a + 2 - 1) (a + 2 + 1) = (a + 1) (a + 3)$
例2：求 $x^{2} + 8 x + 21$ 的最小值．
解： $x^{2} + 8 x + 21 = x^{2} + 8 x + 16 + 5 = {(x + 4)}^{2} + 5$ ；
由于 ${(x + 4)}^{2} \geq 0$ ，所以 ${(x + 4)}^{2} + 5 \geq 5$ ，
即 $x^{2} + 8 x + 21$ 的最小值为5．

(1)、[类比应用]：在横线上添上一个常数项使之成为完全平方式： $a^{2} + 6 a +$ ；

(2)、仿照例1的步骤，用配方法因式分解： $m^{2} - 10 m + 24$ ；

(3)、仿照例2的步骤，求 $4 x^{2} + 12 x + 15$ 的最小值；

(4)、若 $x^{2} + 2 y^{2} + 2 x y - 6 y + 9 = 0$ ，则 $x - y =$ ．

查看试题解析
10. 阅读材料：形如 $a^{2} \pm 2 a b + b^{2}$ 的式子叫做完全平方式，有些多项式虽然不是完全平方式，但可以通过配凑等手段，得到局部完全平方式，再进行有关运算和解题，这种解题方法叫做配方法．配方法在因式分解、代数最值等问题中都有广泛的应用．
（一）用配方法因式分解： $a^{2} + 6 a + 8$ ．

解：原式 $= a^{2} + 6 a + 9 - 1$

      $= (a + 3)^{2} - 1$

      $= (a + 3 - 1) (a + 3 + 1)$

      $= (a + 2) (a + 4)$

（二）用配方法求代数式 $a^{2} + 6 a + 8$ 的最小值．

解：原式 $= a^{2} + 6 a + 9 - 1$

      $= (a + 3)^{2} - 1$

∵ $(a + 3)^{2} \geq 0$ ， ∴ $(a + 3)^{2} - 1 \geq - 1$ ， ∴ $a^{2} + 6 a + 8$ 的最小值为 $- 1$ ．

(1)、若代数式 $x^{2} - 10 x + k$ 是完全平方式，则常数k的值为；

(2)、因式分解： $a^{2} - 12 a + 32 =$ ；

(3)、用配方法求代数式 $4 x^{2} + 4 x + 5$ 的最小值；

(4)、拓展应用：
若实数a，b满足 $a^{2} - 5 a - b + 7 = 0$ ，则 $a + b$ 的最小值为．

查看试题解析
11. 【阅读理解，自主探究】把代数式通过配凑等手段，得到完全平方式，再运用完全平方式是非负数这一性质增加问题的条件，这种解题方法叫做配方法，配方法在代数式求值，解方程，最值问题等都有着广泛的应用．
例1 用配方法因式分解：a²＋6a＋8．
原式＝ a²＋6a＋9－1＝（a＋3）²－1＝（a＋3－1）（a＋3＋1）＝（a＋2）（a＋4）．
例2若M＝a²－2ab＋2b²－2b＋2，利用配方法求M的最小值；
a²－2ab＋2b²－2b＋2＝a²－2ab＋b²＋b²－2b＋1＋1＝（a－b）²＋（b－1）²＋1；
∵（a－b）²≥0，（b－1）²≥0，
∴当a＝b＝1时，M有最小值1．
请根据上述自主学习材料解决下列问题：

(1)、在横线上添上一个常数项使之成为完全平方式：a²＋10a＋；

(2)、用配方法因式分解：a²－12a＋35．

(3)、若M＝a²－3a+1，则M的最小值为；

(4)、已知a²＋2b²＋c²－2ab＋4b－6c＋13＝0，则a＋b＋c的值为；

查看试题解析

二、类型2 比较大小

12. 已知多项式 $P = \frac{1}{2} x - 2$ ， $Q = x^{2} - \frac{3}{2} x$ （ $x$ 为任意实数），试比较多项式 $P$ 与 $Q$ 的大小．（）

A、无法确定 B、 $P > Q$ C、 $P = Q$ D、 $P < Q$

查看试题解析
13. 比较 $- \frac{1}{2} x_{}^{2} + 2 x$ 与 $- x + 5$ 的大小.

(1)、尝试(用“<”， “=”或“>”填空)：
①当x=1 时， $- \frac{1}{2} x_{}^{2} + 2 x$ $- x + 5$
②当x=0 时， $- \frac{1}{2} x_{}^{2} + 2 x$ $- x + 5$
③当 x=-2 时， $- \frac{1}{2} x_{}^{2} + 2 x$ $- x + 5$

(2)、归纳：若x 取任意实数， $- \frac{1}{2} x_{}^{2} + 2 x$ 与 $- x + 5$ 有怎样的大小关系?试说明理由.

查看试题解析
14. 已知 $M = \frac{2}{9} a - 1 ， N = a^{2} - \frac{7}{9} a (a$ 为任意实数)，则M，N的大小关系为（）

A、M<N B、M=N C、M>N D、因为含有字母a，所以M，N的大小不能确定

查看试题解析
15. 设 $M = 2 a^{2} - 5 a + 1$ ， $N = 3 a^{2} + 7$ ，其中a为实数，则M与N的大小关系是（）

A、 B、 C、 D、不能确定．

查看试题解析
16. 已知3x﹣y＝3a²﹣6a+9，x+y＝a²+6a﹣10，当实数a变化时，x与y的大小关系是（）

A、x＞y B、x＝y C、x＜y D、x＞y、x＝y、x＜y都有可能

查看试题解析
17. 若 $M = 2 x^{2} - 12 x + 15$ ， $N = x^{2} - 8 x + 11$ ，则 $M$ 与 $N$ 的大小关系为．

查看试题解析
18. 设A＝a+3，B＝a²﹣a+5，则A与B的大小关系是AB（填“＞，＝，＜”之一）

查看试题解析
19. 阅读下列材料：
材料一“a²≥0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式.例如： $x^{2} + 4 x + 5 = x^{2} + 4 x + 4 + 1 = {(x + 2)}^{2} + 1 .$
$∵ {(x + 2)}^{2} \geq 0 ， ∴ {(x + 2)}^{2} + 1 \geq 1 ， ∴ x^{2} + 4 x + 5 \geq 1 .$
材料二我们在比较两个数或式的大小时常用“作差法”.
例如：若a-b>0，则a>b；a-b=0，则a=b；若a-b<0，则a<b.
解决下列问题：

(1)、填空： $x^{2} - 6 x + 10 =$ （x）²+（）

(2)、已知 $x^{2} - 2 x y + 2 y^{2} + 2 y + 1 = 0$ ，求x+y的值.

(3)、比较代数式 $x^{2} - 1$ 与2x-3的大小，并说明理由.

查看试题解析
20. 我们通常用作差法比较代数式大小.例如：已知M＝2x+3，N＝2x+1，比较M和N的大小.先求M﹣N，若M﹣N＞0，则M＞N；若M﹣N＜0，则M＜N；若M﹣N＝0，则M＝N，反之亦成立.本题中因为M-N＝（2x+3）-（2x+1）＝2＞0，所以M＞N.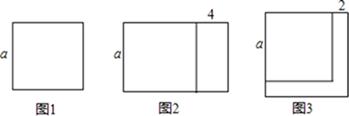

(1)、如图1是边长为a的正方形，将正方形一边不变，另一边增加4，得到如图2所示的新长方形，此长方形的面积为S₁；将图1中正方形边长增加2得到如图3所示的新正方形，此正方形的面积为S₂.用含a的代数式表示S₁＝， S₂＝（需要化简）.然后请用作差法比较S₁与S₂大小；

(2)、已知A＝2a²﹣6a+1，B＝a²﹣4a﹣1，请你用作差法比较A与B大小.

(3)、若M＝（a﹣4）² ， N＝16﹣（a﹣6）² ，且M＝N，求（a﹣4）（a﹣6）的值.

查看试题解析

三、类型3 求多项式的参数

21. 已知关于x的多项式 $- x^{2} + m x + 4$ 的最大值为5，则m的值可能为（）

A、1 B、2 C、3 D、4

查看试题解析
22. 请同学们学习材料①若 $x - y > 0$ ，则 $x > y$ ；② $x^{2} + x + 1 = (x^{2} + x + \frac{1}{4}) + \frac{3}{4} = {(x + \frac{1}{2})}^{2} + \frac{3}{4} ⩾ \frac{3}{4}$ ．解决以下问题： $A = x^{2} + 2 y^{2}$ ， $B = 2 x y + y - m$ ，当 $A > B$ 恒成立时， $m$ 的取值范围是（）

A、 $m > \frac{1}{4}$ B、 $m > \frac{1}{2}$ C、 $m > \frac{3}{4}$ D、 $m > 1$

查看试题解析
23. 已知方程 $x^{2} - 6 x + n = 0$ 可以配方成 ${(x - m)}^{2} = 7$ ，则 ${(m - n)}^{2023}$ 的值为（）

A、0 B、1 C、-1 D、 $2^{2023}$

查看试题解析
24. 用配方法解一元二次方程3x²+6x﹣1＝0时，将它化为（x+a）²＝b的形式，则a+b的值为（　　）

A、 $\frac{10}{3}$ B、 $\frac{7}{3}$ C、2 D、 $\frac{4}{3}$

查看试题解析
25. 将一元二次方程x²﹣8x﹣5＝0化成（x+a）²＝b（a ， b为常数）的形式，则a ， b的值分别是（　　）

A、﹣4，21 B、﹣4，11 C、4，21 D、﹣4，﹣21

查看试题解析

四、类型4 利用非负数的性质求值或证明

26. 把方程 x²+6x -5 = 0化成 (x+m)²=n的形式，则 m+n的值为（）

A、17 B、14 C、11 D、7

查看试题解析
27. 已知 $4 x^{2} - 4 x + 1 + \sqrt{3 y - 2} = 0$ 则x+y的值为（）

A、 $\frac{1}{6}$ B、 $\frac{7}{6}$ C、 $\frac{8}{3}$ D、 $- \frac{4}{3}$

查看试题解析
28.
试用配方法证明：代数式 $x^{2} - 2 x + 4$ 的值不小于3．

查看试题解析
29. 若实数x，y，z满足 $x = 4 - y ， z^{2} = x y - 4$ 求证：x=y.

查看试题解析
30. 已知A=a+2，B=2a²-3a+10，求证：无论a为何值，A<B恒成立．

查看试题解析
31. 用配方法求证：代数式 $3 x^{2} - 6 x + 7$ 的值恒为正数．

查看试题解析
32. 已知在△ABC中，三边长a，b，c满足 a²+2b²+c²−2ab-2bc=0，请判断△ABC的形状，并证明你的结论．

查看试题解析
33. （阅读材料）把形如ax²+bx+c的二次三项式（或其一部分）经过适当变形配成完全平方式的方法叫配方法，配方法在因式分解、证明恒等式、利用a²≥0求代数式最值等问题中都有广泛应用.
例如：利用配方法将x²﹣6x+8变形为a（x+m）²+n的形式，并把二次三项式分解因式.

配方：x²﹣6x+8

＝x²﹣6x+3²﹣3²+8

＝（x﹣3）²﹣1

分解因式：x²﹣6x+8

＝（x﹣3）²﹣1

＝（x﹣3+1）（x﹣3﹣1）

＝（x﹣2）（x﹣4）

（解决问题）根据以上材料，解答下列问题：

(1)、利用配方法将多项式x²﹣4x﹣5化成a（x+m）²+n的形式.

(2)、利用配方法把二次三项式x²﹣2x﹣35分解因式.

(3)、若a、b、c分别是 $△$ ABC的三边，且a²+2b²+3c²﹣2ab﹣2b﹣6c+4＝0，试判断 $△$ ABC的形状，并说明理由.

(4)、求证：无论x，y取任何实数，代数式x²+y²+4x﹣6y+15的值恒为正数.

查看试题解析