2024年浙教版数学八(下)微素养核心突破4 二次根式的相关计算
试卷更新日期:2024-04-14 类型:复习试卷
一、类型1 巧用乘方公式
-
1. 计算的结果是( )A、7 B、 C、 D、2. 若 , 则的值是.3. 如果为有理数),那么a= , b=.4. 已知 则代数式 的值为.5. 阅读与思考
请仔细阅读并完成相应任务:在解决问题“已知 , 求 的值”时,小明是这样分析与解答的:
∵
∴ ,
∴ ,
∴.
任务:请你根据小明的分析过程,解决如下问题:若 , 求的值.
6. 解答下列各题:(1)、计算: .(2)、设实数 的整数部分为a,小数部分为b,求 的值.二、类型2 整体代入
-
7. 已知 , , 则.8. 已知 , , 则的值是.9. 已知 , , 则=.10.(1)、已知x=2+ , y=2- , 求的值;(2)、已知a= , b= , 求a2-3ab+b2的值11. 已知 , 求 的值.12. 定义:我们将与称为一对“对偶式”,因为
, 所以构造“对偶式”再将其相乘可以有效的将中的“根号”去掉,于是二次根式除法可以这样计算:如.像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.
根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)、对偶式与之间的关系为____.A、互为相反数 B、互为倒数 C、绝对值相等 D、没有任何关系(2)、已知 , , 求的值.(3)、解方程:(提示:利用“对偶式”相关知识,令).三、类型3 数形结合
-
13. 要焊接一个如图所示的钢架,需要的钢材长度是( )
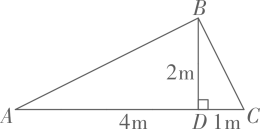 A、 B、 C、 D、14.(1)、填空:
A、 B、 C、 D、14.(1)、填空:,
,
, .
(2)、 定等于a吗? 你发现其中的规律了吗?请用自己的语言描述出来。(3)、利用你总结的规律,计算:①若
②
(4)、若a,b,c为三角形的三边长,化简:15. 我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积.用现代式子表示即为:s= (其中a、b、c为三角形的三边长,s为面积).若已知三角形的三边长分别为5,6,7,试运用公式计算该三角形的面积s.16. 已知 中, , , .(1)、分别化简 , ;(2)、试在4×4的方格纸上画出 ,使它的顶点都在方格的顶点上(每个小方格的边长为1);并求点B到 边的距离.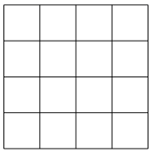 17. 如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.
17. 如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形. (1)、(i)已知点A在格点(即小正方形的顶点)上,画一条线段AB,长度为 ,且点B在格点上.
(1)、(i)已知点A在格点(即小正方形的顶点)上,画一条线段AB,长度为 ,且点B在格点上.(ii)以上题所画的线段AB为一边,另外两条边长分别为 , .画一个△ABC,使点C在格点上(只需画出符合条件的一个三角形).
(2)、所画出的△ABC的边AB上的高线长为 . (直接写出答案)四、类型4 先变形、再化简