2024年北师大版数学八年级下册周测卷(第六章第1-2节)培优卷
试卷更新日期:2024-04-14 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 在四边形ABCD中,将下列条件中的任意两个进行组合,可以判定它是平行四边形的有( )组.
(1)AB∥CD (2)AD∥BC(3)AB=CD(4)AD=BC(5)∠A=∠C(6)∠B=∠DA、7 B、8 C、9 D、102. 在下列给出的条件中,不能判定四边形ABCD为平行四边形的是( )A、 B、 C、 , D、3. 如图,在▱ABCD中,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,若△CDE的周长为8,则▱ABCD的周长为( )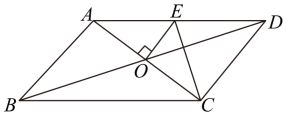 A、8 B、10 C、16 D、204. 在▱ABCD中,AC=24,BD=38,AB=m,则m的取值范围是( )A、24<m<39 B、14<m<62 C、7<m<31 D、7<m<125. 下列四组条件中,不能判定四边形ABCD为平行四边形的是( )A、AB=CD,AD=BC B、AB∥CD,AB=CD C、AB=CD,AD∥BC D、AB∥CD,AD∥BC6. 如图,四边是平行四边形, , 与的延长线交于点E,连接交于F,连接 , 下列结论中:①四边形是平行四边形;②;③若 , 则;④若 , 则是直角三角形,正确的结论有( )
A、8 B、10 C、16 D、204. 在▱ABCD中,AC=24,BD=38,AB=m,则m的取值范围是( )A、24<m<39 B、14<m<62 C、7<m<31 D、7<m<125. 下列四组条件中,不能判定四边形ABCD为平行四边形的是( )A、AB=CD,AD=BC B、AB∥CD,AB=CD C、AB=CD,AD∥BC D、AB∥CD,AD∥BC6. 如图,四边是平行四边形, , 与的延长线交于点E,连接交于F,连接 , 下列结论中:①四边形是平行四边形;②;③若 , 则;④若 , 则是直角三角形,正确的结论有( )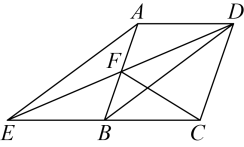 A、4 B、3 C、2 D、17. 下列命题不正确的是( )A、等腰三角形的两底角相等 B、平行四边形的对角线互相平分 C、角平分线上的点到角两边的距离相等 D、三个角分别对应相等的两个三角形全等8. 已知△ABC(如图1),按图2、图3所示的尺规作图痕迹,不需借助三角形全等,就能推出四边形ABCD是平行四边形的依据是( )
A、4 B、3 C、2 D、17. 下列命题不正确的是( )A、等腰三角形的两底角相等 B、平行四边形的对角线互相平分 C、角平分线上的点到角两边的距离相等 D、三个角分别对应相等的两个三角形全等8. 已知△ABC(如图1),按图2、图3所示的尺规作图痕迹,不需借助三角形全等,就能推出四边形ABCD是平行四边形的依据是( )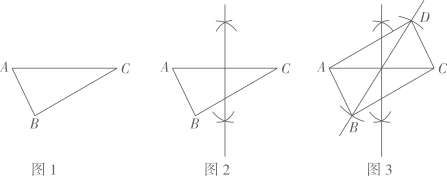 A、两组对边分别平行的四边形是平行四边形 B、对角线互相平分的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、两组对边分别相等的四边形是平行四边形9. 在平面直角坐标系中,已知四边形 各顶点坐标分别是: ,且 ,那么四边形 周长的最小值为( )A、 B、 C、 D、10. 在面积为的平行四边形ABCD中,分别过点A作直线BC的垂线AE,垂足为E,作直线CD的垂线AF,垂足为F.若AB= , BC= , 则CE+CF的值为( )A、 B、 C、或 D、或
A、两组对边分别平行的四边形是平行四边形 B、对角线互相平分的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、两组对边分别相等的四边形是平行四边形9. 在平面直角坐标系中,已知四边形 各顶点坐标分别是: ,且 ,那么四边形 周长的最小值为( )A、 B、 C、 D、10. 在面积为的平行四边形ABCD中,分别过点A作直线BC的垂线AE,垂足为E,作直线CD的垂线AF,垂足为F.若AB= , BC= , 则CE+CF的值为( )A、 B、 C、或 D、或二、填空题(每题3分,共18分)
-
11. 已知平行四边形ABCD中,AB=5,∠ABC与∠DCB的平分线分别交AD边于点E、F,且EF=3,则边AD的长为 .12. 如图,将沿翻折得到 , 若 , , 则的度数为.
 13. 如图所示的网格是正方形网格,点A,B,C,D是网格线交点,则△ABC的面积与△BCD的面积的大小关系为:S△ABCS△BCD(填“>”,“=”或“<”).
13. 如图所示的网格是正方形网格,点A,B,C,D是网格线交点,则△ABC的面积与△BCD的面积的大小关系为:S△ABCS△BCD(填“>”,“=”或“<”).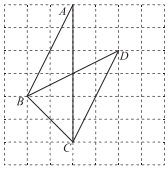 14. 如图,在▱ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4,则CE的长是 .
14. 如图,在▱ABCD中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4,则CE的长是 .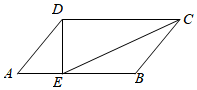 15. 如图,在中, , , 、分别平分、 , 则长为.
15. 如图,在中, , , 、分别平分、 , 则长为.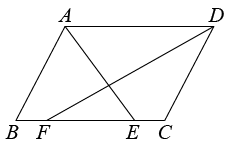 16. 如图,在平行四边形中,点是的中点,将沿直线翻折至平行四边形所在平面内,得到 , 连结 , 并延长 , 交于点 , 若 , , 则的长为 .
16. 如图,在平行四边形中,点是的中点,将沿直线翻折至平行四边形所在平面内,得到 , 连结 , 并延长 , 交于点 , 若 , , 则的长为 .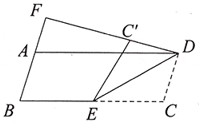
三、解答题(共7题,共72分)
-
17. 已知:如图,点E,F分别为的边BC,AD上的点,且.求证:.
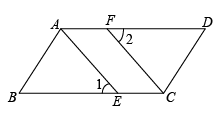 18. 如图,在三角形ABC中,AD⊥BC于点D , EF⊥BC于点F , ∠B=∠GDC . 请说明∠1=∠2的理由.
18. 如图,在三角形ABC中,AD⊥BC于点D , EF⊥BC于点F , ∠B=∠GDC . 请说明∠1=∠2的理由. 19. 如图,在 ABCD中,AE平分∠BAD交DC于点E,AD=6cm,AB=9cm,求EC的长.
19. 如图,在 ABCD中,AE平分∠BAD交DC于点E,AD=6cm,AB=9cm,求EC的长.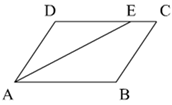 20. 如图,分别以的直角边及斜边向外作等边 , 等边 , 已知 , , 垂足为F,连接
20. 如图,分别以的直角边及斜边向外作等边 , 等边 , 已知 , , 垂足为F,连接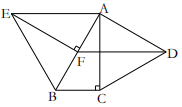 (1)、求证:;(2)、四边形是平行四边形吗?请说明理由.21. 在①;②;③这三个条件中任选一个补充在下面的横线上,并完成下面的证明.
(1)、求证:;(2)、四边形是平行四边形吗?请说明理由.21. 在①;②;③这三个条件中任选一个补充在下面的横线上,并完成下面的证明.如图,已知四边形ABCD是平行四边形,对角线AC,BD相交于点O,点E,F在AC上,连接BE,DF,BF,DE,且____(填写序号).
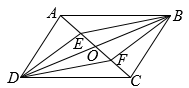 (1)、选择的条件的序号是;(2)、求证:;(3)、求证:四边形DEBF是平行四边形.22. 【教材呈现】下图是华师版八年级下册数学教材第83页和84页的部分内容.
(1)、选择的条件的序号是;(2)、求证:;(3)、求证:四边形DEBF是平行四边形.22. 【教材呈现】下图是华师版八年级下册数学教材第83页和84页的部分内容.平行四边形的判定定理2 一组对边平行且相等的四边形是平行四边形.
我们可以用演绎推理证明这一结论.
已知:如图,在四边形中,ABCD且 .
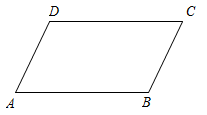
求证:四边形是平行四边形.
证明:连接 .
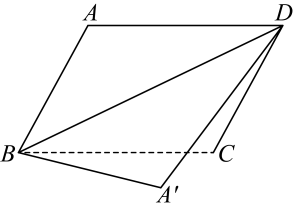
(1)、请根据教材提示,结合图,写出完整的证明过程.(2)、【知识应用】如图①,在中,延长到点 , 使 , 连接、 . 求证:四边形是平行四边形.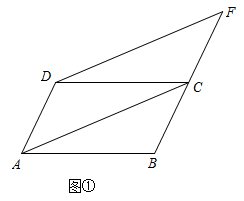 (3)、【拓展提升】在【知识应用】的条件下,若四边形的面积为7,直接写出四边形的面积.23. 【问题背景】
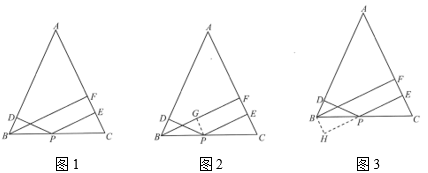
(3)、【拓展提升】在【知识应用】的条件下,若四边形的面积为7,直接写出四边形的面积.23. 【问题背景】某“数学学习兴趣小组”在学习了“等腰三角形的性质”和“平行四边形的性质和判定”后,在习题中发现了这样一个问题:如图1,在等腰中, , 点D、E分别是边上的点,点P是底边上的点,且 , 过点B作于点F,请写出线段、、之间满足的数量关系式.
同学们经过交流讨论,得到了如下两种解决思路:
解决思路1:如图2,过点P作于点G;
解决思路2:如图3,过点B作 , 交的延长线于点H;
 (1)、上述两种解决思路都可以证明一组三角形全等,判定一个四边形为平行四边形,从而可证得线段之间满足的数量关系式为 .(2)、【类比探究】
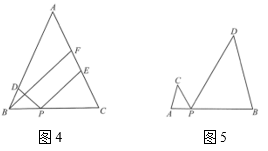
(1)、上述两种解决思路都可以证明一组三角形全等,判定一个四边形为平行四边形,从而可证得线段之间满足的数量关系式为 .(2)、【类比探究】如图4,在等腰中, , 点D、E分别是边上的点,点P是底边上的点,且 , 过点B作交于点F,请写出线段之间满足的数量关系式,并说明理由.
(3)、 【拓展应用】如图5,在与中, , , 点A、B、P在同一条直线上,若 , , 则 .