2024年北师大版数学八年级下册周测卷(第六章第1-2节)基础卷
试卷更新日期:2024-04-14 类型:同步测试
一、选择题(每题3分,共30分)
-
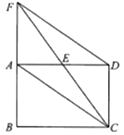
1. 如图,在中,对角线AC与BD相交于点O,则下列结论一定正确的是( )
 A、 B、 C、 D、2. 如图在▱ABCD中,已知AC=4cm,若△ACD的周长为13cm,则▱ABCD的周长为( )
A、 B、 C、 D、2. 如图在▱ABCD中,已知AC=4cm,若△ACD的周长为13cm,则▱ABCD的周长为( ) A、26cm B、24cm C、20cm D、18cm3. 如图,在▱ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长等于( )
A、26cm B、24cm C、20cm D、18cm3. 如图,在▱ABCD中,已知AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长等于( ) A、8cm B、6cm C、4cm D、2cm4. 综合实践课上,嘉嘉画出 , 利用尺规作图找一点C,使得四边形为平行四边形.图1~图3是其作图过程.
A、8cm B、6cm C、4cm D、2cm4. 综合实践课上,嘉嘉画出 , 利用尺规作图找一点C,使得四边形为平行四边形.图1~图3是其作图过程.(1)作的垂直平分线交于点O;
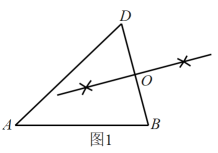
(2)连接 , 在的延长线上截取;
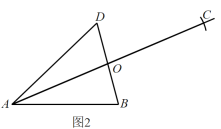
(3)连接 , , 则四边形即为所求.
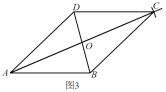
在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是( )
A、两组对边分别平行 B、两组对边分别相等 C、对角线互相平分 D、一组对边平行且相等5. 依据所标数据,下列一定为平行四边形的是()A、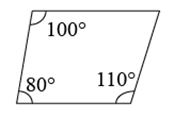 B、
B、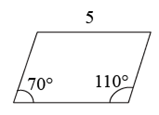 C、
C、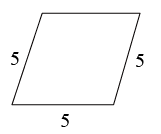 D、
D、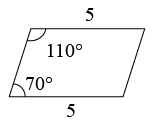 6. 顺次连接平面上A、B、C、D四点得到一个四边形,从①AB∥CD②BC=AD③∠A=∠C④∠B=∠D四个条件中任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况共有( )A、5种 B、4种 C、3种 D、1种7. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
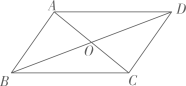
6. 顺次连接平面上A、B、C、D四点得到一个四边形,从①AB∥CD②BC=AD③∠A=∠C④∠B=∠D四个条件中任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况共有( )A、5种 B、4种 C、3种 D、1种7. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( ) A、①,② B、①,④ C、③,④ D、②,③8. 如图,在▱ABCD 中,AC 与 BD 相交于点O,∠ODA=90°,OA=6,OB=2,则AD的长是( )
A、①,② B、①,④ C、③,④ D、②,③8. 如图,在▱ABCD 中,AC 与 BD 相交于点O,∠ODA=90°,OA=6,OB=2,则AD的长是( )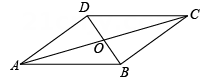 A、6 B、4 C、4 D、49. 如图,在四边形 ABCD中,对角线 AC 和 BD 相交于点O.下列条件中,不能判定四边形ABCD为平行四边形的是 ( )
A、6 B、4 C、4 D、49. 如图,在四边形 ABCD中,对角线 AC 和 BD 相交于点O.下列条件中,不能判定四边形ABCD为平行四边形的是 ( ) A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AB∥DC,AD=BC D、OA=OC,OB=O10. 在中,点D,E分别是 , 上的点,且 , 点F是延长线上一点,连接 . 添加下列条件后,不能判断四边形是平行四边形的是( )
A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AB∥DC,AD=BC D、OA=OC,OB=O10. 在中,点D,E分别是 , 上的点,且 , 点F是延长线上一点,连接 . 添加下列条件后,不能判断四边形是平行四边形的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 如图,在▱ABCD中,E,F分别在边 BC,AD 上,有以下条件:①AF=CF;②AE=CF;③∠BEA =∠FCE.若要使四边形AFCE 为平行四边形,则还需添加上述条件中的(填序号).
 12. 阅读下面材料:
12. 阅读下面材料:在数学课上,老师提出如下问题:
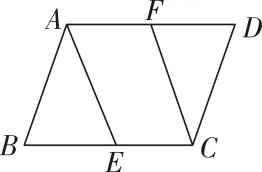
已知:如图1,及边的中点 , 求作:平行四边形 .
小静的作法如下:
在数学课上,老师提出如下问题:
①连接并延长,在延长线上截取;
②连接 . 所以四边形就是所求作的平行四边形.
老师说:“小静的作法正确”.
请回答:小静的作法正确的理由是 .
13. 如图,在▱ABCD中,过点C作CE⊥AB,交BA的延长线于点E.若∠EAD=40°,则∠BCE的度数为°.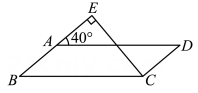 14. 如图,在▱中,的平分线交于点 , 的平分线交于点 , 若 , , 则的长是 .
14. 如图,在▱中,的平分线交于点 , 的平分线交于点 , 若 , , 则的长是 .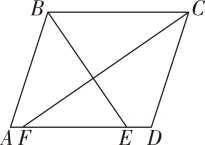 15. 如图,平行四边形中,对角线、相交于点 , 过点的直线分别交、于点、 , 若 , , , 则图中阴影部分的面积是 .
15. 如图,平行四边形中,对角线、相交于点 , 过点的直线分别交、于点、 , 若 , , , 则图中阴影部分的面积是 .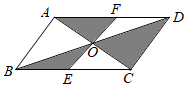 16. 如图,四边形是平行四边形,若 , , , 则 .
16. 如图,四边形是平行四边形,若 , , , 则 .
三、解答题(共8题,共72分)
-
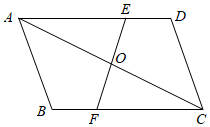
17. 如图,在 中,点 , 分别在 、 上,且 ,连接 , 交于点 .求证: .
 18. 如图,在平行四边形中,延长到点E,延长到点F,使 , 连接交边于点G,交边于点H.求证: .
18. 如图,在平行四边形中,延长到点E,延长到点F,使 , 连接交边于点G,交边于点H.求证: .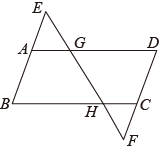 19. 如图,是四边形的对角线, , 垂足分别为E,F,且 . 证明:四边形为平行四边形.
19. 如图,是四边形的对角线, , 垂足分别为E,F,且 . 证明:四边形为平行四边形. 20. 如图,在四边形中, , , , ,
20. 如图,在四边形中, , , , ,
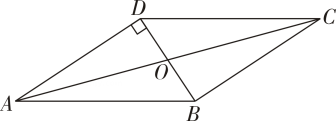 (1)、求证;四边形为平行四边形;
(1)、求证;四边形为平行四边形;
(2)、求四边形的面积.21. 如图,在平行四边形ABCD中,连接AC,∠ACB的角平分线CE交AB与点E,∠DAC的角平分线AF交CD于点F. (1)、如图1,求证:BE=DF;(2)、如图2,过点A作AH⊥BC,∠ACB=2∠BAH,在不添加任何辅助线和字母的情况下,请直接写出与∠BAH互余的角.
(1)、如图1,求证:BE=DF;(2)、如图2,过点A作AH⊥BC,∠ACB=2∠BAH,在不添加任何辅助线和字母的情况下,请直接写出与∠BAH互余的角.