2024年浙教版数学七（下）微素养核心突破8 整式运算的应用

试卷更新日期：2024-04-13 类型：复习试卷

进入出卷网下载

一、求图形的周长或面积

1. 如果长方形的长为( $(4 a^{2} - 2 a + 1) ，$ 宽为(2a+1)，那么这个长方形的面积为（）

A、8a³-4a²+2a-1 B、8a³+4a²-2a-1 C、8a³-1 D、8a³+1

查看试题解析
2. 有若干个大小形状完全相同的小长方形，现将其中4个如图1摆放，构造出一个正方形，其中阴影部分周长为24，其中6个如图2摆放，构造出一个长方形，其中阴影部分面积为102，则每个小长方形的面积为（）

A、4 B、6 C、8 D、10

查看试题解析
3. 有若干个大小、形状完全相同的小长方形，现将其中4个按如图1所示的方式摆放，构造出一个正方形，其中阴影部分的面积为40.再用5个按如图2所示的方式摆放，构造出一个长方形，其中阴影部分的面积为100(各个小长方形之间不重叠不留空)，则每个小长方形的面积为（）

A、5 B、10 C、20 D、30

查看试题解析
4. 如果一个长方形的周长为10，其中长为a，那么该长方形的面积为（　　）

A、10a B、5a﹣a² C、5a D、10a﹣a²

查看试题解析
5. 现有若干张边长为a的正方形A型纸片，边长为b的正方形B型纸片，长宽为a、b的长方形C型纸片，小明同学选取了1张A型纸片，4张B型纸片，4张C型纸片拼成了一个四边形，则此四边形的周长为．（用a、b代数式表示）

查看试题解析
6. 如图所示，在长方形 $A B C D$ 中，横向涂色部分是长方形，另一涂色部分是平行四边形，则空白部分的面积是（）

A、 $b c - a b + a c + c^{2}$ B、 $a b - b c - a c + c^{2}$ C、 $a^{2} + a b + b c - a c$ D、 $b^{2} - b c + a^{2} - a b$

查看试题解析
7. 当我们利用两种不同的方法计算同一图形的面积时，可以得到一个等式．例如，由图1，可得等式：(a＋2b)(a＋b)＝a²＋3ab＋2b² ．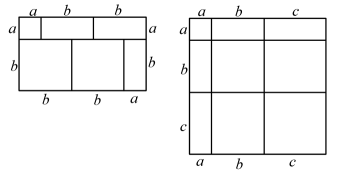

图1 图2

(1)、根据图2，可得等式：．

(2)、利用题(1)所得结论解决问题：已知a＋b＋c＝12，ab＋bc＋ac＝47，求a²＋b²＋c²的值；

查看试题解析
8. 热爱数学的小明在家中发现了一根铁丝，他先把该铁丝做成如图甲的长方形，再把该铁丝做成如图乙的长方形，它们的边长如图所示，面积分别为_{$S_{1}$} ， _{$S_{2}$}.

(1)、请计算甲，乙长方形的面积差.

(2)、若把该铁丝做成一个正方形，该正方形的面积为_{$S_{3}$}. 已知_{$S_{1} + S_{2} = \frac{3}{2} S_{3}$} ，求_{$S_{3}$}的值.

查看试题解析
9. 先将一张边长为a的正方形纸片按如图1所示的方式放置于长方形 ABCD内，再将长为 b(b $\frac{1}{2}$ b 的长方形纸片按如图2，3所示的两种方式放置，长方形 ABCD未被覆盖的部分用阴影表示，设图2 中阴影部分的面积为 S₁ ，图3中阴影部分的面积为 S₂ ，且S₂-S₁=2b，则AD-AB的值为（）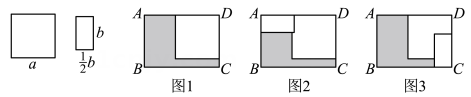

A、1 B、2 C、4 D、5

查看试题解析
10. 在长方形ABCD内，将两张边长分别为a和b（a>b）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），长方形中未被这两张正方形纸片覆盖的部分用阴影表示，若图1中阴影部分的面积为 S₁，图2中阴影部分的面积和为 S₂，则关于 S₁，S₂的大小关系表述正确的是（）

A、 $S_{1} > S_{2}$ B、 $S_{1} < S_{2}$ C、 $S_{1} = S_{2}$ D、 $S_{1} \geq S_{2}$

查看试题解析
11. 如图，将两张边长分别为 $a$ 和 $b$ （ $a > b$ ）的正方形纸片按图1，图2两种方式放置长方形内（图1，图2中两张正方形纸片均有部分重叠），未被这两张正方形纸片覆盖的部分用阴影表示，若长方形中边 $A B 、 A D$ 的长度分别为 $m 、 n$ ．设图1中阴影部分面积为 $S_{1}$ ，图2中阴影部分面积为 $S_{2}$ ．当 $m - n = 3$ 时， $S_{1} - S_{2}$ 的值为（）

A、3b B、 $3 a - 3 b$ C、 $3 a$ D、 $- 3 b$

查看试题解析
12. 在长方形ABCD内，将一张边长为a的正方形纸片和两张边长为b的正方形纸片（ $a > b$ ），按图1，图2两种方式放置（两个图中均有重叠部分），矩形中未被这三张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为 $s_{1}$ ，图2中阴影部分的面积为 $s_{2}$ ，当 $A D - A B = 2$ 时，若知道下列条件，能求 $s_{1} - s_{2}$ 值的是（）

A、边长为a的正方形的面积 B、边长为b的正方形的面积 C、边长为a的正方形的面积与两个边长为b的正方形的面积之和 D、边长a与b之差

查看试题解析
13. 如图，在长方形ABCD中，AB=6，BC=10，其内部有边长为a的正方形AEFG与边长为b的正方形HIJK，两个正方形的重合部分也为正方形，且面积为5.若右侧阴影部分的面积S₂是左侧阴影部分面积S₁的4倍，则正方形AEFG与正方形HIJK的面积之和为（）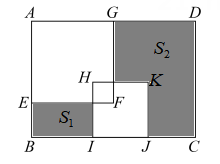

A、20 B、25 C、 $\frac{49}{2}$ D、 $\frac{81}{4}$

查看试题解析
14. 如图，把五个长为b，宽为a（b>a)的小长方形，按图一和图二两种方式放在一个长比宽大 $(6 - a)$ 的大长方形上，设图一中两块阴影部分的周长和为 $C_{1}$ ，图2中阴影部分的周长和为 $C_{2}$ ，则 $C_{2} - C_{1}$ 的值为.

查看试题解析
15. 如图有两张正方形纸片A和B ，图1将B放置在A内部，测得阴影部分面积为2，图2将正方形AB并列放置后构造新正方形，测得阴影部分面积为20，若将3个正方形A和2个正方形B并列放置后构造新正方形如图3，（图2，图3中正方形AB纸片均无重叠部分）则图3阴影部分面积（）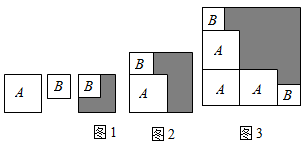

A、22 B、24 C、42 D、44

查看试题解析

二、结合乘法公式

16. 如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的长方形.根据图形的变化过程写出的一个正确的等式为（）

A、 $a^{2} - 2 a b + b^{2} = (a - b)^{2}$ B、 $a^{2} - a b = a (a - b)$ C、 $a^{2} - b^{2} = (a - b)^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
17. 如图是利用割补法求图形面积的示意图，下列公式中与之相对应的是（）

A、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ B、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$ C、 $(a + b) (a - b) = a^{2} - b^{2}$ D、 $(a b)^{2} = a^{2} b^{2}$

查看试题解析
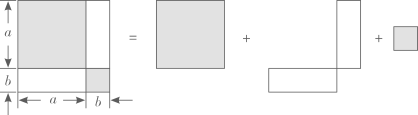18. 如图，两个正方形的边长分别为a，b，如果a+b=7，ab=11，那么阴影部分的面积为（）

A、24 B、16 C、9 D、8

查看试题解析
19. 已知 $x^{2} + 4 y^{2} = 13$ ， $x y = 3$ ，求 $x + 2 y$ 的值，这个问题我们可以用边长分别为 $x$ 和 $y$ 的两种正方形组成一个图形来解决，其中 $x > y$ ，能较为简单地解决这个问题是图形是（）

A、 B、 C、 D、

查看试题解析
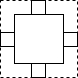20. 如图，将图1中 $L$ 形的纸片进行如图2的前拼，改造成了一个长方形，通过拼接前后两个图形的面积关系可以验证的等式是（）

A、 $4 a + 4 b = 4 (a + b)$ B、 $4 a b = (a + b)^{2} - (a - b)^{2}$ C、 $2 a b = (a + b)^{2} - (a^{2} + b^{2})$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
21. 如图，阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后得到的图形，小佳将阴影部分通过剪拼，拼成了图①、图②、图③三种新的图形，其中能够验证平方差公式的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
22. 如图，正方形ABCD和长方形DEFG的面积相等，且四边形AEFH也为正方形．欧几里得在《几何原本》中利用该图得到了：AH²＝AB×BH ．设AB＝a ， BH＝b ．若ab＝80，则图中阴影部分的周长为（）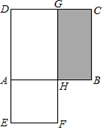

A、40 B、45 C、50 D、60

查看试题解析
23. 如图，为了美化校园，某校要在面积为30平方米长方形空地 $A B C D$ 中划出长方形 $E B K R$ 和长方形 $Q F S D$ ，若两者的重合部分 $G F H R$ 恰好是一个边长为3米的正方形，现将图中阴影部分区域作为花圃，若长方形空地 $A B C D$ 的长和宽分别为 $m$ 和 $n$ ， $m > n$ ，花圃区域 $A E G Q$ 和 $H K C S$ 总周长为14米，则m-n的值为（）

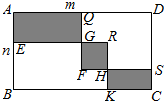A、 $4$ 米 B、 $7$ 米 C、 $5$ 米 D、 $3.5$ 米

查看试题解析
24. 如图，边长为6的正方形ABCD中放置两个长和宽分别为a，b的长方形，若长方形的周长为 16，面积为 15.75，则图中阴影部分的面积 $S_{1} + S_{2} + S_{3}$ =.

查看试题解析
25. 如图，将一张长方形纸板按图中虚线裁剪成九块，其中有两块边长都为m的大正方形，两块边长都为n的小正方形，五块长为m，宽为n的小长方形．若每块小长方形的面积为7，四块正方形的面积和为100，则这个长方形纸板的周长为．

查看试题解析
26. 某中学开展“筑梦冰雪，相约冬奥”的学科活动，设计几何图形作品表达对冬奥会的祝福.小冬以长方形ABCD的四条边为边向外作四个正方形，设计出“中”字图案，如图所示.若四个正方形的周长之和为32，面积之和为12，则长方形ABCD的面积为 .

查看试题解析
27. 如图4张长为a、宽为b（a＞b）的长方形纸片，按如图的方式拼成一个边长为（a+b）的正方形，图中空白部分的面积为S₁ ，阴影部分的面积为S₂ ．若S₁＝2S₂ ，则a：b=（）

A、3：2 B、5：2 C、2：1 D、3：1

查看试题解析
28. 两个边长分别为a、b（a>b）的正方形如图（1）放置，现在取BD的中点P，连接PA、PE，如图（2），把图形分割成三部分，分别标记①、②、③，对应的图形面积分别记为 $S_{①}$ 、 $S_{②}$ 、 $S_{③}$ .

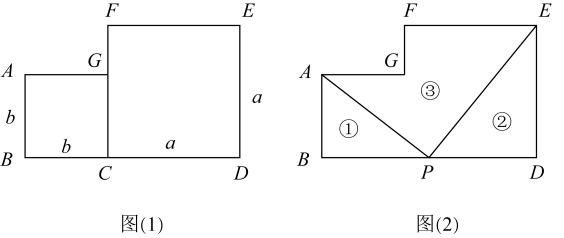(1)、用字母a、b分别表示 $S_{①}$ 、 $S_{②}$ .

(2)、若 $a - b = 2$ ， $a b = 15$ ，求 $S_{①} + S_{②}$ .

(3)、若 $S_{①} + S_{②} = 3$ ， $a b = 1$ ，求 $S_{③}$ .

查看试题解析
29. （1）请用两种不同的方法表示图中阴影部分的面积和.
方法1：____；
方法2：____.

(1)、请你直接写出三个代数式： ${(a + b)}^{2}$ ， $a^{2} + b^{2}$ ， ab之间的等量关系.

(2)、根据（2）中的等量关系，解决如下问题：
①已知 $m + n = 5$ ， $m^{2} + n^{2} = 20$ ，求mn和 ${(m - n)}^{2}$ 的值；
②已知 ${(x - 2021)}^{2} + {(x - 2023)}^{2} = 74$ ，求 ${(x - 2022)}^{2}$ 的值.

查看试题解析
30. 我们知道对于一个图形，通过不同的方法计算图形的面积可以得到一个数学等式.例如：由图1可得到 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

(1)、写出由图2所表示的数学等式：.

(2)、根据上面的等式，如果将 $a - b$ 看成 $a + (- b)$ ，直接写出 ${(n - \frac{1}{n} + 1)}^{2}$ 的展开式（结果化简）；若 $n^{2} + \frac{1}{n^{2}} = 6$ ，求 ${(n - \frac{1}{n} + 1)}^{2}$ 的值.

(3)、已知实数a、b、c，满足以下两个条件： $a^{2} + b^{2} + c^{2} + 2 a - 4 b + 6 c = - 10$ 且 $(a + 1) (c + 3) + (b - 2) (c + 3) = (a + 1) (b - 2)$ ，求 $a + b - c$ 的值.

查看试题解析

三、实际应用

31. 某厂原来生产一种边长为a厘米的正方形地砖，现将地砖的一边扩大3厘米，另一边缩短3厘米，改成生产长方形地砖.若材料的成本价为每平方厘米b元，则这种长方形地砖每块的材料成本价与正方形地砖相比（）

A、增加了9b元 B、增加了3ab元 C、减少了9b元 D、减少了3ab元

查看试题解析
32. 某校操场原来的长是2x米，宽比长少 10米，现在把操场的长与宽都增加了 5米，则整个操场的面积增加了平方米.

查看试题解析
33. 一套房子的平面结构图如图所示(单位：m)．

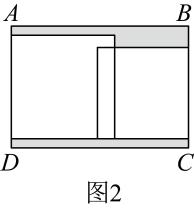
(1)、这套房子的主人打算把卧室以外的部分都铺上地砖，至少需要m² 的地砖．如果该种地砖的价格是a元/平方米，那么购买地砖至少需要元．

(2)、已知房屋的高度为h(m)，现需要在客厅和卧室的墙上贴壁纸，那么至少需要m²的壁纸．如果某种壁纸的价格是b元/平方米，那么购买壁纸至少需要元(计算时不扣除门、窗所占的面积)．

查看试题解析
34. 如图，要设计一幅长为(6x+4y)厘米，宽为(4x+2y)厘米的长方形图案，其中两横两竖涂上阴影，阴影部分的宽均为x厘米．

(1)、阴影部分的面积是多少平方厘米？(用含x，y的代数式表示)

(2)、空白区域的面积是多少平方厘米？(用含x，y的代数式表示)

查看试题解析
35. 学校为迎接艺术节，准备在一个正方形空地 $A B C D$ 上搭建一个表演舞台，如图所示，正中间是“红五月”三个正方形平台．其中“五”字正方形和“月”字正方形边长均为a米，“红”字正方形边长为b米．Ⅰ号区域布置造型背景，Ⅱ号区域设置为乐队演奏席．

(1)、用含a，b的代数式表示阴影部分的面积（即Ⅰ和Ⅱ面积之和）并化简；

(2)、若阴影部分的面积（即Ⅰ和Ⅱ面积之和）为288平方米，且 $a + b = 20$ 米，求“红”字正方形边长b的值．

查看试题解析
36. 现要在长方形草坪中规划出3块大小，形状一样的小长方形（图中阴影部分）区域种植鲜花.

(1)、如图1，大长方形的相邻两边长分别为 $60 m$ 和 $45 m$ ，求小长方形的相邻两边长.

(2)、如图2，设大长方形的相邻两边长分别为 $a$ 和 $b$ ，小长方形的相邻两边长分别为 $x$ 和 $y$ .
①1个小长方形的周长与大长方形的周长的比值是否为定值？若是，请求出这个值；若不是，请说明理由.

②若种植鲜花的面积是整块草坪面积的 $\frac{1}{2}$ ，求 $x$ 和 $y$ 满足的关系式（不含a，b）.

查看试题解析
37. 同学们一起布置艺术节活动现场，现在有一个边长为a的大正方形固定场地，以及四个边长为b的小正方形活动场地，设计如图1所示的阴影部分为展览区，其面积为S₁；如图2所示的阴影部分为竞赛区，其面积为S₂ ．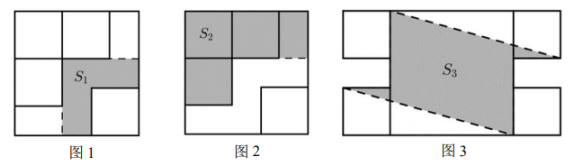

(1)、用含a，b的代数式分别表示S₁、S₂ ．

(2)、若a+b＝17，a²+b²=169，求S₁+S₂的值．

(3)、如图3，在（2）的基础上，将四个活动区域外移，形成的阴影部分为表演场地，其面积为S₃ ，求S₃的值．

查看试题解析

四、规律性问题

38. 在数学中，为了书写方便，我们记 $\sum_{k = 1}^{n} k = 1 + 2 + 3 + ... + (n - 1) + n,$ ， $\sum_{k = 1}^{n} (x + k) = (x + 1) + (x + 2) + ... + (x + n - 1) + (x + n)$ 则简化 $\sum_{k = 1}^{3} [(x - k) (x - k - 1)]$ 的结果是（）

A、 $3 x^{2} - 12 x - 9$ B、 $3 x^{2} - 9 x + 8$ C、 $3 x^{2} - 6 x - 20$ D、 $3 x^{2} - 15 x + 20$

查看试题解析
39. 观察下列等式：
$3^{2} - 4 \times 1^{2} = 5 ，$ ①
$5^{2} - 4 \times 2^{2} = 9 ，$ ②
$7^{2} - 4 \times 3^{2} = 13 ， ③$
……
寻找规律并解决下列问题：

(1)、完成第四个等式：9² $-$ 4×=.

(2)、写出你猜想的第 n个等式（用含 n的代数式表示），并验证其正确性.

查看试题解析
40. 阅读材料，回答下列问题：
2021×20202020-2020×20212021=？
分析可知，解决这个问题时，直接计算比较复杂，可尝试用x代替2021，y代替2020．
解：令2021=x ，2020=y，则
原式=x(y·10⁴+y)-y(x·10⁴+x)=xy·10⁴+xy-xy·10⁴-xy=0．
请回答下列问题：

(1)、在上述材料中，解决问题时体现了思想．

(2)、计算： $(1 - \frac{1}{2} - \frac{1}{3} - . . . - \frac{1}{2020}) (\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + . . . + \frac{1}{2021}) - (1 - \frac{1}{2} - \frac{1}{3} - . . . - \frac{1}{2021}) (\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + . . . + \frac{1}{2020})$

查看试题解析
41. 观察下列各式：
$(x - 1) (x + 1) = x^{2} - 1$ ； $(x - 1) (x^{2} + x + 1) = x^{3} - 1$ ； $(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$ ；
……
根据这一规律计算：

(1)、 $(x - 1) (x^{4} + x^{3} + x^{2} + x + 1) =$ ， $(x - 1) (x^{n} + x^{n - 1} + x^{2} + ⋯ x + 1) =$ ；

(2)、 $2^{2022} + 2^{2021} + 2^{2020} + \dots + 2^{2} + 2 + 1$ ；

(3)、 $3^{2022} - 3^{2021} + 3^{2020} - 3^{2019} + \dots + 3^{2} - 3 + 1$ .

查看试题解析
42. 观察下列各式：
(x-1)(x+1)=x²-1，
(x-1)(x²+x+1)=x³-1，
(x-1)(x³+x²+x+1)=x⁴-1，
……

(1)、填空：(x-1)() =x⁵-1．

(2)、根据规律可得(x-1) (x^n-1+……+x+1)=(其中n为正整数) ．

(3)、计算： (3-1) (3⁵⁰+3⁴⁹+3⁴⁸+……+3²+3+1)．

(4)、计算： (-2)²⁰²⁰+(-2)²⁰¹⁹+(-2)²⁰¹⁸+……+(-2)³+(-2)²+(-2)+1．

查看试题解析
43. 如图1，我们在某月的日历中标出一个十字星，并计算它的“十字差”(先将十字星左右两数，上下两数分别相乘，再将所得的积作差，即为该十字星的“十字差”)，则该十字星的“十字差”为12×14-6×20=48，再选择其他位置的十字星，可以发现“十字差”仍为48.

(1)、如图2，将正整数依次填入5列的长方形数表中，探究不同位置十字星的“十字差”，可以发现相应的“十字差”也是一个定值，这个定值为.

(2)、若将正整数依次填入6列的长方形数表中，不同位置十字星的“十字差”是一个定值吗? 如果是，请求出这个定值；如果不是，请说明理由.

(3)、若将正整数依次填入k列的长方形数表中(k≥3)，继续前面的探究，可以发现相应的“十字差”只与列数k有关，请用含 k的代数式表示出这个“十字差”，并说明理由.

查看试题解析