2024年浙教版数学七（下）微素养核心突破5 巧用平移变换解决问题
试卷更新日期：2024-04-13 类型：复习试卷
一、利用平移求线段长度和角度大小
-
1. 如图，向右平移2cm得到 ， 如果四边形的周长是20cm，那么的周长是（ ）
A、14cm B、16cm C、18cm D、20cm2. 如图，三角形ABC沿BC 所在的直线平移到三角形DEF 的位置，且C是线段BE的中点.若AB=5，BC=2，AC=4，则AD的长为 （ ）
A、5 B、4 C、3 D、23. 如图，△DAF沿直线AD平移得到△CDE，CE，AF的延长线交于点B．若∠AFD=111°，则∠CED=（ ）
A、110° B、111° C、112° D、113°4. 小温同学在美术课上将△ABC通过平移设计得到“一棵树”，已知底边AB上的高CD为5cm，沿CD方向向下平移3cm到△A1B1C1的位置，再经过相同的平移到△A2B2C2的位置，下方树干EF长为6cm，则树的高度CF长为（ ）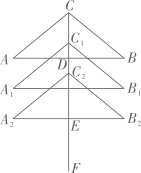
A、19 B、17 C、15 D、115. 如图，将直角 沿边 的方向平移到 的位置，连接 ，若 ，则 的长为（ ）
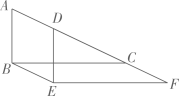A、3 B、4 C、5 D、66. 如图是某公园里一处矩形风景欣赏区 ， 长米，宽米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为1米，那小明沿着小路的中间，从出口A到出口B所走的路线（图中虚线）长为 ．
7. 如图，将△ABC沿水平方向向右平移到△DEF的位置，已知点A、D之间的距离为1，CE=3，则BF的长为 ．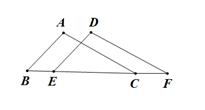
8. 一建筑物楼梯样式如图所示，经测量得出AB=3dm，BC=4dm，∠B=90°，CD=1dm，DE=1.5dm，EF=DE，AC=2AG．根据这些数据，试着计算出折线AC（即楼梯表面AJIHGFEDC）的长度为 ．
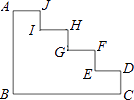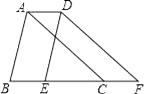
9. 如图，在四边形ABCD中，AD∥BC，且AD<BC，△ABC平移到△DEF的位置.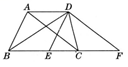
(1)、指出平移的方向和平移的距离；(2)、试说明AD+BC=BF.10. 如图，在Rt△ABC中，∠C=90°，∠A=33°，将△ABC沿AB方向向右平移得到△DEF．
(1)、试求出∠E的度数；(2)、若AE=9cm，DB=2cm．请求出CF的长度．二、利用平移求图形周长
-
11. 如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为（ ）
A、16cm B、18cm C、20cm D、22cm12. 将大小不一的正方形纸片①、②、③、④放置在如图所示的长方形ABCD内（相同纸片之间不重叠），其中AB＝a.小明发现：通过边长的平移和转化，阴影部分⑤的周长与正方形①的边长有关，那么阴影部分⑥与阴影部分⑤的周长之差与正方形（ ）（填编号）的边长有关.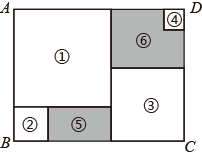
A、① B、② C、③ D、④13. 某景点拟在如图的长方形荷塘上架设小桥，若荷塘中小桥的总长为100 m，则荷塘周长为
14. 如图，Rt△AOB的周长为100，在其内部有n个小直角三角形，则这n个小直角三角形的周长之和为
15. 如图，在三角形中， ， ， ， ， 将三角形沿方向平移 得到三角形 ， 且与相交于点 ， 连接 ， 则阴影部分的周长为 ．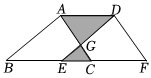
16. 如图，长方形ABCD与长方形BEFG等长等宽．若将长方形BEFG向右平移，距离为EF，长方形ABCD向右平移，距离为3个BC，则恰好构成新长方形AEPQ．若AEPQ的周长为56，求长方形AEPQ的面积．
17.如图，五边形ABCDE的每条边所在直线沿该边垂直方向向外平移4个单位，得到新的五边形A′B′C′D′E′．
（1）图中5块阴影部分即四边形AHA′G、BFB′P、COC′N、DMD′L、EKE′I能拼成一个五边形吗？说明理由；
（2）证明五边形A′B′C′D′E′的周长比五边形ABCD正的周长至少增加25个单位．
18. 如图，在三角形中， ， ， 沿方向平移至 ， 若 ， ．
(1)、求的长；(2)、求四边形的周长．19. 如图是一个多边形钢板ABCDEFGH，已知AB∥GH∥FE∥CD，BC∥DE∥AH∥GF，且BC=2EF，EF比CD长3cm，BC比CD长7cm，则这个多边形钢板的周长为cm。
20. 如图，是一块从一个边长为25cm的正方形BCDM材料中剪出的垫片，经测得FG＝8cm，则这个剪出的图形的周长是cm．
三、利用平移求图形面积
-
21. 如图，两个直角三角形重叠在一起，将其中一个沿点B到点C的方向平移到的位置， ， ， ， 平移距离为6，则阴影部分的面积为（ ）
A、40 B、42 C、45 D、4822. 如图，某居民小区有一长方形区域，居民想在长方形区城内修筑同样寬的两条小路，余下部分绿化，道路的宽为2m，则绿化的面积为多少平方米？
23. 如图，已知△ABC中，∠ABC＝90°，边BC＝12cm，把△ABC向下平移至△DEF后，AD＝5cm，GC＝4cm，请求出图中阴影部分的面积．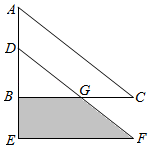
24. 如图，三角形ABC的边BC长为4cm.将三角形ABC平移2cm得到三角形A'B'C'，且BB'⊥BC，则阴影部分的面积为cm².
25. 如图，正方形ABCD先向右平移1个单位长度，再向上平移1个单位长度，得到正方形A'B'C'D'，形成了中间深色的正方形及四周空白的边框，已知正方形ABCD的面积为16．则四周空白边框的面积是
26. 如图所示，在一块长为30米，宽为16米的长方形草地上，有两条宽都为1米的纵、横相交的小路，这块草地的绿地面积为平方米．
27. 如图，在三角形ABC中，BC＝6，把三角形ABC延射线AB方向平移3个单位至三角形EFG处，EG与BC交于点M ． 若CM＝2，则图中阴影部分的面积为 ．
28. 如图，两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起，固定三角形ABC不动，将三角形DEF向右平移，当点E和点C重合时，停止移动，设DE交AC于G.给出下列结论：①四边形ABEG的面积与CGDF的面积相等；②AD∥EC，且AD＝EC；③若BF=8cm，EC=2cm，那么三角形DEF向右平移了2cm，则上述说法正确的个数为（ ）
A、0个 B、1个 C、2个 D、3个29. 如图，长方形ABCD的长AB为8，宽AD为6，将这个长方形向上平移3个单位，再向左平移2个单位，得到长方形EFGH，则阴影部分的面积为（ ）
A、30 B、32 C、36 D、4030. 将直角三角形ABC沿CB方向平移BE的距离后，得到直角三角形DEF，已知AG＝4，BE＝7，DE＝10，则阴影部分的面积 ．
31. 如图，在一块长为30米，宽为16米的长方形草地上，有两条宽都为1米的纵、横相交的小路，这块草地的绿地面积为平方米．
32. 如图，在 和 中， ， ， .若 的面积为 ，则 的面积为 .
33. 如图，将长为6，宽为4的长方形ABCD先向右平移2，再向下平移1，得到长方形A'B'CD'，则阴影部分的面积为 ．
34. 如图，将直径为的半圆水平向左平移 ， 则半圆所扫过的面积（阴影部分）为 ．
35. 如图
(1)、动手操作如图1，在的网格中，将线段向右平移，得到线段 ， 连接 ， ．①线段平移的距离是；
②四边形的面积；
(2)、如图2，在的网格中，将折线向右平移3个单位长度，得到折线 ．①画出平移后的折线；
②连接 ， ， 多边形的面积 ▲ ；
(3)、拓展延伸如图3，在一块长为米，宽为米的长方形草坪上，修建一条宽为米的小路（小路宽度处处相同），直接写出剩下的草坪面积 ．36. 某公园有很多的长方形草地，草地里修了很多有趣．的小路，如图三个图形都是长为50米，宽为30米的长方形草地，且小路的宽都是1米．
(1)、如图1，阴影部分为1米宽的小路，长方形除去阴影部分后剩余部分为草地，则草地的面积为平方米；(2)、如图2，有两条宽均为1米的小路(图中阴影部分)，则草地的面积为平方米；(3)、如图3，非阴影部分为1米宽的小路，沿着小路的中间从人口E处走到出口F处，所走的路线(图中虚线)长为米。37. 如图①，将线段A1A2向右平移1个单位到B1B2 ， 得到封闭图形A1A2B2B1(即阴影部分)，在图②中，将折线A1A2A3向右平移1个单位到B1B2B3 ， 得到封闭图形A1A2A3B3B2B1(即阴影部分)。
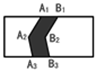
（图①）（图②）（图③）
(1)、在图③中，请你类似地画一条有两个折点的折线，同样向右平移1个单位，从而得到一个封闭图形，并用阴影表示；(2)、请你分别写出上述三个图形中除去阴影部分后剩余部分的面积(设长方形水平方向长均为a，竖直方向长均为b)：S1=，S2=，S3=；(3)、如图④，在一块长方形草地上，有一条弯曲的小路（小路任何地方的水平宽度都是2个单位），请你求出空白部分表示的草地面积是多少？
（图④）（图⑤）
(4)、如图⑤，若在（3）中的草地又有一条横向的弯曲小路（小路任何地方的宽度都是1个单位），请你求出空白部分表示的草地的面积是多少？38. 图中的四个长方形水平方向的边长均为a，竖直方向的边长均为b，且a>b>1.在图1中将线段A1A2向右平移1个单位到B1B2 ， 得到封闭图形A1A2B2B1(阴影部分).在图2中，将折线A1A2A3向右平移1个单位到折线B1B2B3 ， 得到封闭图形A1A2A3B3B2B1(阴影部分).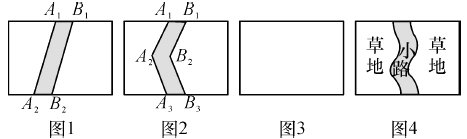
(1)、在图3中，请类似地画一条有两个折点的折线，同样向右平移1个单位，从而得到一个封闭图形，并在这个图形内涂上阴影；(2)、请你分别写出上述三个图形去掉阴影部分后剩余部分的面积：S1= ， S2= ， S3=；(3)、联想与操作：如图4，在一块长方形草地上，有一条弯曲的柏油小路(小路的任何地方水平宽度都是1个单位)请你猜想，空白部分表示的草地面积是多少？并说明理由.