2024年浙教版数学七(下)微素养核心突破4 平行线的判定与性质-折叠问题
试卷更新日期:2024-04-13 类型:复习试卷
一、选择题
-
1. 一条两边沿互相平行的围巾按图甲所示折叠并将其绘制成图乙,已知 , 且 , 则( )
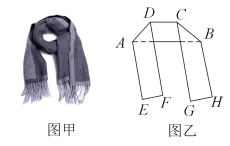 A、 B、 C、 D、2. 将长方形ABCD纸片沿AE折叠,得到如图所示的图形,已知∠CED'=80°,则∠EAB的大小是( )
A、 B、 C、 D、2. 将长方形ABCD纸片沿AE折叠,得到如图所示的图形,已知∠CED'=80°,则∠EAB的大小是( )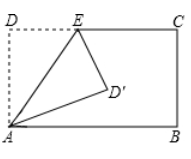 A、60° B、50° C、75° D、55°3. 学习平行线后,张明想出了过已知直线外一点画这条直线的平行线的新方法,他是通过折一张半透明的纸得到的.观察图(1)~(4),经两次折叠展开后折痕CD所在的直线即为过点P与已知直线a平行的直线.由操作过程可知张明画平行线的依据有( )
A、60° B、50° C、75° D、55°3. 学习平行线后,张明想出了过已知直线外一点画这条直线的平行线的新方法,他是通过折一张半透明的纸得到的.观察图(1)~(4),经两次折叠展开后折痕CD所在的直线即为过点P与已知直线a平行的直线.由操作过程可知张明画平行线的依据有( )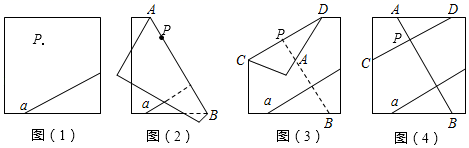
①同位角相等,两直线平行;
②两直线平行,同位角相等;
③内错角相等,两直线平行;
④同旁内角互补,两直线平行.
A、①③ B、①②③ C、③④ D、①③④4. 在数学拓展课《折叠的奥秘》中,老师提出一个问题:如图,有一条宽度相等的长方形纸带,将纸条沿折叠一下,若 , 则的度数为( )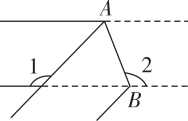 A、 B、 C、 D、5. 如图所示,把长方形沿折叠,若 , 则的度数为( )
A、 B、 C、 D、5. 如图所示,把长方形沿折叠,若 , 则的度数为( )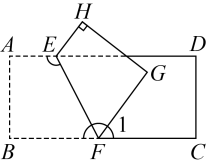 A、 B、 C、 D、6. 如图,把一张对边互相平行的纸条折叠,是折痕,若 , 下列结论:①;②;③;④ , 其中正确的有( )
A、 B、 C、 D、6. 如图,把一张对边互相平行的纸条折叠,是折痕,若 , 下列结论:①;②;③;④ , 其中正确的有( )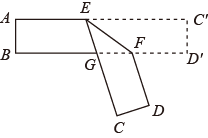 A、1个 B、2个 C、3个 D、4个7. 如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )
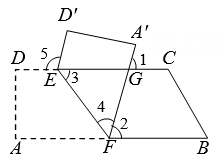
A、1个 B、2个 C、3个 D、4个7. 如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )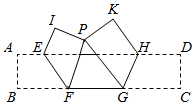 A、54° B、55° C、56° D、57°8. 如图,把四边形ABCD沿着EF折叠,给出下列条件:①∠1=∠2; ②∠3=∠4;③∠1+∠5=180°; ④∠1=∠4.能得出AB∥CD的个数为( )
A、54° B、55° C、56° D、57°8. 如图,把四边形ABCD沿着EF折叠,给出下列条件:①∠1=∠2; ②∠3=∠4;③∠1+∠5=180°; ④∠1=∠4.能得出AB∥CD的个数为( )
 A、1个 B、2个 C、3个 D、4个9. 如图,已知长方形纸片 ABCD,点E,F分别在边AD和BC上,且∠EFC=53°,H和G 分别是边AD和 BC 上的动点,现将点 A,B 沿 EF 向下折叠至点N,M 处,将点 C,D沿GH 向上折叠至点P,K 处,若 MN∥PK,则∠KHD的度数为 ( )
A、1个 B、2个 C、3个 D、4个9. 如图,已知长方形纸片 ABCD,点E,F分别在边AD和BC上,且∠EFC=53°,H和G 分别是边AD和 BC 上的动点,现将点 A,B 沿 EF 向下折叠至点N,M 处,将点 C,D沿GH 向上折叠至点P,K 处,若 MN∥PK,则∠KHD的度数为 ( )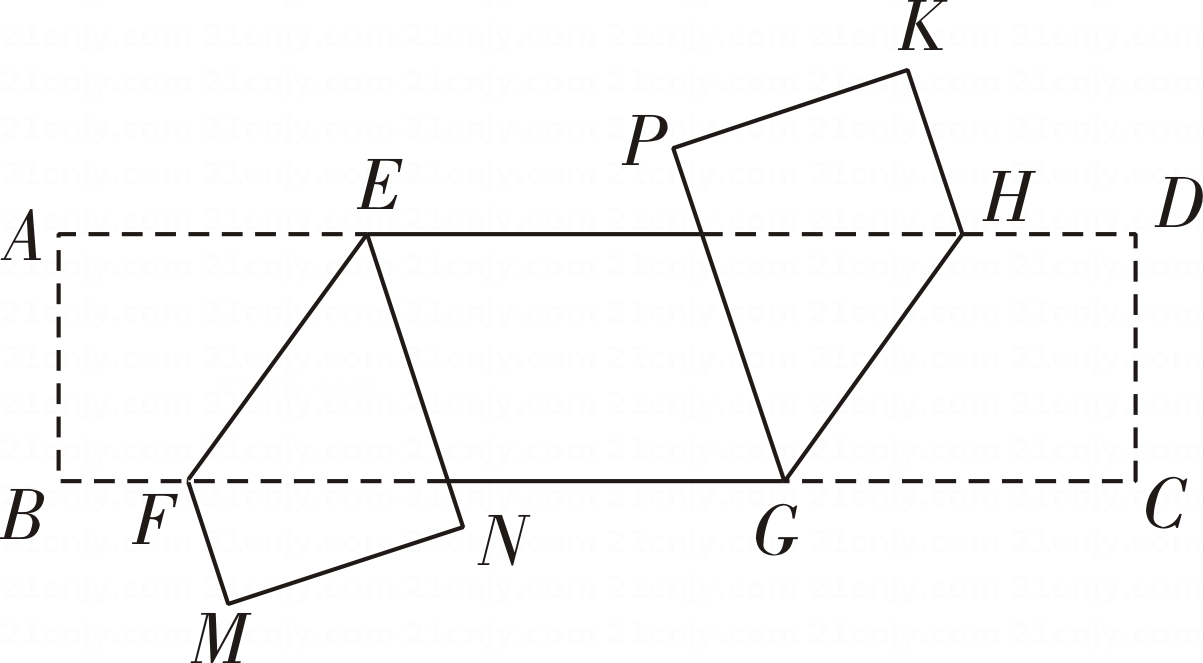 A、37°或143° B、74°或96° C、37°或105° D、74°或106°10. 如图,在中, , 按如图所示进行翻折,使 , , 则的度数是( )
A、37°或143° B、74°或96° C、37°或105° D、74°或106°10. 如图,在中, , 按如图所示进行翻折,使 , , 则的度数是( )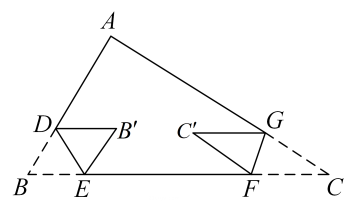 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
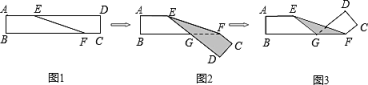
11. 如图1,点E、F是长方形纸带ABCD边上的两个点,∠DEF=20°,将这个纸带沿EF折叠成如图2的形状后,再沿BF折叠成图3的形状,则图3中的∠CFE的度数是度.
 12. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=49°,则∠2﹣∠1= .
12. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=49°,则∠2﹣∠1= .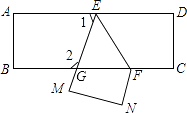 13. 如图是一款长臂折叠护眼灯示意图,与桌面垂直,当发光的灯管恰好与桌面平行时, , , 则的度数为°.
13. 如图是一款长臂折叠护眼灯示意图,与桌面垂直,当发光的灯管恰好与桌面平行时, , , 则的度数为°.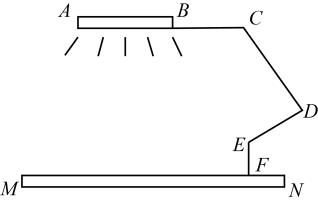 14. 如图,将一张三角形纸片的一角折叠,使得点落在四边形的外部的位置,且与点在直线的异侧,折痕为 , 已知 , 若保持的一边与平行,则的度数 .
14. 如图,将一张三角形纸片的一角折叠,使得点落在四边形的外部的位置,且与点在直线的异侧,折痕为 , 已知 , 若保持的一边与平行,则的度数 .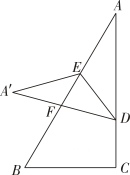 15. 如图1是我们常用的折叠式小刀,图2中刀柄外形是一个长方形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图2所示的∠1与∠2,若∠1=52°,则∠2的度数是 度.
15. 如图1是我们常用的折叠式小刀,图2中刀柄外形是一个长方形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图2所示的∠1与∠2,若∠1=52°,则∠2的度数是 度.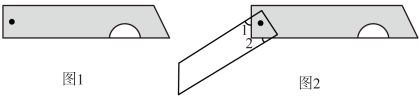 16. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB,CD.若CD∥BE,∠1=42°,则∠2的度数是 .
16. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB,CD.若CD∥BE,∠1=42°,则∠2的度数是 .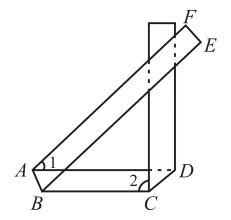 17. 如图,在长方形中,点、分别是线段、上的两点,点是线段上的一点,连结 , .将四边形沿着折叠,得到四边形.已知 , 若恰好平分 , 则的度数是 度.
17. 如图,在长方形中,点、分别是线段、上的两点,点是线段上的一点,连结 , .将四边形沿着折叠,得到四边形.已知 , 若恰好平分 , 则的度数是 度.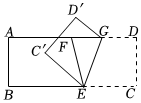 18. 如图,将长方形纸片沿折叠后,点 , 分别落在 , 的位置,再沿边将折叠到处,已知 , 则 ,
18. 如图,将长方形纸片沿折叠后,点 , 分别落在 , 的位置,再沿边将折叠到处,已知 , 则 ,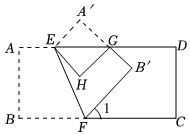
三、解答题
-
19. 如图1,有一张四边形ABCD纸片, ,点E,F分别在AD,BC上,把纸片沿EF折叠,点D,C分别与点G,H重合,FH交线段AD于点P.
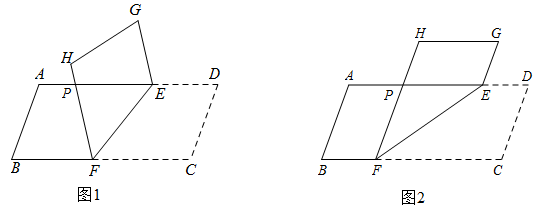 (1)、求证:∠GEA=∠HFB;(2)、如图2,∠D=70°,猜想当∠EFC多少度时, ,并说明理由.20. 如图1,将长方形纸片沿折叠得到图2,点 , 的对应点分别为点 , , 折叠后与相交于点.
(1)、求证:∠GEA=∠HFB;(2)、如图2,∠D=70°,猜想当∠EFC多少度时, ,并说明理由.20. 如图1,将长方形纸片沿折叠得到图2,点 , 的对应点分别为点 , , 折叠后与相交于点.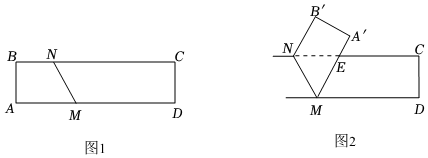 (1)、若 , 求的度数.(2)、设 , .
(1)、若 , 求的度数.(2)、设 , .①请用含的代数式表示.
②当恰好平分时,求的度数.
21. 如图,有一长方形纸带,E、F分别是边AD、BC上一点, 且 , 将纸带ABCD沿EF折叠成图1,再沿GF折叠成图2.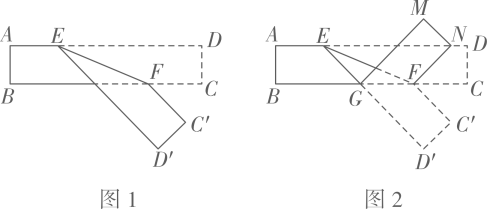
 (1)、当οα=25时,则∠FGD'= , ∠GFC'=;(2)、两次折叠后,求∠NFE的大小(用含α的代数式表示);(3)、当∠NFE和∠DEF的度数之和为100°时,求α的值.22. 有一条纸带ABCD,现小强对纸带进行了下列操作:
(1)、当οα=25时,则∠FGD'= , ∠GFC'=;(2)、两次折叠后,求∠NFE的大小(用含α的代数式表示);(3)、当∠NFE和∠DEF的度数之和为100°时,求α的值.22. 有一条纸带ABCD,现小强对纸带进行了下列操作: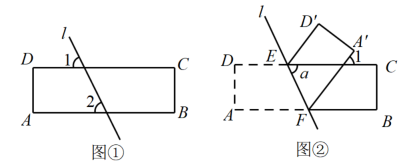 (1)、为了检验纸带的两条边线AB与CD是否平行,小强如图①所示画了直线后,量得∠1=∠2,则 , 理由为;(2)、将这条上下两边互相平行的纸带折叠,如图②所示,设∠1为70°,请求出∠的度数;(3)、如图③,已知这是一条长方形纸带,点E在折线AD→DC上运动,点F是AB上的动点,连接EF将纸带沿着EF折叠,使点A的对应点落在DC上,若 , 请用含x的代数式来表示的度数为.(直接写出答案)
(1)、为了检验纸带的两条边线AB与CD是否平行,小强如图①所示画了直线后,量得∠1=∠2,则 , 理由为;(2)、将这条上下两边互相平行的纸带折叠,如图②所示,设∠1为70°,请求出∠的度数;(3)、如图③,已知这是一条长方形纸带,点E在折线AD→DC上运动,点F是AB上的动点,连接EF将纸带沿着EF折叠,使点A的对应点落在DC上,若 , 请用含x的代数式来表示的度数为.(直接写出答案)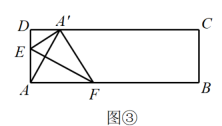 23. 如图①,将一张长方形纸片沿EF对折,使AB落在 的位置;
23. 如图①,将一张长方形纸片沿EF对折,使AB落在 的位置; (1)、若∠1的度数为a,试求∠2的度数(用含a的代数式表示);(2)、如图②,再将纸片沿GH对折,使得CD落在 的位置.
(1)、若∠1的度数为a,试求∠2的度数(用含a的代数式表示);(2)、如图②,再将纸片沿GH对折,使得CD落在 的位置.①若 ,∠1的度数为a,试求∠3的度数(用含a的代数式表示):
②若 ,∠3的度数比∠1的度数大20°,试计算∠1的度数.
24. 甲同学在学完《相交线与平行线》后,想通过折铁丝的方式进一步探索相交线与平行线的知识,他的具体操作步骤如下:第一步:将一根铁丝在 , , 处弯折得到如下图①的形状,其中 , .
第二步:将绕点D旋转一定角度,再将绕点E旋转一定角度并在上某点处弯折,得到如下图②的形状.
第三步:再拿出另外一根铁丝弯折成 , 跟前面弯折的铁丝叠放成如下图③的形状.
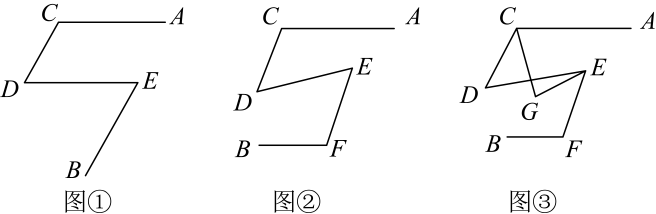
请根据上面的操作步骤,解答下列问题:
(1)、如图①,若 , 求;(2)、如图②,若 , 请判断 , , , 之间的数量关系,并说明理由;(3)、在(2)的条件下,如图③,若 , , 设 , , 求 . (用含 , 的式子表示)25. 图1是一个“有趣”的图形,它是由四个完全一样的直角三角形围成的一个大正方形ABCD,并且直角三角形的斜边又围成一个小正方形MNQP.已知每个直角三角形直角边分别是a,b(a<b),斜边为c.根据这个图形我们可以得到一些很好用的结论. (1)、如图1,设中间的小正方形MNQP面积为S1 , 请用两种方法来表示S1.(2)、如图2,将四个三角形向里面翻折,刚好又能形成一个更小的正方形A'B'C′D'.已知正方形A'B'C′D'的边长为3,正方形ABCD的边长为9.请求出a,b的值.(3)、连结B'D',若B'D′∥AD,请问∠DMN是多少度?请说明理由.
(1)、如图1,设中间的小正方形MNQP面积为S1 , 请用两种方法来表示S1.(2)、如图2,将四个三角形向里面翻折,刚好又能形成一个更小的正方形A'B'C′D'.已知正方形A'B'C′D'的边长为3,正方形ABCD的边长为9.请求出a,b的值.(3)、连结B'D',若B'D′∥AD,请问∠DMN是多少度?请说明理由.