2024年浙教版数学七(下)微素养核心突破3 平行线的判定与性质-三角板问题
试卷更新日期:2024-04-13 类型:复习试卷
一、选择题
-
1. 将一直角三角板与两边平行的纸条如图所示放置,若∠1=55°,则∠2的度数为( )
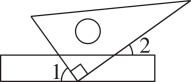 A、135° B、130° C、45° D、35°2. 一副分别含和的三角板如图所示摆放.若 , 则的度数是( )
A、135° B、130° C、45° D、35°2. 一副分别含和的三角板如图所示摆放.若 , 则的度数是( ) A、 B、 C、 D、3. 如图,直线 , 一块三角板的直角顶点在直线上,两直角边均与直线相交,若 , 则=( )
A、 B、 C、 D、3. 如图,直线 , 一块三角板的直角顶点在直线上,两直角边均与直线相交,若 , 则=( ) A、 B、 C、 D、4. 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=65°,则∠1的度数是( )
A、 B、 C、 D、4. 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=65°,则∠1的度数是( )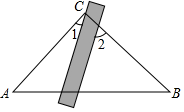 A、15° B、25° C、35° D、65°5. 直角三角板和直尺如图放置,若 , 则的度数为( )
A、15° B、25° C、35° D、65°5. 直角三角板和直尺如图放置,若 , 则的度数为( ) A、 B、 C、 D、6. 若将一副三角板按如图的方式放置,若 , 则的度数为( )
A、 B、 C、 D、6. 若将一副三角板按如图的方式放置,若 , 则的度数为( ) A、 B、 C、 D、7. 在同一平面内,将两个完全相同的三角板按如图摆放,可以画出两条互相平行的直线与 . 这样画的依据是( )
A、 B、 C、 D、7. 在同一平面内,将两个完全相同的三角板按如图摆放,可以画出两条互相平行的直线与 . 这样画的依据是( )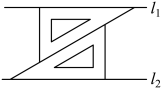 A、内错角相等,两直线平行 B、同位角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,内错角相等8. 一把直尺和一块含30°角的直角三角板ABC按如图方式摆放,直尺一边与三角板的两直角边分别交于点D和点E,另一边与三角板的两直角边分别交于点F和点A,且∠CED=35°,那么∠BAF的大小为( )
A、内错角相等,两直线平行 B、同位角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,内错角相等8. 一把直尺和一块含30°角的直角三角板ABC按如图方式摆放,直尺一边与三角板的两直角边分别交于点D和点E,另一边与三角板的两直角边分别交于点F和点A,且∠CED=35°,那么∠BAF的大小为( ) A、5° B、15° C、25° D、35°9. 如图l1∥l2点О在直线l1上,将三角板的直角顶点放在点О处,三角板的两条直角边与l2交于A,B两点,若∠1=35°,则∠2的度数为( )
A、5° B、15° C、25° D、35°9. 如图l1∥l2点О在直线l1上,将三角板的直角顶点放在点О处,三角板的两条直角边与l2交于A,B两点,若∠1=35°,则∠2的度数为( ) A、35° B、45° C、55° D、65°10. 将一副三角板如图放置,则下列结论中,正确的是( )
A、35° B、45° C、55° D、65°10. 将一副三角板如图放置,则下列结论中,正确的是( )①;②如果 , 则有;③如果 , 则有;④如果 , 则有 .
 A、①②③④ B、③④ C、①②④ D、①②③
A、①②③④ B、③④ C、①②④ D、①②③二、填空题
-
11. 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果 , 那么的度数为.
 12. 一直角三角板的直角顶点恰好放在直尺的边缘线上(如图所示),若 , 则度.
12. 一直角三角板的直角顶点恰好放在直尺的边缘线上(如图所示),若 , 则度. 13. 如图,把一块三角板的角的顶点放在直尺的一边上,若 , 则.
13. 如图,把一块三角板的角的顶点放在直尺的一边上,若 , 则.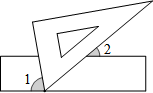 14. 如图所示,直线 ,三角板的直角顶点 落在直线 上,两条直角边分別交直线 于B,C两点.若 ,则 .
14. 如图所示,直线 ,三角板的直角顶点 落在直线 上,两条直角边分別交直线 于B,C两点.若 ,则 . 15. 将一把直尺和一块直角三角板如图放置,如果∠α=43°,则∠β的度数是度.
15. 将一把直尺和一块直角三角板如图放置,如果∠α=43°,则∠β的度数是度. 16. 将一副三角板按如图放置,则下列结论:①∠1=∠3;②如果∠2=30°,则有AC∥DE;③如果∠1=60°,则有BC∥AD④如果∠2=45°,必有∠4=∠C其中正确的有。
16. 将一副三角板按如图放置,则下列结论:①∠1=∠3;②如果∠2=30°,则有AC∥DE;③如果∠1=60°,则有BC∥AD④如果∠2=45°,必有∠4=∠C其中正确的有。
三、解答题
-
17. 如图1,直线与直线交于点O,().小明将一个含 , 的直角三角板如图1所示放置,使顶点P落在直线上,过点Q作直线交直线于点H(点H在Q左侧).
 (1)、若 , , 求的度数.(2)、如图2,若的角平分线交直线于点E.
(1)、若 , , 求的度数.(2)、如图2,若的角平分线交直线于点E.①当 , 时,求证:.
②小明将三角板保持并向左平移,运动过程中,探究与之间的数量关系,并说明理由.
18. 综合与实践问题情境:
数学课上,老师让同学们以“三角板与平行线”为主题开展数学活动.如图1,已知l1∥l2 , 直角三角板ABC中,∠B=90°,将其顶点A放在直线l2上,并使边AB⊥直线l1于点D,AC与l1相交于点H.老师提出问题:试判断边BC与直线l1的位置关系并说明理由.
 (1)、请解答老师提出的问题:(2)、如图2,将图1中三角板ABC的直角顶点B放在平行线之间,两直角边AB,CB分别与l1 , l2相交于点P,Q,得到∠1和∠2,试探究∠1与∠2的数量关系并说明理由.
(1)、请解答老师提出的问题:(2)、如图2,将图1中三角板ABC的直角顶点B放在平行线之间,两直角边AB,CB分别与l1 , l2相交于点P,Q,得到∠1和∠2,试探究∠1与∠2的数量关系并说明理由.
下面是小亮不完整的解答过程和解题反思,请你补充完整:
解:∠1+∠2=90°.过点B作直线BN∥l1 , 如图:
∵l1∥l2(已知)
∴BN∥l2( )
∴∠1= ▲ ∠2= ▲ ( )
∵∠ ▲ +∠ ▲ =∠ABC,∠ABC=90°
∴∠1+∠2=90°
解题反思:在图中“过点B作直线BN∥l1”的作用是 ▲
(3)、受小亮启发,同学们续探究下列问题.请从下列A,B两题中任选一题作答.我选择 ▲
A.在图2中作线段PO和QO,使它们分别平分∠1和∠2的对顶角,如图3.直接写出∠POQ的度数.
B.在图2中∠ABC内部作射线BE,过点B作射线BF⊥BE交直线L2于点M,得到∠3,如图4.直接写出∠1,∠3与∠EBC的数量关系.
19. 如图,直线 直线 ,一块三角板的顶点 在直线 上,边 、 分别交直线 于 、 两点. , , . (1)、如图1, ,则
(1)、如图1, ,则① ▲ °;
②若 与 的角平分线交于点 ,则 ▲ °.
(2)、如图2,点 在 的平分线上,连 ,且 ,若 ,求 的度数.(3)、如图3,若 , ,则 °(用含 的式子表示).20. 已知三角板中, , , , 长方形DEFG中, . 将三角板的顶点A放在长方形的边上,与相交于点M.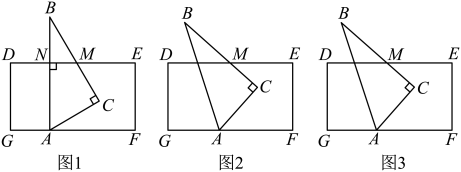 (1)、如图1,若 于点N,则的度数是 , 的度数是;(2)、如图2,请你猜想并写出与 的数量关系,并说明理由;(3)、请你总结(1),(2)的思路,在图3中探究与的数量关系?请直接写出数量关系.21. 将一副三角板中的两个直角顶点叠放在一起,其中 , ,
(1)、如图1,若 于点N,则的度数是 , 的度数是;(2)、如图2,请你猜想并写出与 的数量关系,并说明理由;(3)、请你总结(1),(2)的思路,在图3中探究与的数量关系?请直接写出数量关系.21. 将一副三角板中的两个直角顶点叠放在一起,其中 , ,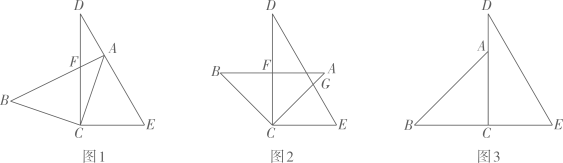 (1)、操作发现:如图1,当点落在线段上时,写出图中相等的角(写出三对即可);(2)、问题解决:如图2,若线段与交于点 .
(1)、操作发现:如图1,当点落在线段上时,写出图中相等的角(写出三对即可);(2)、问题解决:如图2,若线段与交于点 .①若时,求的度数;
②当为何值时,使线段最短;
(3)、深化拓展:如图3,将三角板绕点顺时针转动,直到边与重合即停止,转动的过程中当两块三角板恰有两边平行时,请直接写出的度数.22. 如图1,直线 , 直线与 , 分别交于点G,H, . 将一个直角三角板按如图1所示放置,使点N,M分别在直线 , 上,且在点G,H的右侧,已知 .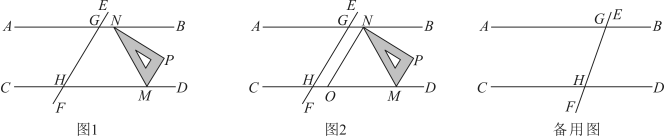 (1)、若 , 则的度数为;(2)、若 , 对说明理由;(3)、如图2,已知的平分线交直线于点O.
(1)、若 , 则的度数为;(2)、若 , 对说明理由;(3)、如图2,已知的平分线交直线于点O.①当 , 时,求的值;
②现将三角板保持 , 并沿直线向左平移,在平移的过程中,直接写出的度数(用含的代数式表示).
23. 题目:“如图1,已知内有一点P,射线 , 且与交于点E,过点P画射线平行于 , 与相交于点H.”嘉嘉用两个完全一样的三角板进行画图,画图过程如图2所示. (1)、嘉嘉的画图依据是;(2)、淇淇看了嘉嘉画出的图形后,对进行了如下说理.请你补全淇淇的说理过程;
(1)、嘉嘉的画图依据是;(2)、淇淇看了嘉嘉画出的图形后,对进行了如下说理.请你补全淇淇的说理过程;∵(已知),
∴ ▲ ( ).
∵(已知),
∴ ▲ ( ),
∴(等量代换);
(3)、小明看了(2)中淇淇的说理过程后,认为说法“若两个角的两边分别平行,则这两个角相等”正确,请你判断小明的说法是否正确,并说明理由.24. 问题情境我们知道“如果两条平行线被第三条直线所截,所截得的同位角相等,内错角相等,同旁内角互补”,所以在某些探究性问题中通过“构造平行线”可以起到转化角的作用.
已知三角板ABC中, , , , 长方形DEFG中, .
问题初探
如图(1),若将三角板ABC的顶点A放在长方形的边GF上,BC与DE相交于点M,于点N,则∠EMC的度数是多少呢?
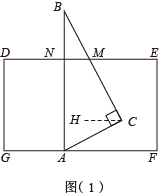
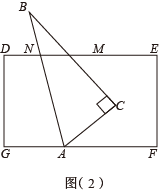
此题有多种解答方法,下面是小军同学的分析过程:
过点C作 , 则 , 这样就将∠CAF转化为∠HCA,∠EMC转化为∠MCH,从而可以求得∠EMC的度数.
(1)、请你直接写出 , ;(2)、 类比再探若将三角板ABC按图(2)所示方式摆放(AB与DE不垂直),请你猜想∠EMC与∠CAF的数量关系,并说明理由;
(3)、 方法迁移请你总结(1)(2)解决问题的思路,在图(2)中探究∠BAG与∠BMD的数量关系,并直接写出结果.
25. 综合与探究数学活动课上,老师以“一个含的直角三角板和两条平行线”为背景展开探究活动,

如图1,已知直线 , 直角三角板中, , .
(1)、如图1,若 , 则;(直接写出答案)(2)、“启航”小组在图1的基础上继续展开探究:如图 , 调整三角板的位置,当三角板的直角顶点在直线上,直线与 , 相交时,他们得出的结论是: , 你认为启航小组的结论是否正确,请说明理由;(3)、如图 , 受到“启航”小组的启发,“睿智”小组提出的问题是:在图的基础上,继续调整三角板的位置,当点不在直线上,直线与 , 相交时,与有怎样的数量关系?请你用平行线的知识说明理由.