2024年浙教版数学七(下)微素养核心突破2 平行线的相关模型
试卷更新日期:2024-04-13 类型:复习试卷
一、猪蹄模型
-
1. 如图,已知AB∥EF.若∠C=90°,则∠α,∠β,∠γ之间的关系是( )
 A、∠β=∠α+∠γ B、∠α+∠β+∠γ=180° C、∠α+∠β-∠γ=90° D、∠β+∠γ-∠α=90°2.
A、∠β=∠α+∠γ B、∠α+∠β+∠γ=180° C、∠α+∠β-∠γ=90° D、∠β+∠γ-∠α=90°2.如图,AB∥EF , 则∠A、∠C、∠D、∠E满足的数量关系是( )
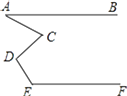 A、∠A+∠C+∠D+∠E=360° B、∠A+∠D=∠C+∠E C、∠A-∠C+∠D+∠E=180° D、∠E-∠C+∠D-∠A=90°3. 如图,若 , 用含有∠1,∠2,∠3的式子表示∠α,则∠α应为( )
A、∠A+∠C+∠D+∠E=360° B、∠A+∠D=∠C+∠E C、∠A-∠C+∠D+∠E=180° D、∠E-∠C+∠D-∠A=90°3. 如图,若 , 用含有∠1,∠2,∠3的式子表示∠α,则∠α应为( ) A、 B、 C、 D、4. ①如图1, , 则;②如图2, , 则;③如图3, , 则;④如图4, , 则 . 以上结论正确的个数是( )
A、 B、 C、 D、4. ①如图1, , 则;②如图2, , 则;③如图3, , 则;④如图4, , 则 . 以上结论正确的个数是( ) A、①②③④ B、①②③ C、②③④ D、①②④5.
A、①②③④ B、①②③ C、②③④ D、①②④5.如图,直线l1∥l2 , ∠α=∠β,∠1=50°,则∠2= .
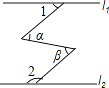 6. 如图,直线 , 则的度数为°.
6. 如图,直线 , 则的度数为°. 7. 如图,直线l1∥l2 , ∠BAE=125°,∠ABF=85°,则∠1+∠2= .
7. 如图,直线l1∥l2 , ∠BAE=125°,∠ABF=85°,则∠1+∠2= .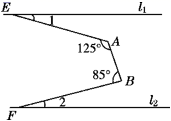 8. 某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论应用很广,请你利用这个结论解决以下问题:
8. 某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论应用很广,请你利用这个结论解决以下问题:已知直线 AB∥CD,点E在AB,CD 之间,点 P,Q分别在直线AB,CD上,连结 PE,EQ.
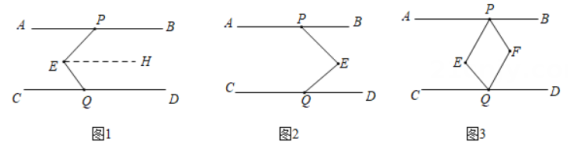 (1)、如图1,过点 E 作 EH∥AB,运用上述结论,探究∠PEQ,∠APE,∠CQE之间的数量关系,并说明理由.(2)、如图2,类比(1)中的方法,运用上述结论,探究∠PEQ,∠APE,∠CQE 之间的数量关系,并说明理由.(3)、如图3,PF 平分∠BPE,QF 平分∠EQD,当∠PEQ=140°时,请直接写出∠PFQ的度数.9. 如图
(1)、如图1,过点 E 作 EH∥AB,运用上述结论,探究∠PEQ,∠APE,∠CQE之间的数量关系,并说明理由.(2)、如图2,类比(1)中的方法,运用上述结论,探究∠PEQ,∠APE,∠CQE 之间的数量关系,并说明理由.(3)、如图3,PF 平分∠BPE,QF 平分∠EQD,当∠PEQ=140°时,请直接写出∠PFQ的度数.9. 如图 (1)、如图一, , , , 则 .(2)、如图二, , , , , 分别平分和 , 则 , 满足的数量关系为 .10. 阅读资料:在学习平行线知识的时候,小敏同学发现有的图形(如图1),不属于两条平行线被第三条直线所截的图形,不能直接应用平行线的性质解决问题.经过思考,小敏想到,若过点C作CF∥AB(如图2),这样就多了一个已知条件,问题就可以解决了.
(1)、如图一, , , , 则 .(2)、如图二, , , , , 分别平分和 , 则 , 满足的数量关系为 .10. 阅读资料:在学习平行线知识的时候,小敏同学发现有的图形(如图1),不属于两条平行线被第三条直线所截的图形,不能直接应用平行线的性质解决问题.经过思考,小敏想到,若过点C作CF∥AB(如图2),这样就多了一个已知条件,问题就可以解决了.
请你参考小敏同学的方法,解决下面问题:
(1)、如图2,已知AB∥DE,用等式表示∠B,∠E,∠BCE之间的数量关系,并说明理由.(2)、如图3,已知AB∥DE,直接用等式表示出∠B,∠E,∠BCE之间的数量关系.11. (1)、感知与探究:如图①,直线 , 过点作 . 请直接写出 , , 之间的数量关系:;(2)、应用与拓展:如图②,直线 . 若 , , , 借助第(1)问中的结论,求的度数;(3)、方法与实践:如图③,直线 . 若 , , 则 度.12. 同学们,观察小猪的猪蹄,你会发现一个熟悉的几何图形,我们就把这个图形的形象称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系.
(1)、感知与探究:如图①,直线 , 过点作 . 请直接写出 , , 之间的数量关系:;(2)、应用与拓展:如图②,直线 . 若 , , , 借助第(1)问中的结论,求的度数;(3)、方法与实践:如图③,直线 . 若 , , 则 度.12. 同学们,观察小猪的猪蹄,你会发现一个熟悉的几何图形,我们就把这个图形的形象称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系. (1)、如图1, , E为AB、CD之间一点,连接AE、CE.若∠A=42°,∠C=28°.则∠AEC= .(2)、如图2, , 线段AD与线段BC交于点E,∠A=36°,∠C=54°,EF平分∠BED,求∠BEF的度数.(3)、如图3. , 线段AD与线段BC相交于点G,∠BCD=56°,∠GDE=20°,过点D作交直线AB于点F,AE平分∠BAD,DG平分∠CDF,求∠AED的度数.13. 几何模型在解题中有着重要作用,例如美味的“猪蹄模型”.
(1)、如图1, , E为AB、CD之间一点,连接AE、CE.若∠A=42°,∠C=28°.则∠AEC= .(2)、如图2, , 线段AD与线段BC交于点E,∠A=36°,∠C=54°,EF平分∠BED,求∠BEF的度数.(3)、如图3. , 线段AD与线段BC相交于点G,∠BCD=56°,∠GDE=20°,过点D作交直线AB于点F,AE平分∠BAD,DG平分∠CDF,求∠AED的度数.13. 几何模型在解题中有着重要作用,例如美味的“猪蹄模型”.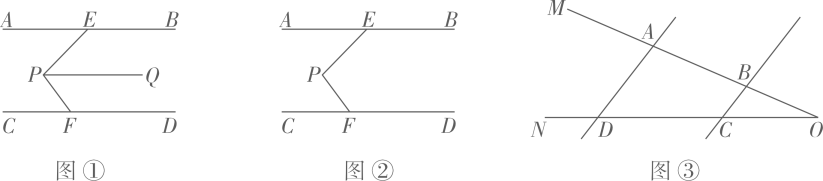 (1)、导入:如图①,已知 , 如果 , , 则;(2)、发现:如图②,直线 , 请判断与之间的数量关系,并说明理由;(3)、运用:如图③,已知在射线上运动(点与点三点不重合), , 请用含的代数式表示 , 并说明理由.14. 几何模型在解题中有着重要作用,例如美味的“猪蹄模型”.
(1)、导入:如图①,已知 , 如果 , , 则;(2)、发现:如图②,直线 , 请判断与之间的数量关系,并说明理由;(3)、运用:如图③,已知在射线上运动(点与点三点不重合), , 请用含的代数式表示 , 并说明理由.14. 几何模型在解题中有着重要作用,例如美味的“猪蹄模型”.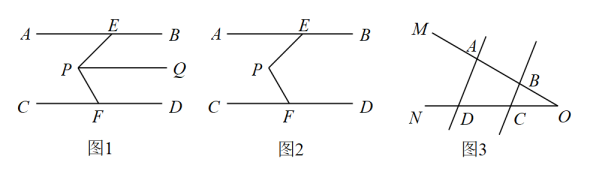 (1)、导入:如图1,已知 , 如果 , , 则;(2)、发现:如图2,直线 , 请判断与 , 之间的数量关系,并说明理由;(3)、运用:如图3,已知 , P在射线上运动(点P与点A、B、O三点不重合), , , 请用含、的代数式表示 , 并说明理由.15. 请阅读小明同学在学习平行线这章知识点时的一段笔记,然后解决问题.
(1)、导入:如图1,已知 , 如果 , , 则;(2)、发现:如图2,直线 , 请判断与 , 之间的数量关系,并说明理由;(3)、运用:如图3,已知 , P在射线上运动(点P与点A、B、O三点不重合), , , 请用含、的代数式表示 , 并说明理由.15. 请阅读小明同学在学习平行线这章知识点时的一段笔记,然后解决问题.小明:老师说在解决有关平行线的问题时,如果无法直接得到角的关系,就需要借助辅助线来帮助解答,今天老师介绍了一个“美味”的模型一“猪蹄模型”.即

已知:如图1, , 为 、 之间一点,连接 , 得到 .
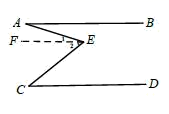
求证:
小明笔记上写出的证明过程如下:
证明:过点 作 ,
∴
∵ ,
∴
∴ .
∵
∴
请你利用“猪蹄模型”得到的结论或解题方法,完成下面的两个问题.
(1)、如图,若 , ,则 .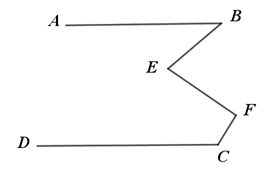 (2)、如图, , 平分 , 平分 , ,则 .
(2)、如图, , 平分 , 平分 , ,则 .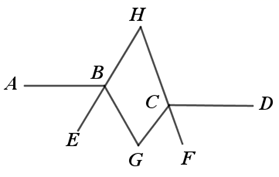 16. 如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
16. 如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1 ,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2 ,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3 , …,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En .
若∠En=1度,那∠BEC等于度
 17. 已知:直线AB与直线CD内部有一个点P , 连接BP .
17. 已知:直线AB与直线CD内部有一个点P , 连接BP . (1)、如图1,当点E在直线CD上,连接PE , 若∠B+∠PEC=∠P , 求证:AB∥CD;(2)、如图2,当点E在直线AB与直线CD的内部,点H在直线CD上,连接EH , 若∠ABP+∠PEH=∠P+∠EHD , 求证:AB∥CD;(3)、如图3,在(2)的条件下,BG、EF分别是∠ABP、∠PEH的角平分线,BG和EF相交于点G , EF和直线AB相交于点F , 当BP⊥PE时,若∠BFG=∠EHD+10°,∠BGE=36°,求∠EHD的度数.18. 探究题:已知:如图, , .求证:.
(1)、如图1,当点E在直线CD上,连接PE , 若∠B+∠PEC=∠P , 求证:AB∥CD;(2)、如图2,当点E在直线AB与直线CD的内部,点H在直线CD上,连接EH , 若∠ABP+∠PEH=∠P+∠EHD , 求证:AB∥CD;(3)、如图3,在(2)的条件下,BG、EF分别是∠ABP、∠PEH的角平分线,BG和EF相交于点G , EF和直线AB相交于点F , 当BP⊥PE时,若∠BFG=∠EHD+10°,∠BGE=36°,求∠EHD的度数.18. 探究题:已知:如图, , .求证:.
老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变形,继续做拓展探究,看看有什么新发现?
(1)、小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是 .(2)、接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线 , 然后在平行线间画了一点 , 连接后,用鼠标拖动点 , 分别得到了图 , 小颖发现图正是上面题目的原型,于是她由上题的结论猜想到图和图中的与之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.请你在小颖操作探究的基础上,继续完成下面的问题:
(ⅰ)猜想图中与之间的数量关系并加以证明;
(ⅱ)补全图 , 直接写出与之间的数量关系: ▲ .
二、铅笔头模型
-
19. 如图:已知 , 度, 度,则 等于( )度.
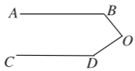 A、50 B、60 C、80 D、9020. 如图,已知A1B∥AnC,则∠A1+∠A2+…+∠An等于( )
A、50 B、60 C、80 D、9020. 如图,已知A1B∥AnC,则∠A1+∠A2+…+∠An等于( )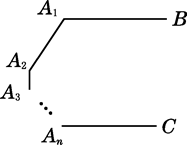 A、180°n B、(n+1)·180° C、(n-1)·180° D、(n-2)·180°21. 如图,已知 , 若按图中规律继续划分下去,则等于( )
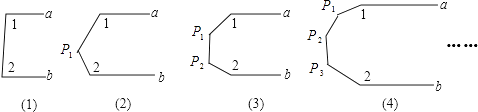
A、180°n B、(n+1)·180° C、(n-1)·180° D、(n-2)·180°21. 如图,已知 , 若按图中规律继续划分下去,则等于( ) A、 B、 C、 D、22.
A、 B、 C、 D、22.观察下列图形:已知a∥b,在第一个图中,可得∠1+∠2=180°,则按照以上规律,∠1+∠2+∠P1+…+∠Pn=度.
 23. 如图
23. 如图 (1)、[问题解决]如图1,AB∥CD,点E、F分别是AB、CD上的点,连接OE、OF,探求∠1、∠2、∠3之间的关系,并说明理由.(2)、[拓展延伸]如图2,上述结论还成立吗?如果成立,请证明;如果不成立,请写出它们的关系.(3)、 [拓展应用]如图3,已知AB∥CD,∠AE1E2的角平分线与∠CEnEn﹣1的角平分线交于点O.若∠E1OEn=m°直接写出∠2+∠3+∠4+…+∠(n﹣2)+∠(n﹣1)的度数.(用含m、n的代数式表示)
(1)、[问题解决]如图1,AB∥CD,点E、F分别是AB、CD上的点,连接OE、OF,探求∠1、∠2、∠3之间的关系,并说明理由.(2)、[拓展延伸]如图2,上述结论还成立吗?如果成立,请证明;如果不成立,请写出它们的关系.(3)、 [拓展应用]如图3,已知AB∥CD,∠AE1E2的角平分线与∠CEnEn﹣1的角平分线交于点O.若∠E1OEn=m°直接写出∠2+∠3+∠4+…+∠(n﹣2)+∠(n﹣1)的度数.(用含m、n的代数式表示)三、乌鸦嘴模型
-
24. 如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,则∠BCD的度数为.
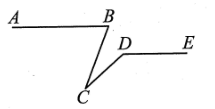 25. 如图, , 在的两边上分别过点A和点C向同方向作射线和 , 且 , 若和的角平分线所在的直线交于点P(P与C不重合),则的大小为 .
25. 如图, , 在的两边上分别过点A和点C向同方向作射线和 , 且 , 若和的角平分线所在的直线交于点P(P与C不重合),则的大小为 .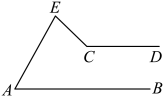 26. 如图, , 分别探讨下面四个图形中与、的关系,请你从(3)或(4)中任选一个加以说明.
26. 如图, , 分别探讨下面四个图形中与、的关系,请你从(3)或(4)中任选一个加以说明. 27.
27. (1)、【感知】如图1, , ∠AEP=50°,∠PFD=120°,求∠EPF的度数;(2)、【探究】如图2, , ∠AEP=48°,∠PFC=122°,求∠EPF的度数;(3)、【应用】如图3,在以上【探究】条件下,∠PEA的平分线和∠PFC的平分线交于点G,求∠G的度数.28. 小明完成作业后在家复习,他看到七下课本第12页例4,感到这个结论十分有趣,便尝试探究起来.
(1)、【感知】如图1, , ∠AEP=50°,∠PFD=120°,求∠EPF的度数;(2)、【探究】如图2, , ∠AEP=48°,∠PFC=122°,求∠EPF的度数;(3)、【应用】如图3,在以上【探究】条件下,∠PEA的平分线和∠PFC的平分线交于点G,求∠G的度数.28. 小明完成作业后在家复习,他看到七下课本第12页例4,感到这个结论十分有趣,便尝试探究起来. (1)、【基础巩固】
(1)、【基础巩固】与例4条件和结论互换,改成了:“如图1,AP 平分∠BAC,CP平分∠ACD,AB∥CD,则∠1+∠2=90°,”小明认为这个结论正确,你赞同他的想法吗? 请说明理由.
(2)、【尝试探究】小明发现:若将其中一条角平分线改成AC的垂线,则“∠1+∠2=90°”这个结论不成立.请帮小明完成探究:
如图2,AB∥CD,AP平分∠BAC,CP⊥AC,∠1是AP与AB的夹角,∠2 是CP与CD的夹角.
①若∠2=22°,求∠1的度数.
②试说明:2∠1-∠2=90°.
(3)、【拓展提高】如图3,若AB∥CD,AP⊥AC,CP平分∠ACD,请直接写出∠1与∠2的数量关系.