2024年浙教版数学七（下）微素养核心突破1 平行线的判定与性质-跨学科应用

试卷更新日期：2024-04-13 类型：复习试卷

进入出卷网下载

一、选择题

1. 光线在不同介质中的传播速度是不同的，因此当光线从水中射向空气时，要发生折射，由于折射率相同，所以在水中平行的光线，在空气中也是平行的．如图， $∠ 1 = 122 ° ， ∠ 2$ 的度数为（）

A、 $32 °$ B、 $58 °$ C、 $68 °$ D、 $78 °$

查看试题解析
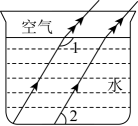2. 传统文化风筝是由中国古代劳动人民发明于东周春秋时期的产物，其材质在不断改进之后，坊间开始用纸做风筝，称为“纸鸢”．如图所示的纸骨架中，与 $∠ 3$ 构成同旁内角的是（　　）

A、 $∠ 1$ B、 $∠ 2$ C、 $∠ 4$ D、 $∠ 5$

查看试题解析
3. 太阳灶、卫星信号接收锅、探照灯及其他很多灯具都与抛物线有关．如图，从点 $O$ 照射到抛物线上的光线 $O B$ ， $O C$ 反射后沿着与 $P O$ 平行的方向射出，已知图中 $∠ A B O = 44 °$ ， $∠ B O C = 133 °$ ，则 $∠ O C D$ 的度数为（）

A、 $88 °$ B、 $89 °$ C、 $90 °$ D、 $91 °$

查看试题解析
4. 如图，一束平行于主光轴的光线经凸透镜折射后，其折射光线与一束经过光心 $O$ 的光线相交于点 $P$ ， $F$ 为焦点．若 $∠ 1 = 150 °$ ， $∠ 2 = 25 °$ ，则 $∠ 3$ 的度数为（）

A、 $40 °$ B、 $45 °$ C、 $50 °$ D、 $55 °$

查看试题解析
5. 为增强学生体质，感受中国的传统文化，学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间，小聪把它抽象成图2的数学问题：已知AB∥CD，∠EAB＝80°， $∠ E C D = 110 °$ ，则∠E的度数是（）

A、30° B、40° C、60° D、70°

查看试题解析
6. 如图，一束光线 $A B$ 先后经平面镜 $O M$ ， $O N$ 反射后，反射光线 $C D$ 与 $A B$ 平行，当 $∠ A B M = 35 °$ 时， $∠ D C N$ 的度数为（）

A、 $55 °$ B、 $70 °$ C、 $60 °$ D、 $35 °$

查看试题解析
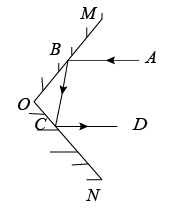7. 平面镜反射光的规律是：射到中面镜上的光线和被反射的光线与平面镜所夹的锐角相等，即如图①中∠α＝∠β；若如图②光线m被平面镜a和b两次反射后，反射出的光线n和入射光线m平行，且∠1＝40°，则∠2等于（）

A、40° B、80° C、90° D、100°

查看试题解析

二、填空题

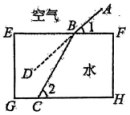8. 有经验的渔夫用鱼叉捕鱼时，不会将鱼叉对准他看到的鱼，这是由于光从空气射入水中时，发生折射现象.如图，水面 $E F$ 与底面 $G H$ 平行，光线 $A B$ 从空气射入水中时发生了折射，变成光线 $B C$ 射到水底 $C$ 处，射线 $B D$ 是光线 $A B$ 的延长线， $∠ 1 = 42 °$ ， $∠ 2 = 60 °$ ，则 $∠ C B D =$ $°$ .

查看试题解析
9. 光从一种介质射向另一种介质时会发生折射．如图，用直线 $m$ ， $n$ 表示一块玻璃的两个面，且 $m ∥ n$ ．现有一束光线 $A B$ 从空气射向玻璃， $B C$ 是折射光线， $D$ 为射线 $A B$ 延长线上一点．若 $∠ 1 = 20 °$ ， $∠ 2 = 145 °$ ，则 $∠ 3 =$ ．

查看试题解析
10. 如图1，当光线在空气进入水中时，会发生折射，满足入射角∠1与折射角∠2的度数比为4：3，如图2，在同一平面上，两条光线同时从空气进入水中，两条入射光线与水平面夹角度数分别为x ， y ，在水中两条折射光线的夹角度数为m、则m＝．（用含x ， y的式子表示）

查看试题解析
11. 如图，平面反光镜AC斜放在地面AB上，一束光线从地面上的P点射出，DE是反射光线.已知∠APD=120°，若要使反射光线DE∥AB，则∠CAB应调节为°(提示：∠ADP=∠CDE，三角形的内角和等于180°).

查看试题解析
12. 如图1，将支架平面镜 $A B$ 放置在水平桌面 $M N$ 上，激光笔 $P D$ 与水平天花板 $E F$ 的夹角（ $∠ E P G$ ）为 $30 °$ ，激光笔发出的入射光线 $D G$ 射到 $A B$ 上后，反射光线 $G H$ 与 $E F$ 形成 $∠ P H G$ ，由光的反射定律可知， $D G$ ， $G H$ 与 $A B$ 的垂线 $G K$ 所形成的夹角始终相等，即 $∠ 1 = ∠ 2$ ．

(1)、 $∠ G H F$ 的度数为；

(2)、如图2，点B固定不动，调节支架平面镜 $A B$ ，调节角为 $∠ A B M$ ．
①若 $∠ A B M = 30 °$ ，则 $∠ P H G$ 的度数为；

②若反射光线 $G H$ 恰好与 $E F$ 平行，则 $∠ A B M$ 的度数为．

查看试题解析

三、作图题

13. 台球运动中，如果母球P击中桌边点A，经桌边反弹击中相邻的另一桌边，再次反弹，那么母球P经过的路线BC与PA平行吗？请你把台球母球P的完整路线P-A-B-C画出来，并作出适当的标注或说明.

查看试题解析

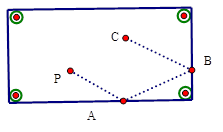
四、解答题

14. 已知，MN ， EF分别表示两面互相平行的平面镜，即 $M N ∥ E F$ ，一束光线AB照射到平面镜MN上，反射光线为BC ，此时 $∠ 1 = ∠ 2$ ；光线BC经平面镜EF反射后的反射光线为CD ，此时 $∠ 3 = ∠ 4$ .
求证： $A B ∥ C D$ .

查看试题解析
15. 如图， $M N$ ， $E F$ 分别表示两个互相平行的镜面，一束光线 $A B$ 照射到镜面 $M N$ 上，反射光线为 $B C$ ，此时 $∠ 1 = ∠ 2$ ；光线 $B C$ 经过镜面 $E F$ 反射后的光线为 $C D$ ，此时 $∠ 3 = ∠ 4$ ．试判断 $A B$ 与 $C D$ 的位置关系，并说明理由．
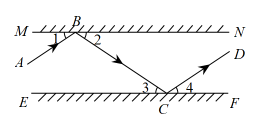
答： $A B ∥ C D$ ．
理由：延长射线 $B A$ 交 $E F$ 于点 $P$ ．
      $∵ M N ∥ E F$ ．
      $∴$ $∠ 2 =$     ▲  （  ）
      $∵$ $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ （已知）
      $∴$ $∠ 1 =$     ▲  （等量代换）
又 $∵$ $M N ∥ E F$ ，
      $∴$ $∠ 1 = ∠ B P C$ （  ）
      $∴$     ▲     （等量代换）
      $∴$ $A B ∥ C D$ （  ）

查看试题解析
16. 潜望镜是指从海面下伸出海面或从低洼坑道伸出地面，用以窥探海面或地面上活动的装置．其构造与普通地上望远镜相同，另加两个反射镜使从摄入潜望镜的光线经两次反射而折向眼中．潜望镜常用于潜水艇、坑道和坦克内用以观察敌情．如图，进入潜望镜的光线和离开潜望镜的光线是平行的，光线经过镜子反射时，∠1＝∠2，∠3＝∠4，请猜想潜望镜中两面镜子的位置关系，并说明理由．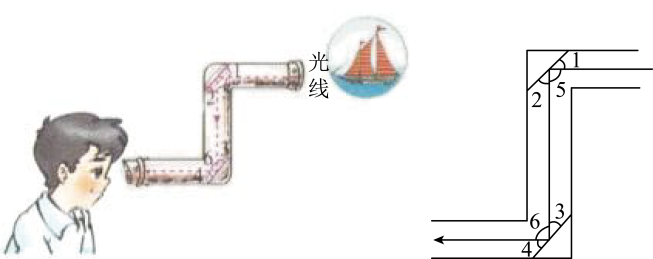

查看试题解析
17. 阅读下列材料，完成相应任务．
台球中的数学
如图1是台球桌面实物图，图2是抽象出的数学图形，已知长方形桌面 $A B C D$ 中， $A D ∥ B C$ ，一个球在桌面上的点 $E$ 处滚向桌边 $A D$ ，碰到 $A D$ 上的点 $F$ 后反弹，再碰到 $B C$ 边上的点 $G$ 后，再次反弹进入底袋点 $D$ ．在球碰到桌边反弹的过程中，击出线与桌边的夹角 $∠ 1$ 等于反弹线与桌边的夹角 $∠ 2$ ，同理 $∠ 3 = ∠ 4$ ．

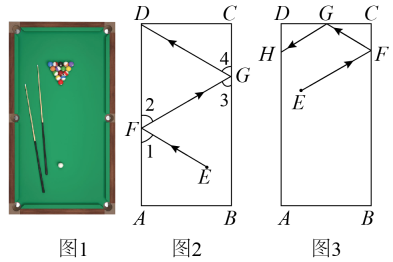(1)、任务一：如图2，求证： $E F ∥ G D$ ；

(2)、任务二：如图3，若球在桌面的点 $E$ 处，经过两次反弹后碰到 $A D$ 边上的点 $H$ 处，若 $∠ C F G + ∠ C G F = 90 °$ ，请你判断 $E F$ 与 $G H$ 的位置关系，并说明理由．

查看试题解析

五、实践探究题

18. 【学习新知】射到平面镜上的光线（入射光线）和反射后的光线（反射光线）与平面镜所夹的角相等．如图1，若入射光线与水平镜面夹角为 $∠ 1$ ，反射光线与水平镜面夹角为 $∠ 2$ ，则 $∠ 1 = ∠ 2$ ．

(1)、【初步应用】如图2，有两块平面镜 $A B$ ， $B C_{1}$ ，入射光线 $D O_{1}$ 经过两次反射，得到反射光线 $O_{2} E$ ，若 $∠ B = 90 °$ ，证明： $D O_{1} ∥ O_{2} E$ ；

(2)、【拓展探究】如图3，有三块平面镜 $A B$ ， $B C$ ， $C D$ ，入射光线 $E O_{1}$ 经过三次反射，得到反射光线 $O_{3} F$ ，已知 $∠ 1 = 36 °$ ， $∠ B = 120 °$ ，若要使 $E O_{1} ∥ O_{3} F$ ，则 $∠ C$ 为多少度？

查看试题解析

六、综合题

19. 阅读下列材料，并完成任务．
光线在不同介质中的传播速度是不同的，因此当光线从水中斜射向空气中时，要发生折射，由于折射率相同，所以在水中平行的光线，在空气中的折射光线也是平行的．如图，水面 $A B$ 与杯底 $C D$ 平行，光线 $E F$ 与 $H I$ 平行， $F G$ 与 $I J$ 平行．兴趣小组发现 $∠ E F G = ∠ H I J$ ．证明过程如下：

证明：∵ $E F ∥ H I$ ，
∴ $∠ E F B = ∠ H I B$ （依据），
∵ $F G ∥ I J$ ，
∴ $∠ G F B = ∠ J I B$ ，
∴ $∠ G F B + ∠ E F B = ∠ J I B + ∠ H I B$ ，
∴ $∠ E F G = ∠ H I J$ ．

(1)、任务一：上述材料中的“依据”指的是：；

(2)、任务二：若 $∠ F E D = 65 °$ ，求 $∠ F I H$ 的度数．

查看试题解析
20. 如图所示，把一根筷子一端放在水里，一端露出水面，筷子变弯了，它真的弯了吗？其实没有，这是光的折射现象，光从空气中射入水中，光的传播方向发生了改变．

(1)、请指出与∠1是同旁内角的有哪些角？请指出与∠2是内错角的有哪些角？

(2)、若∠1＝115°，测得∠BOM＝145°，从水面上看斜插入水中的筷子，水下部分向上折弯了多少度？请说明理由．

查看试题解析
21. 实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．如图，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b反射的光线为n．

(1)、当 $m ∥ n$ 时，若 $∠ 1 = 5 0^{∘}$ ，则∠2＝， ∠3＝；

(2)、当 $m ∥ n$ 时，若 $∠ 1 = x^{∘} (0 < x < 90)$ ，则∠3＝；

(3)、根据（1）（2）结果，反过来猜想：当两平面镜a，b的夹角∠3为多少度时， $m ∥ n$ ．请说明理由（可以在图中添加适当的角度标记进行说明）

查看试题解析
22. 如图1展示了光线反射定律：EF是镜面AB的垂线，一束光线m射到平面镜AB上，被AB反射后的光线为n，则入射光线m，反射光线n与垂线EF所夹的锐角θ₁＝θ₂ ．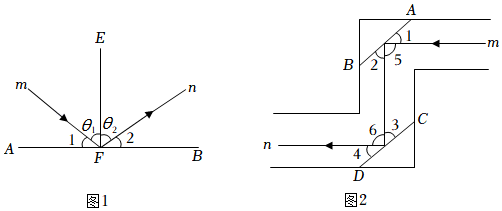

(1)、在图1中，证明：∠1＝∠2．

(2)、图2是潜望镜工作原理示意图，AB，CD是平行放置的两面平面镜．求证：m∥n．

查看试题解析
23. 【学科融合】
物理学中把经过入射点O并垂直于反射面的直线ON叫做法线，入射光线与法线的夹角i叫做入射角，反射光线与法线的夹角r叫做反射角（如图①）.由此可以归纳出如下的规律：

在反射现象中，反射光线、入射光线和法线都在同一平面内；反射光线、入射光线分别位于法线两侧；反射角等于入射角.这就是光的反射定律（rfectionlaw）.

【数学推理】如图1，有两块平面镜OM，ON，且OM⊥ON，入射光线AB经过两次反射，得到反射光线CD.由以上光的反射定律，可知入射角与反射角相等，进而可以推得他们的余角也相等，即：∠1＝∠2，∠3＝∠4.在这样的条件下，求证：AB∥CD.

【尝试探究】两块平面镜OM，ON，且∠MON＝α，入射光线AB经过两次反射，得到反射光线CD.

(1)、如图2，光线AB与CD相交于点E，则∠BEC＝；

(2)、如图3，光线AB与CD所在的直线相交于点E，CBED＝β，则α与β之间满足的等量关系是.

查看试题解析
24. 光线反射是一种常见的物理现象，在生活中有广泛地应用.例如提词器可以帮助演讲者在看演讲词的同时也能面对摄像机，自行车尾部的反光镜等就是应用了光的反射原理.

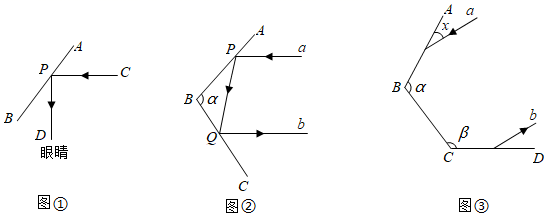(1)、提词器的原理如图①，AB表示平面镜，CP表示入射光线，PD表示反射光线，∠CPD＝90°，求∠APC的度数；

(2)、自行车尾部的反光镜在车灯照射下，能把光线按原来的方向返回（如图②），a表示入射光线，b表示反射光线，a∥b.平面镜AB与BC的夹角∠ABC＝ $α$ ，求 $α$ .

(3)、如图③，若 $α$ ＝108°，设平面镜CD与BC的夹角∠BCD＝ $β$ （90°＜ $β$ ＜180°），入射光线a与平面镜AB的夹角为x（0°＜x＜90°），已知入射光线a从平面镜AB开始反射，经过2或3次反射，当反射光线b与入射光线a平行时，请直接写出 $β$ 的度数.（可用含x的代数式表示）.

查看试题解析