2023-2024学年广东省八年级下学期期中仿真模拟卷三【人教版】
试卷更新日期:2024-04-13 类型:期中考试
一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,只有一个是正确的)
-
1. 下列各式中正确的是( )A、 B、 C、 D、2. 在下列以线段、、的长为三边的三角形中,不能构成直角三角形的是( )A、 , , B、 , , C、 D、 , ,3. 若 与最简二次根式 是同类二次根式,则m的值为( )A、7 B、11 C、2 D、14. 如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
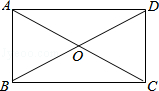 A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OB5. 如图,在平行四边形中,对角线 , 相交于点 , 点 , 分别是 , 的中点,连接 , 若 , 则的长为( )
A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OB5. 如图,在平行四边形中,对角线 , 相交于点 , 点 , 分别是 , 的中点,连接 , 若 , 则的长为( )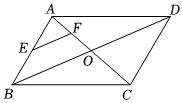 A、 B、 C、 D、6. 如图,在长方形中无重叠放入面积分别为和的两张正方形纸片,则图中空白部分的面积为( )
A、 B、 C、 D、6. 如图,在长方形中无重叠放入面积分别为和的两张正方形纸片,则图中空白部分的面积为( ) A、 B、 C、 D、7. 定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.已知在“等对角四边形”中, , , 则边的长是( )A、 B、 C、或 D、或8. 如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则AB+AD的值是( )
A、 B、 C、 D、7. 定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.已知在“等对角四边形”中, , , 则边的长是( )A、 B、 C、或 D、或8. 如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则AB+AD的值是( ) A、10 B、15 C、25 D、309. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.那么对于这个图中各部分的面积关系,说法不一定成立的是( )
A、10 B、15 C、25 D、309. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.那么对于这个图中各部分的面积关系,说法不一定成立的是( )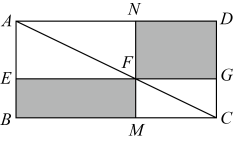 A、 B、 C、 D、10. 如图,已知正方形的边长为4,P是对角线上一点,于点E,于点F,连接 , . 给出下列结论:①;②四边形的周长为8;③一定是等腰三角形;④ . 其中正确结论的序号为( )
A、 B、 C、 D、10. 如图,已知正方形的边长为4,P是对角线上一点,于点E,于点F,连接 , . 给出下列结论:①;②四边形的周长为8;③一定是等腰三角形;④ . 其中正确结论的序号为( ) A、①②③④ B、①②④ C、②④ D、①②③
A、①②③④ B、①②④ C、②④ D、①②③二、填空题(本题有5小题,每小题3分,共15分)
-
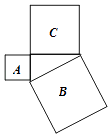
11. 已知则=。12. 如图,正方形A、B、C的边长分别为直角三角形的三边长,若正方形A、B的边长分别为3和5,则正方形C的面积为 .
 13. 如图,长为 , 宽为的矩形 , 阴影部分的面积为 .
13. 如图,长为 , 宽为的矩形 , 阴影部分的面积为 .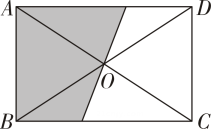 14. 如图,一个梯子斜靠在一竖直的墙上,测得 , 若梯子的顶端沿墙下滑 , 这时梯子的底端也向右滑 , 则梯子的长度为.
14. 如图,一个梯子斜靠在一竖直的墙上,测得 , 若梯子的顶端沿墙下滑 , 这时梯子的底端也向右滑 , 则梯子的长度为. 15. 如图平行四边形ABCD内有四个全等的正方形,他们都平行放置,每个正方形的左上角顶点B,E,F,G都在直线AB上,且BE=EF=FG,若直线PQ恰好经过点D,AB=14,CH=5,∠A=60°,则每个正方形的面积为.
15. 如图平行四边形ABCD内有四个全等的正方形,他们都平行放置,每个正方形的左上角顶点B,E,F,G都在直线AB上,且BE=EF=FG,若直线PQ恰好经过点D,AB=14,CH=5,∠A=60°,则每个正方形的面积为.
三、解答题(共8题,共75分)
-
16. 计算:(1)、(2)、17. 已知: , , 求:的值.18. 如图,E、F是平行四边形对角线上的两点,且.求证:四边形是平行四边形.
 19. 如图,某住宅小区在施工过程中留下了一块空地,已知米,米, , 米,米.
19. 如图,某住宅小区在施工过程中留下了一块空地,已知米,米, , 米,米. (1)、求这块空地的面积.(2)、若每种植1平方米草皮需要200元,问总共需投入多少元?20. 如图,在中, .
(1)、求这块空地的面积.(2)、若每种植1平方米草皮需要200元,问总共需投入多少元?20. 如图,在中, . (1)、用尺规作的平分线,交于点不写作法,保留作图痕迹;(2)、若 , , 求边上的高的长度.21. 问题:如图,在中, , , , 的平分线AE,BF分别与直线CD交于点E,F,求EF的长.
(1)、用尺规作的平分线,交于点不写作法,保留作图痕迹;(2)、若 , , 求边上的高的长度.21. 问题:如图,在中, , , , 的平分线AE,BF分别与直线CD交于点E,F,求EF的长.答案:.

探究:
(1)、把“问题”中的条件“”去掉,其余条件不变.①当点E与点F重合时,求AB的长;
②当点E与点C重合时,求EF的长.
(2)、把“问题”中的条件“ , ”去掉,其余条件不变,当点C,D,E,F相邻两点间的距离相等时,求的值.22. 如图,中,点是边上一个动点,过作直线设交的平分线于点 , 交的外角平分线于点 . (1)、求证:;(2)、若 , , 求的长;(3)、当点在边上运动到什么位置时,四边形是矩形?并说明理由.23. 综合与实践
(1)、求证:;(2)、若 , , 求的长;(3)、当点在边上运动到什么位置时,四边形是矩形?并说明理由.23. 综合与实践【课本再现】在一次课题学习活动中,老师提出了如下问题:如图1,四边形是正方形,点E是边的中点, , 且交正方形外角平分线于点F.请你探究与存在怎样的数量关系,并证明你的结论.
经过探究,小明得出的结论是 . 而要证明结论 , 就需要证明和所在的两个三角形全等,但和显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点E是边的中点,小明想到的方法是如图2,取的中点M,连接 , 证明 . 从而得到 .
 (1)、小明的证法中,证明≌的条件可以为( )A、边边边 B、边角边 C、角边角 D、斜边直角边(2)、【类比迁移】
(1)、小明的证法中,证明≌的条件可以为( )A、边边边 B、边角边 C、角边角 D、斜边直角边(2)、【类比迁移】
如图3,若把条件“点E是边的中点”改为“点E是边上的任意一点”,其余条件不变,是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.(3)、如图4,如果点E是边延长线上的任意一点,其他条件不变,是否仍然成立?(填“是”或“否”,不需证明);(4)、【拓展应用】
已知:四边形是正方形,点E是直线上的一点, , 且交正方形外角平分线于点F,若 , , 则的长为 .