2023-2024学年广东省八年级下学期期中仿真模拟卷二【北师大版范围:1-4章】
试卷更新日期:2024-04-13 类型:期中考试
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 做好“垃圾分类”,倡导绿色健康的生活方式,是我们做为公民应尽的义务,如图所示垃圾分类标志,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 等腰三角形中一个外角等于100°,则另两个内角的度数分别为( )A、40°,40° B、80°,20° C、50°,50° D、50°,50°或80°,20°3. 在下列现象中,属于平移的是( )A、小亮荡秋千运动 B、升降电梯由一楼升到八楼
2. 等腰三角形中一个外角等于100°,则另两个内角的度数分别为( )A、40°,40° B、80°,20° C、50°,50° D、50°,50°或80°,20°3. 在下列现象中,属于平移的是( )A、小亮荡秋千运动 B、升降电梯由一楼升到八楼
C、时针的运行过程 D、卫星绕地球运动4. 下列从左到右的变形中,属于因式分解的是( )A、 B、 C、 D、5. 若 , 则下列不等式成立的是( )A、a+5>b+5B、 C、 D、6. 若a-b=2,则a2-b2-4b的值是( )A、0 B、2 C、3 D、47. 如图,一次函数与一次函数的图象交于点 , 则关于的不等式的解集是( ) A、 B、 C、 D、8. 在△ABC中,AB=BC,两个完全相同的三角尺按如图所示的方式摆放,它们一组较短的直角边分别在AB,BC上,另一组较长的对应边的顶点重合于点P,BP交边AC于点D,下列结论中错误的是( ).
A、 B、 C、 D、8. 在△ABC中,AB=BC,两个完全相同的三角尺按如图所示的方式摆放,它们一组较短的直角边分别在AB,BC上,另一组较长的对应边的顶点重合于点P,BP交边AC于点D,下列结论中错误的是( ).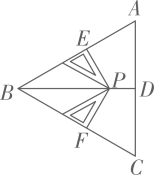 A、BP平分∠ABC B、AD=DC C、BD垂直平分AC D、AB= 2AD9. 如图,在中, , 分别以、为圆心,以大于的长为半径作弧,两弧分别交于、两点,连接直线 , 分别交、于点、 , 连接 , 则的面积为( )
A、BP平分∠ABC B、AD=DC C、BD垂直平分AC D、AB= 2AD9. 如图,在中, , 分别以、为圆心,以大于的长为半径作弧,两弧分别交于、两点,连接直线 , 分别交、于点、 , 连接 , 则的面积为( ) A、 B、 C、 D、10. 如图,C为线段AE上一动点(不与点A , E重合),在AE同侧分别作正三角形ABC和正三角形CDE , AD与BE交于点O , AD与BC交于点P , BE与CD交于点Q , 连接PQ . 以下四个结论:①AD=BE;②∠AOB=60°;③AP=BQ;④连接CO , 则AO=BO+CO . 恒成立的结论有( )
A、 B、 C、 D、10. 如图,C为线段AE上一动点(不与点A , E重合),在AE同侧分别作正三角形ABC和正三角形CDE , AD与BE交于点O , AD与BC交于点P , BE与CD交于点Q , 连接PQ . 以下四个结论:①AD=BE;②∠AOB=60°;③AP=BQ;④连接CO , 则AO=BO+CO . 恒成立的结论有( )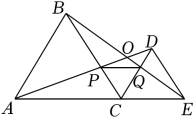 A、①②③ B、①② C、②③④ D、①②③④
A、①②③ B、①② C、②③④ D、①②③④二、填空题:本大题共5小题,每小题3分,共15分.
-
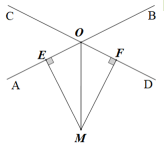
11. 点向右平移两个单位后得到的点和点关于轴对称,则 .12. 分解因式:2x3-8x=.13. 如图,直线AB,CD交于点O,ME⊥AB于点E,MF⊥CD于点F,若ME=MF,且∠AOC=52°,则∠OME的度数为.
 14. 定义新运算:对于任意实数a,b,都有 , 比如: . 若的值小于16,则满足条件的最小整数解为 .15. 如图,四边形ABCD中, , , , 连接 , 作角平分线交、于点F、E.若 , , 那么长为 .
14. 定义新运算:对于任意实数a,b,都有 , 比如: . 若的值小于16,则满足条件的最小整数解为 .15. 如图,四边形ABCD中, , , , 连接 , 作角平分线交、于点F、E.若 , , 那么长为 .
三、解答题(共8题,共75分)
-
16. 因式分解:(1)、(2)、17. 解不等式组 , 并把解集在数轴上表示出来.18. 【阅读】
定义:如果一个三角形有两个内角的差为90°,那么这样的三角形叫做“准直角三角形”.
(1)、【理解】①若 , , 则“准直角三角形”;(填“是”或“不是”)
②已知是“准直角三角形”,且 , , 则的度数为 .
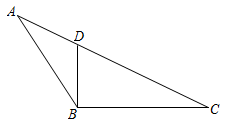
(2)、【应用】如图,在中,点D在上,连接 . 若 , , , , 试说明是“准直角三角形”.
 19. 某商店销售台型和台型电脑的利润为元,销售台型和台型电脑的利润为元.(1)、求每台型电脑和型电脑的销售利润各多少元;(2)、该商店计划一次购进两种型号的电脑共台,其中型电脑的进货量不超过型电脑的倍,设购进型电脑台,这台电脑的销售总利润为元.
19. 某商店销售台型和台型电脑的利润为元,销售台型和台型电脑的利润为元.(1)、求每台型电脑和型电脑的销售利润各多少元;(2)、该商店计划一次购进两种型号的电脑共台,其中型电脑的进货量不超过型电脑的倍,设购进型电脑台,这台电脑的销售总利润为元.①求关于的函数关系式;
②该商店购进型、型电脑各多少台,才能使销售总利润最大?
20. 阅读下面的“数学活动报告”,并完成相应学习任务.作的平分线活动内容:
已知 , 作出的平分线 .
方法展示:
方案一:如图①,分别在的边 , 上截取 , 再分别以点M,N为圆心,大于长为半径画弧,两弧相交于点C,则射线就是的平分线.
方案二:如图②,分别在的边 , 上用圆规截取 , 再利用三角尺分别过点 , 作出 , 的垂线,两条垂线交于点C,作射线 , 则就是的平分线.
方案三:如图③,在上取一点P,过点P作;然后在上截取 , 作射线 , 就是的平分线.
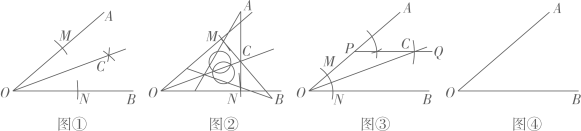
活动总结:
全等三角形、等腰三角形的性质是证明两角相等的重要依据,根据全等三角形、等腰三角形的有关知识可以用多种方法作的平分线.
活动反思:
利用等腰三角形“三线合一”的性质可以作出的平分线吗?
学习任务:
(1)、方案一依据的一个基本事实是;方案二“判定直角三角形全等”的依据是;(2)、同学们提出的方案三是否符合题意?请你利用图③说明理由;(3)、请依据等腰三角形“三线合一”的性质,在图④中作出的平分线,并简要叙述作图过程.21. 有些多项式的某些项可以通过适当地结合,(或把某项适当地拆分)成为一组,利用分组来分解多项式的因式,从而达到因式分解的目的,例如将因式分解。原式。
请在这种方法的启发下,解决以下问题:
(1)、分解因式;(2)、三边 , , 满足 , 判断的形状,并说明理由。(3)、“赵爽弦图”是由四个全等的直角三角形围成的一个大正方形,中间是一个小正方形。若直角三角形的两条直角边长分别是和 , 斜边长是4,小正方形的面积是1。根据以上信息,先将因式分解,再求值。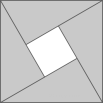 22. 为更好地推进生活垃圾分类工作,改善城市生态环境,某小区准备购买、两种型号的垃圾箱,通过对市场调研得知:购买3个型垃圾箱和2个型垃圾箱共需390元,购买2个型垃圾箱比购买1个型垃圾箱少用20元.(1)、求每个型垃圾箱和每个型垃圾箱分别多少元?(2)、该小区计划用不多于1500元的资金购买、两种型号的垃圾箱共20个,且型号垃圾箱个数不多于型垃圾箱个数的3倍,则该小区购买、两种型号垃圾箱的方案有哪些?该小区最少需花费多少钱?23. 数学模型学习与应用:
22. 为更好地推进生活垃圾分类工作,改善城市生态环境,某小区准备购买、两种型号的垃圾箱,通过对市场调研得知:购买3个型垃圾箱和2个型垃圾箱共需390元,购买2个型垃圾箱比购买1个型垃圾箱少用20元.(1)、求每个型垃圾箱和每个型垃圾箱分别多少元?(2)、该小区计划用不多于1500元的资金购买、两种型号的垃圾箱共20个,且型号垃圾箱个数不多于型垃圾箱个数的3倍,则该小区购买、两种型号垃圾箱的方案有哪些?该小区最少需花费多少钱?23. 数学模型学习与应用:白日登山望峰火,黄昏饮马傍交河.——《古从军行》唐李欣
模型学习:诗中隐含着一个有趣的数学问题,我们称之为“将军饮马”问题.关键是利用轴对称变换,把直线同侧两点的折线问题转化为直线两侧的线段问题,从而解决距离和最短的一类问题,“将军饮马”问题的数学模型如图1所示:在直线l上存在点P , 使PA+PB的值最小.
作法:作A点关于直线l的对称点A',连接A'B , A'B与直线l的交点即为点P . 此时PA+PB的值最小.
 (1)、模型应用:
(1)、模型应用:如图2,已知△ABC为等边三角形,高AH=8cm , P为AH上一动点,D为AB的中点.
①当PD+PB的最小值时,在图中确定点P的位置(要有必要的画图痕迹,不用写画法).
②则PD+PB的最小值为 ▲ cm .
(2)、模型变式:如图3所示,某地有块三角形空地AOB , 已知∠AOB=30°,P是△AOB内一点,连接PO后测得PO=10米,现当地政府欲在三角形空地AOB中修一个三角形花坛PQR , 点Q、R分别是OA , OB边上的任意一点(不与各边顶点重合),求△PQR周长的最小值.