2023-2024学年广东省八年级下学期期中仿真模拟卷一【北师大版范围:1-3章】
试卷更新日期:2024-04-13 类型:期中考试
一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,只有一个是正确的)
-
1. 下列环保标志图案既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若成立,则下列不等式成立的是( )A、 B、 C、 D、3. 下列现象中,不属于平移的是( )A、滑雪运动员在平坦的雪地上沿直线滑行 B、时针的走动 C、商场自动扶梯上顾客的升降运动 D、火车在笔直的铁轨上行驶4. 一个等腰三角形的周长为13cm,一边长为5cm,则另两边长分别为( )A、3cm,5cm B、4cm,4cm C、3cm,5cm或4cm,4cm D、以上都不对5. 若不等式组的解集是 , 则的取值范围是( )A、 B、 C、 D、6. 如图,直线与直线交于点 , 则关于x的不等式的解集为( )
2. 若成立,则下列不等式成立的是( )A、 B、 C、 D、3. 下列现象中,不属于平移的是( )A、滑雪运动员在平坦的雪地上沿直线滑行 B、时针的走动 C、商场自动扶梯上顾客的升降运动 D、火车在笔直的铁轨上行驶4. 一个等腰三角形的周长为13cm,一边长为5cm,则另两边长分别为( )A、3cm,5cm B、4cm,4cm C、3cm,5cm或4cm,4cm D、以上都不对5. 若不等式组的解集是 , 则的取值范围是( )A、 B、 C、 D、6. 如图,直线与直线交于点 , 则关于x的不等式的解集为( )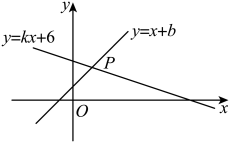 A、 B、 C、 D、7. 如图, , 将直角三角形沿着射线方向平移 , 得三角形已知 , 则阴影部分的周长为( )
A、 B、 C、 D、7. 如图, , 将直角三角形沿着射线方向平移 , 得三角形已知 , 则阴影部分的周长为( ) A、 B、 C、 D、8. 下列说法,错误的是( )A、一个三角形两边的垂直平分线的交点到这个三角形三个顶点的距离相等 B、“若 , 则”的逆命题是假命题 C、在角的内部到角的两边距离相等的点一定在这个角的平分线上 D、用反证法证明“三角形中必有一个角不大于”,先假设这个三角形中有一个内角大于60°9. 如图,中, , , 点B的坐标为 , 将绕点A逆时针旋转得到 , 当点O的对应点C落在上时,点D的坐标为( )
A、 B、 C、 D、8. 下列说法,错误的是( )A、一个三角形两边的垂直平分线的交点到这个三角形三个顶点的距离相等 B、“若 , 则”的逆命题是假命题 C、在角的内部到角的两边距离相等的点一定在这个角的平分线上 D、用反证法证明“三角形中必有一个角不大于”,先假设这个三角形中有一个内角大于60°9. 如图,中, , , 点B的坐标为 , 将绕点A逆时针旋转得到 , 当点O的对应点C落在上时,点D的坐标为( )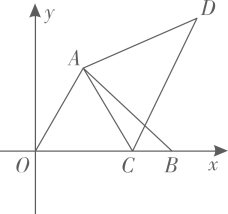 A、 B、 C、 D、10. 如图, 中, 分别是 上的点,作 ,垂足分别是 若 , 下面三个结论:① ② ③ 其中正确的是( )
A、 B、 C、 D、10. 如图, 中, 分别是 上的点,作 ,垂足分别是 若 , 下面三个结论:① ② ③ 其中正确的是( )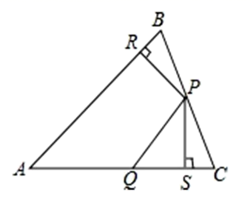 A、①③ B、②③ C、①② D、①②③
A、①③ B、②③ C、①② D、①②③二、填空题(本题有5小题,每小题3分,共15分)
-
11. 某棵树在栽种时树围是5cm,在一定生长期内每年增加约3cm,设经过年后这棵树的树围超过23cm,请列出满足的关系式 .12. 已知点B的坐标为(-5,1),它向右平移4个单位长度,再向上平移2个单位长度,得到点B′,则点B′的坐标为 .13. 如图,点P是平分线上一点, , 垂足为D,且 , 点M是射线上一动点,则的最小值为 .
 14. 若整数使得关于的方程的解为非负数,且使得关于的一元一次不等式组至少有个整数解,则所有符合条件的整数的和为 .15. 如图,已知菱形的边长为 , , 为的中点,若为对角线上一动点,则的最小值为.
14. 若整数使得关于的方程的解为非负数,且使得关于的一元一次不等式组至少有个整数解,则所有符合条件的整数的和为 .15. 如图,已知菱形的边长为 , , 为的中点,若为对角线上一动点,则的最小值为.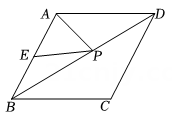
三、解答题(共8题,共75分)
-
16. 解不等式组 , 并把解集在数轴上表示出来.
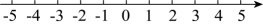 17. 甲、乙两家旅行社为了吸引更多的顾客,分别推出赴某地旅游的团体(多于4人)优惠办法.甲旅行社的优惠办法是:买4张全票,其余人按半价优惠;乙旅行社的优惠办法是:所有人都打七五折优惠.已知这两家旅行社的原价均为每人1000元,那么随着团体人数的变化,哪家旅行社的收费更优惠.18. 如图,中,平分 , 的中垂线交于点 , 交于点 , 连接 . 若 , , 求的度数.
17. 甲、乙两家旅行社为了吸引更多的顾客,分别推出赴某地旅游的团体(多于4人)优惠办法.甲旅行社的优惠办法是:买4张全票,其余人按半价优惠;乙旅行社的优惠办法是:所有人都打七五折优惠.已知这两家旅行社的原价均为每人1000元,那么随着团体人数的变化,哪家旅行社的收费更优惠.18. 如图,中,平分 , 的中垂线交于点 , 交于点 , 连接 . 若 , , 求的度数.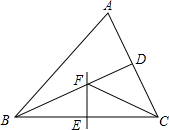 19. 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的顶点均在格点上.
19. 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的顶点均在格点上.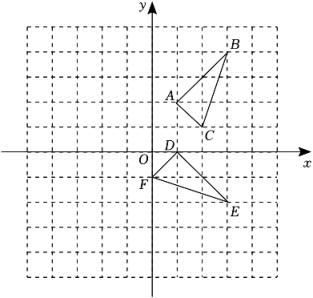 (1)、画出将△ABC关于原点O的中心对称图形△A1B1C1;(2)、将△DEF绕点E逆时针旋转90°得到△D1EF1 , 画出△D1EF1;(3)、若△DEF由△ABC绕着某点旋转得到的,则这点的坐标为 .20. 已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q.
(1)、画出将△ABC关于原点O的中心对称图形△A1B1C1;(2)、将△DEF绕点E逆时针旋转90°得到△D1EF1 , 画出△D1EF1;(3)、若△DEF由△ABC绕着某点旋转得到的,则这点的坐标为 .20. 已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q.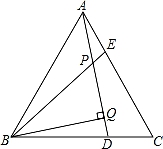 (1)、求证:BE=AD;(2)、求∠BPQ的度数;(3)、若PQ=3,PE=1,求AD的长.21. 如图,交延长线于 , 于 , , .
(1)、求证:BE=AD;(2)、求∠BPQ的度数;(3)、若PQ=3,PE=1,求AD的长.21. 如图,交延长线于 , 于 , , .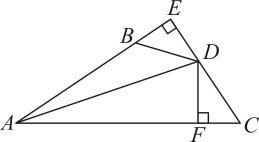 (1)、求证:平分;(2)、直接写出与之间的数量关系.22. 为了响应习主席提出的“足球进校园”的号召,某中学开设了“足球大课间活动”,该中学购买A种品牌的足球30个,B种品牌的足球20个,共花费3100元,已知B种品牌足球的单价比A种品牌足球的单价高30元.(1)、求A、B两种品牌足球的单价各多少元?(2)、根据需要,学校决定再次购进A、B两种品牌的足球50个,正逢体育用品商店“优惠促销“活动,A种品牌的足球单价优惠4元,B种品牌的足球单价打8折,如果此次学校的买A,B两种品牌足球的总费用不超过2750元,且购买B种品牌的足球不少于24个,
(1)、求证:平分;(2)、直接写出与之间的数量关系.22. 为了响应习主席提出的“足球进校园”的号召,某中学开设了“足球大课间活动”,该中学购买A种品牌的足球30个,B种品牌的足球20个,共花费3100元,已知B种品牌足球的单价比A种品牌足球的单价高30元.(1)、求A、B两种品牌足球的单价各多少元?(2)、根据需要,学校决定再次购进A、B两种品牌的足球50个,正逢体育用品商店“优惠促销“活动,A种品牌的足球单价优惠4元,B种品牌的足球单价打8折,如果此次学校的买A,B两种品牌足球的总费用不超过2750元,且购买B种品牌的足球不少于24个,
①若购买A品牌的m个,则购买B品牌 ▲ 个;②有几种购买方案?为了节约资金,学校应选择哪种方案?23. 数学课上,刘老师出示了如下的题目:如图1,在等边中,点在上,点在的延长线上,且 , 试确定线段与的大小关系,并说明理由.
小敏与同桌小聪探究解答的思路如下:
(1)、特殊情况,探索结论:当点为的中点时,如图2,确定线段与的大小关系,请你直接写出结论:(填“>”或填“<”或填“=”)
(2)、特例启发,解答题目:解:题目中,与的大小关系是: (填“>”或填“<”或填“=”).
理由如下:如图3,过点作 , 交于点.(请你补充完成解答过程)
(3)、拓展结论,设计新题:小敏解答后,提出了新的问题:在等边中,点在直线上,点在直线上,且 , 已知的边长为3, , 则的长=(请直接写出结果,备用图供选用).