2023-2024学年广东省深圳市八年级下学期数学期中仿真模拟卷二【范围：1-3章】

试卷更新日期：2024-04-13 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分，每小题有四个选项，只有一个是正确的）

1. 下列与杭州亚运会有关的图案中，中心对称图形是（）

A、 B、 C、 D、

查看试题解析
2. 交通法规人人遵守，文明城市处处安全．在通过桥洞时，我们往往会看到下图所示的标志，这是限制车高的标志，则通过该桥洞的车高 $x (m)$ 的范围可表示为（）

A、 $x \geq 4.5$ B、 $x > 4.5$ C、 $x \leq 4.5$ D、 $0 < x \leq 4.5$

查看试题解析
3. 若 $a > b$ ，那么下列各式中正确的是（）

A、 $a - 2 < b - 2$ B、 $- a > - b$ C、 $- 2 a < - 2 b$ D、 $\frac{a}{2} < \frac{b}{2}$

查看试题解析
4. 如图，△ABC是等边三角形，点D在AC边上，∠DBC＝40°，则∠ADB的度数为（）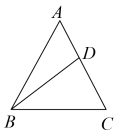

A、25° B、60° C、90° D、100°

查看试题解析
5. 如图所示，在 $△ A B C$ 中， $A B = A C$ ， $A D$ 是 $△ A B C$ 的角平分线. $D E ⊥ A B$ ， $D F ⊥ A C$ ，垂足分别为E、F，下列选项中错误的是（）

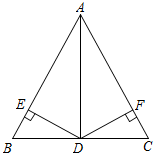A、 $B D = C D$ 且 $A D ⊥ B C$ B、 $D E = D F$ C、 $∠ B D E = ∠ C D F$ D、若点P为 $A C$ 上任意一点，且 $D E = 3$ ，则 $D P$ 的取值范围是 $P D < 3$

查看试题解析
6. 用 $(- 2 ， 4)$ 表示一只蚂蚁的位置，若这只蚂蚁先水平向右爬行3个单位，然后又竖直向下爬行2个单位，（）

A、 $(1 ， 6)$ B、 $(- 5，2)$ C、 $(1 ， 2)$ D、 $(2 ， 1)$

查看试题解析
7. 下列命题的逆命题是真命题的是（）

A、对顶角相等 B、有两边相等的三角形是等腰三角形 C、等边三角形是锐角三角形 D、全等三角形的对应角相等

查看试题解析
8. 如图，直线 $y = x + b$ 和 $y = k x + 2$ 与x轴分别交于点 $A (- 2 ， 0)$ ，点 $B (3 ， 0)$ ，则 ${\begin{array}{l} x + b > 0 \\ k x + 2 > 0 \end{array}$ 解集为（）

A、 $x < - 2$ B、 $x > 3$ C、 $x < - 2$ 或 $x > 3$ D、 $- 2 < x < 3$

查看试题解析
9. 把一些书分给同学，设每个同学分x本．若____；若分给11个同学，则书有剩余．可列不等式8（x+6）＞11x ，则横线的信息可以是（　　）

A、分给8个同学，则剩余6本 B、分给6个同学，则剩余8本 C、如果分给8个同学，则每人可多分6本 D、如果分给6个同学，则每人可多分8本

查看试题解析
10. 如图， $B D$ 为 $△ A B C$ 的角平分线，且 $B D = B C$ ， $E$ 为 $B D$ 延长线上的一点， $B E = B A$ ，过 $E$ 作 $E F ⊥ A B$ ， $F$ 为垂足．下列结论：① $△ A B D ≌ △ E B C$ ；② $∠ B C E + ∠ B C D = 180 °$ ；③ $A D = A E = E C$ ；④ $B A + B C = 2 B F$ ．其中正确的是（）

A、①②③ B、①③④ C、①②④ D、①②③④

查看试题解析

二、填空题（本题有5小题，每小题3分，共15分）

11. 如图，在 $△ A B C$ 中， $A B = A C$ ， $D$ 是 $B C$ 边上的中点，若 $A B = 13$ ， $A D = 12$ ，则 $B C$ 的长为．

查看试题解析
12. 小雨是小学一年级的小朋友，在认识直角三角形的学习活动中，需要完成一个剪直角三角形的剪纸活动，上初二的姐姐知知刚学完勾股定理的相关知识，她对妺妺说，我不用直角三角尺或量角器也可以判断你剪的卡片是否为直角三角形．知知量出两个三角形的三边长分别为：图形① $9 c m$ ， $12 c m$ ， $15 c m$ ；图形② $10 c m$ ， $10 c m$ ， $15 c m$ ．请你用所学知识判断：图形是直角三角形．

查看试题解析
13. 如图，在△ABC中，∠C =45°，AB的垂直平分线交AB于点E ，交BC于点D；AC的垂直平分线交AC于点G ，交BC于点F ，连接 AD ， AF ．若AF=2cm，BC=8cm，则DF=cm．

查看试题解析
14. 如图，将线段 $A B$ 平移到线段 $C D$ 的位置，则 $a + b$ 的值为．

查看试题解析
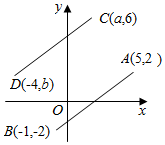15. 如图，已知等腰△ABC，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，下面结论：①∠APO=∠ACO；②∠APO+∠PCB=90°；③PC=PO；④AO+AP=AC；其中正确的有.(填上所有正确结论的序号)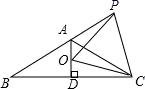

查看试题解析

三、解答题（共7题，共55分）

16. 解不等式组： ${\begin{matrix} x - 5 \leq 3 (x - 1) \\ \frac{x + 3}{2} > 2 x \end{matrix}$ ，并写出它的所有整数解．

查看试题解析

17. 某公司为了开发新产品，用A、B两种原料各360千克、290千克，试制甲、乙两种新型产品共50件，下表是试验每件新产品所需原料的相关数据：

原料

含量
产品

(单位：千克)

B
(单位：千克)

甲

乙

(1)、设生产甲种产品x件，根据题意列出不等式组，求出x的取值范围；

(2)、若甲种产品每件成本为70元，乙种产品每件成本为90元，设两种产品的成本总额为y元，求出成本总额y（元）与甲种产品件数x（件）之间的函数关系式；当甲、乙两种产品各生产多少件时，产品的成本总额最少？并求出最少的成本总额．

查看试题解析

18. 如图，平面直角坐标系内，小正方形网格的边长为 $1$ 个单位长度， $△ A B C$ 的三个顶点的坐标分别为 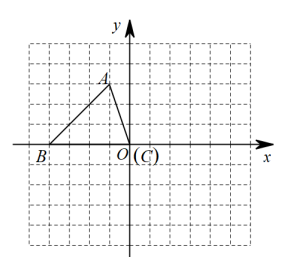$A (- 1 ， 3)$ ， $B (- 4 ， 0)$ ， $C (0 ， 0)$ ．

(1)、将 $△ A B C$ 向上平移 $1$ 个单位长度，再向右平移 $5$ 个单位长度后得到的 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ，并直接写出点 $A_{1}$ 的坐标；

(2)、 $△ A B C$ 绕原点O逆时针方向旋转 $90 °$ 得到 $△ A_{2} B_{2} O$ ，按要求作出图形；

(3)、如果 $△ A_{2} B_{2} O$ ，通过旋转可以得到 $△ A_{1} B_{1} C_{1}$ ，请直接写出旋转中心P的坐标．

查看试题解析
19. 如图，点O是等边 $△$ ABC内一点，将CO绕点C顺时针旋转60°得到CD ，连接OD ， AO ， BO ， AD ．

(1)、求证： $△$ BCO≌ $△$ ACD ．

(2)、若OA＝10，OB＝8，OC＝6，求∠BOC的度数．

查看试题解析
20. 某中学计划购买 $A$ 型和 $B$ 型课桌凳共 $200$ 套，经招标，购买一套 $A$ 型课桌凳比购买一套 $B$ 型课桌凳少用 $40$ 元，且购买 $4$ 套 $A$ 型和 $5$ 套 $B$ 型课桌凳共需 $1820$ 元．

(1)、求购买一套 $A$ 型课桌凳和一套 $B$ 型课桌凳各需多少元？

(2)、学校根据实际情况，要求购买这两种课桌凳总费用不能超过 $40880$ 元，求该校本次至少购买 $A$ 型课桌凳多少套？

查看试题解析
21. 如图，在Rt△ACB中，∠ACB=90°，D为AB中点，点E在直线BC上(点E不与点B，C重合)，连接DE，过点D作DF⊥DE交直线AC于点F，连接EF．

(1)、如图(a)，当点F与点A重合时，请直接写出线段EF与BE的数量关系：

(2)、如图(b)，当点F不与点A重合时，证明：AF²+BE²=EF²；

(3)、若AC=5，BC=3，EC=1，请直接写出线段AF的长．

查看试题解析
22. 综合实践
在学习全等三角形的知识时，数学兴趣小组发现这样一个模型：它是由两个共顶点且顶角相等的等腰三角形构成的，在相对位置变化的同时，适中存在一对全等三角形，兴趣小组成员经过研讨给出定义：如果两个等腰三角形的顶角相等，且顶角的顶点互相重合，则称此图形为“手拉手全等模型”．因为顶点相连的四条边，可以形象地看作两双手，所以通常称为“手拉手模型”，如图1，△ABC与△ADE都是等腰三角形，其中∠BAC＝∠DAE，则△ABD≌△ACE（SAS）．

(1)、[初步把握]如图2，△ABC与△ADE都是等腰三角形，AB＝AC，且∠BAC＝∠DAE，则有 ≌ ．

(2)、[深入研究]如图3，已知△ABC，以AB、AC为边分别向外作等边△ABD和等边△ACE，并连接BE、CD，求证：BE＝CD．

(3)、[拓展延伸]如图4，在两个等腰直角三角形△ABC和△ADE中，AB＝AC，AE=AD，∠BAC＝∠DAE＝90°，连接BD，CE，交于点P，请判断BD和CE的关系，并说明理由.

查看试题解析