2024年浙教版数学八年级下学期阶段训练-特殊平行四边形
试卷更新日期:2024-04-13 类型:复习试卷
一、选择题(每题3分,共36分)
-
1. 如图,平行四边形ABCD中,EF过对角线的交点O,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )
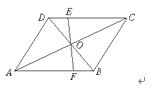 A、8.3 B、9.6 C、12.6 D、13.62. 如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC和∠BCD的角平分线分别交AD于点E和F,若BE=6,则CF=( )
A、8.3 B、9.6 C、12.6 D、13.62. 如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC和∠BCD的角平分线分别交AD于点E和F,若BE=6,则CF=( ) A、6 B、8 C、10 D、133. 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E,F,G,H分别是AB,AC,CD,BD的中点,则四边形EFGH的周长是( ).
A、6 B、8 C、10 D、133. 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E,F,G,H分别是AB,AC,CD,BD的中点,则四边形EFGH的周长是( ).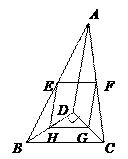 A、12 B、11 C、10 D、94. 如图,已知▱OABC的顶点A,C分别在直线 和 上,O是坐标原点,则对角线OB长的最小值为( )
A、12 B、11 C、10 D、94. 如图,已知▱OABC的顶点A,C分别在直线 和 上,O是坐标原点,则对角线OB长的最小值为( )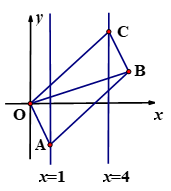 A、3 B、4 C、5 D、65. 已知点D与点 A(8,0),B(0,6),C(a,-a)是一平行四边形的四个顶点,则CD长的最小值为( )
A、3 B、4 C、5 D、65. 已知点D与点 A(8,0),B(0,6),C(a,-a)是一平行四边形的四个顶点,则CD长的最小值为( )
A、8 B、7 C、66. 如图,平行四边形ABCD中,对角线AC、BD相交于O,BD=2AD,E,F,G分别是OC,OD,AB的中点,下列结论:①四边形BEFG是平行四边形;②BE⊥AC;③EG=FG;④EA平分∠GEF。其中正确的是( ) A、①② B、①②③ C、①②④ D、①③④7. 如图,在中, , D、E分别为、的中点,平分 , 交于点F,若 , , 则的长为( )
A、①② B、①②③ C、①②④ D、①③④7. 如图,在中, , D、E分别为、的中点,平分 , 交于点F,若 , , 则的长为( ) A、2 B、1 C、4 D、8. 在矩形ABCD中,AB=1,AD= , AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
A、2 B、1 C、4 D、8. 在矩形ABCD中,AB=1,AD= , AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( ) A、1个 B、2个 C、3个 D、4个9. 如图,两个全等的矩形AEFG,矩形ABCD如图所示放置.CD所在直线与AE,GF分别交于点H,M.若AB=3,BC= ,CH=MH.则线段MH的长度是( )
A、1个 B、2个 C、3个 D、4个9. 如图,两个全等的矩形AEFG,矩形ABCD如图所示放置.CD所在直线与AE,GF分别交于点H,M.若AB=3,BC= ,CH=MH.则线段MH的长度是( ) A、 B、 C、 D、210. 如图,在矩形 中, , 的平分线交边 于点 , 于点 ,连接 并延长交边 于点 ,连接 交 于点 .给出下列命题:① ;② ;③ ;④ .其中正确命题为( )
A、 B、 C、 D、210. 如图,在矩形 中, , 的平分线交边 于点 , 于点 ,连接 并延长交边 于点 ,连接 交 于点 .给出下列命题:① ;② ;③ ;④ .其中正确命题为( ) A、①② B、①③ C、①③④ D、①②③④11. 如图,在矩形 中,点 在 边上, 于 ,若 , ,则线段 的长是( )
A、①② B、①③ C、①③④ D、①②③④11. 如图,在矩形 中,点 在 边上, 于 ,若 , ,则线段 的长是( ) A、5 B、4 C、 D、12. 如图,在 中, , , .分别以点B、D为圆心,大于 长为半径画弧,两弧相交于点M、N,直线MN分别与AD、BC相交于点E、F,则EF的长为( )
A、5 B、4 C、 D、12. 如图,在 中, , , .分别以点B、D为圆心,大于 长为半径画弧,两弧相交于点M、N,直线MN分别与AD、BC相交于点E、F,则EF的长为( ) A、 B、4 C、 D、
A、 B、4 C、 D、二、填空题(每题3分,共45分)
-
13.
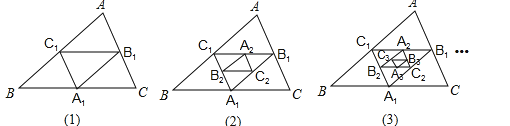
如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有个
 14. 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=3,则DF的长为 .
14. 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=3,则DF的长为 .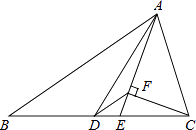 15. 如图,在△ABC中,AB=AC=6,中线CE=5.延长AB到点D,使BD=AB,则CD的长.
15. 如图,在△ABC中,AB=AC=6,中线CE=5.延长AB到点D,使BD=AB,则CD的长. 16. 如图四边形ABCD , AD∥BC , AB⊥BC , AD=1,AB=2,BC=3,P为AB边上的一动点,以PD , PC为边作平行四边形PCQD , 则对角线PQ的长的最小值是.
16. 如图四边形ABCD , AD∥BC , AB⊥BC , AD=1,AB=2,BC=3,P为AB边上的一动点,以PD , PC为边作平行四边形PCQD , 则对角线PQ的长的最小值是. 17. 如图, 中, ,以AB为边在三角形外的 的对角线交于点F,AE=2,AB=5,则CF的最大值是 .
17. 如图, 中, ,以AB为边在三角形外的 的对角线交于点F,AE=2,AB=5,则CF的最大值是 .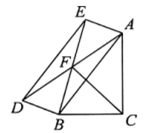 18. 如图,在▱ 中, 是对角线, ,点 是 的中点, 平分 , 于点 ,连接 已知 , ,则 的长为.
18. 如图,在▱ 中, 是对角线, ,点 是 的中点, 平分 , 于点 ,连接 已知 , ,则 的长为. 19. 如图在平行四边形ABCD中,∠ABC=60°,AB=4,四条内角平分线围成四边形EFGH面积为 , 则平行四边形ABCD面积为
19. 如图在平行四边形ABCD中,∠ABC=60°,AB=4,四条内角平分线围成四边形EFGH面积为 , 则平行四边形ABCD面积为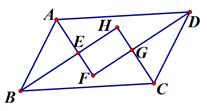 20. 如图,在中,点 , 分别为 , 的中点,平分 , 交于点 , 连接并延长交于 , 已知 , , , 则 .
20. 如图,在中,点 , 分别为 , 的中点,平分 , 交于点 , 连接并延长交于 , 已知 , , , 则 . 21. 如图,在平行四边形ABCD中, , 对角线AC、BD交于点 , 经过点的直线交AD于点 , 且平分的周长,则.
21. 如图,在平行四边形ABCD中, , 对角线AC、BD交于点 , 经过点的直线交AD于点 , 且平分的周长,则. 22. 如图,矩形ABCD中,AC、BD交于点O,∠AOB=60°,DE平分∠ADC交BC于点E,连接OE,则∠COE= .
22. 如图,矩形ABCD中,AC、BD交于点O,∠AOB=60°,DE平分∠ADC交BC于点E,连接OE,则∠COE= . 23. 如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为 .
23. 如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为 . 24. 如图,在矩形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME=15°,则∠ABE=
24. 如图,在矩形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME=15°,则∠ABE= 25. 如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交BC、AD于点E、F,若BE=3,AF=5,则AC的长为.
25. 如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交BC、AD于点E、F,若BE=3,AF=5,则AC的长为. 26. 如图①是一张等腰直角三角形纸片, , 现要求按照图②的方法裁剪几条宽度都为的长方形纸条,用这些纸条为一幅正方形美术作品EFGH镶边(纸条不重叠)如图③,正方形美术作品的面积为.
26. 如图①是一张等腰直角三角形纸片, , 现要求按照图②的方法裁剪几条宽度都为的长方形纸条,用这些纸条为一幅正方形美术作品EFGH镶边(纸条不重叠)如图③,正方形美术作品的面积为. 27. 新定义:关于的一元二次方程与称为“同族二次方程”.例如:与是“同族二次方程”.现有关于的一元二次方程与是“同族二次方程”,则代数式的最小值是.
27. 新定义:关于的一元二次方程与称为“同族二次方程”.例如:与是“同族二次方程”.现有关于的一元二次方程与是“同族二次方程”,则代数式的最小值是.三、解答题(共2题,共10分)
-
28. 如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
 29. 如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
29. 如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?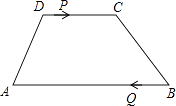
四、综合题(共3题,共29分)
-
30. 如图

 (1)、如图1,在▱ABCD中,AE平分∠BAD交CD边于点E,已知AB=5cm,AD=3cm,则EC等于cm。(2)、如图2,在▱ABCD中,若AE,BE分别是∠DAB,∠CBA的平分线,点E在DC边上,且AB=4,则ABCD的周长为。(3)、如图3,已知四边形ABCD是平行四边形,AD=BC,若AF,BE分别是∠DAB,∠CBA的平分线。求证:DF=EC(4)、在(3)的条件下,如果AD=3,AB=5,则EF的长为。31. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)、如图1,在▱ABCD中,AE平分∠BAD交CD边于点E,已知AB=5cm,AD=3cm,则EC等于cm。(2)、如图2,在▱ABCD中,若AE,BE分别是∠DAB,∠CBA的平分线,点E在DC边上,且AB=4,则ABCD的周长为。(3)、如图3,已知四边形ABCD是平行四边形,AD=BC,若AF,BE分别是∠DAB,∠CBA的平分线。求证:DF=EC(4)、在(3)的条件下,如果AD=3,AB=5,则EF的长为。31. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF. (1)、求证:四边形ADFE是矩形;(2)、连接OF,若AD=6,EC=4,∠ABF=60°,求OF的长度.32. 阅读材料:
(1)、求证:四边形ADFE是矩形;(2)、连接OF,若AD=6,EC=4,∠ABF=60°,求OF的长度.32. 阅读材料:已知a,b为非负实数,
, 当且仅当“”时,等号成立.
这个结论就是著名的“均值不等式”,“均值不等式”在一类最值问题中有着广泛的应用.
例:已知 , 求代数式最小值.
解:令 , 则由 , 得.
当且仅当 , 即时,代数式取到最小值,最小值为6.
根据以上材料解答下列问题:
(1)、【灵活运用】已知 , 则当时,代数式取到最小值,最小值为.
(2)、已知 , 求代数式的最小值.(3)、【拓展运用】某校要对操场的一个区域进行改造,利用一面足够长的墙体将该区域用围栏围成中间隔有两道围栏的矩形花圃,如图1所示,为了围成面积为的花圃,所用的围栏至少为多少米?
 (4)、如图2,四边形ABCD的对角线AC,BD相交于点和的面积分别是4和12,求四边形ABCD面积的最小值.
(4)、如图2,四边形ABCD的对角线AC,BD相交于点和的面积分别是4和12,求四边形ABCD面积的最小值.