2024年浙教版数学初中学业水平考试模拟试题
试卷更新日期:2024-04-13 类型:中考模拟
一、选择题(每题3分,共30分)
-
1. 用 , , , 这四个数进行如下运算,计算结果最小的式子是( )A、 B、 C、 D、2. 某物体如图所示,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 某校计划组织研学活动,现有四个地点可供选择:南麂岛、百丈漈、楠溪江、雁荡山.为了解学生想法,校方进行问卷调查(每人选一个地点),并绘制成如图所示的统计图,已知选择雁荡山的有270人,则选择楠溪江的有( )
3. 某校计划组织研学活动,现有四个地点可供选择:南麂岛、百丈漈、楠溪江、雁荡山.为了解学生想法,校方进行问卷调查(每人选一个地点),并绘制成如图所示的统计图,已知选择雁荡山的有270人,则选择楠溪江的有( )某校学生最想去的研学地点统计图
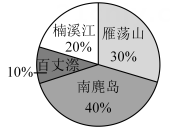 A、90人 B、180人 C、270人 D、360人4. 下列计算正确的是( )A、 B、 C、 D、5. 下列说法中,正确的是( )A、“任意画一个三角形,其内角和为180°”是必然事件 B、调查全国中学生的视力情况,适合采用普查的方式 C、抽样调查的样本容量越小,对总体的估计就越准确 D、十字路口的交通信号灯有红、黄、绿三种颜色,所以开车经过十字路口时,恰好遇到黄灯的概率为6. 关于x的一元二次方程有两个不相等的实数根,则m的取值范围是( )A、 B、m>3 C、m≤3 D、m<37. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返的速度大小不变,两车离甲地的距离y(km)与慢车行驶时间t(h)的函数关系如图所示,则两车先后两次相遇的间隔时间是( )
A、90人 B、180人 C、270人 D、360人4. 下列计算正确的是( )A、 B、 C、 D、5. 下列说法中,正确的是( )A、“任意画一个三角形,其内角和为180°”是必然事件 B、调查全国中学生的视力情况,适合采用普查的方式 C、抽样调查的样本容量越小,对总体的估计就越准确 D、十字路口的交通信号灯有红、黄、绿三种颜色,所以开车经过十字路口时,恰好遇到黄灯的概率为6. 关于x的一元二次方程有两个不相等的实数根,则m的取值范围是( )A、 B、m>3 C、m≤3 D、m<37. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返的速度大小不变,两车离甲地的距离y(km)与慢车行驶时间t(h)的函数关系如图所示,则两车先后两次相遇的间隔时间是( )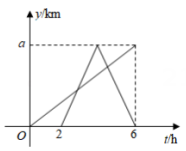 A、h B、h C、h D、h8. 如图,是一张周长为的三角形纸片,是它的内切圆,小明准备用剪刀在的右侧沿着与相切的任意一条直线MN剪下 , 则剪下的三角形的周长为( )
A、h B、h C、h D、h8. 如图,是一张周长为的三角形纸片,是它的内切圆,小明准备用剪刀在的右侧沿着与相切的任意一条直线MN剪下 , 则剪下的三角形的周长为( ) A、13cm B、8cm C、6.5cm D、随直线MN的变化而变化9. 二次函数y=ax2-2x+1和一次函数y=ax-a(a是常数,且a≠0)在同一平面直角坐标系的图象可能是( )A、
A、13cm B、8cm C、6.5cm D、随直线MN的变化而变化9. 二次函数y=ax2-2x+1和一次函数y=ax-a(a是常数,且a≠0)在同一平面直角坐标系的图象可能是( )A、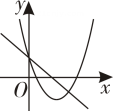 B、
B、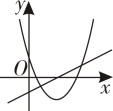 C、
C、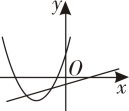 D、
D、 10. 如图,在中,是边上的点(不与点重合).过点作交于点;过点作交于点.是线段上的点,;是线段上的点,.若已知的面积,则一定能求出( )
10. 如图,在中,是边上的点(不与点重合).过点作交于点;过点作交于点.是线段上的点,;是线段上的点,.若已知的面积,则一定能求出( ) A、的面积 B、的面积 C、的面积 D、的面积
A、的面积 B、的面积 C、的面积 D、的面积二、填空题(每题4分,共24分)
-
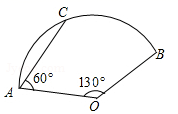
11. 分解因式: =.12. 不等式组的解是。13. 定义一种新运算:对于任意的非零实数a,b,a b= .若(x+1) x= ,则x的值为14. 如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则 的长为 .
 15. 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y= (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
15. 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y= (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .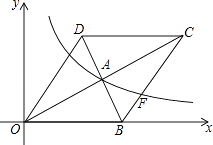 16. 图1是一折叠桌,桌板DEIJ固定在墙上,支架AD,HE绕点D,E旋转时,AD∥HE,桌板边缘AH∥BG∥CF∥DE,桌脚AN.⊥AH,桌子放平得图2.图3是打开过程中侧面视图,当点N在直线CF上时,点N到墙OE的距离为cm.视图中以C,K为顶点的长方形表示一圆柱体花瓶,桌子打开至点M,C,F在同一直线时,桌板边缘GL恰好卡在点K,为不影响桌板BG收放,则至少将花瓶沿CF方向平移cm.
16. 图1是一折叠桌,桌板DEIJ固定在墙上,支架AD,HE绕点D,E旋转时,AD∥HE,桌板边缘AH∥BG∥CF∥DE,桌脚AN.⊥AH,桌子放平得图2.图3是打开过程中侧面视图,当点N在直线CF上时,点N到墙OE的距离为cm.视图中以C,K为顶点的长方形表示一圆柱体花瓶,桌子打开至点M,C,F在同一直线时,桌板边缘GL恰好卡在点K,为不影响桌板BG收放,则至少将花瓶沿CF方向平移cm.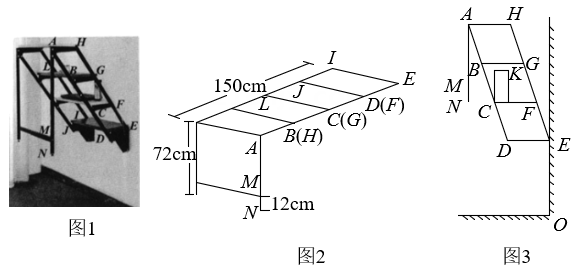
三、解答题(共8题,共66分)
-
17. 计算:.18. 图①、图②均是的正方形网格,每个小正方形的顶点称为格点,线段的端点均在格点上.只用无刻度的直尺按下列要求在给定的网格中画图.(不要求写画法,但需保留作图痕迹.)
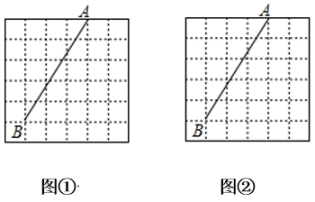 (1)、在图中画出线段的中点;(2)、在图中画出线段上的一点 , 使:: .19. 在一个不透明的口袋中装有4张相同的纸牌,它们分别标有数字1,2,3,4,随机地摸取两张纸牌,请用列表或画树状图的方法解决下列问题.(1)、计算摸取的两张纸牌上数字之和为5的概率;(2)、甲、乙两人进行游戏,如果摸取的两张纸牌上数字之和为奇数,则甲胜;如果摸取的两张纸牌上数字之和为偶数,则乙胜.这个游戏公平吗?请说明理由.20. 如图,四边形是平行四边形, , 且分别交对角线于点M , N , 连接 .
(1)、在图中画出线段的中点;(2)、在图中画出线段上的一点 , 使:: .19. 在一个不透明的口袋中装有4张相同的纸牌,它们分别标有数字1,2,3,4,随机地摸取两张纸牌,请用列表或画树状图的方法解决下列问题.(1)、计算摸取的两张纸牌上数字之和为5的概率;(2)、甲、乙两人进行游戏,如果摸取的两张纸牌上数字之和为奇数,则甲胜;如果摸取的两张纸牌上数字之和为偶数,则乙胜.这个游戏公平吗?请说明理由.20. 如图,四边形是平行四边形, , 且分别交对角线于点M , N , 连接 .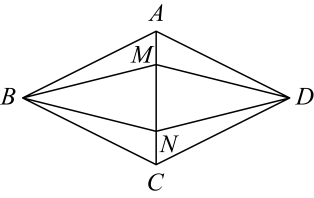 (1)、求证:;(2)、若 . 求证:四边形是菱形.21. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 抛物线经过 , 两点,与轴的另一个交点为点 .
(1)、求证:;(2)、若 . 求证:四边形是菱形.21. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 抛物线经过 , 两点,与轴的另一个交点为点 .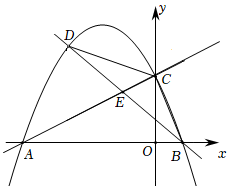 (1)、求抛物线的函数表达式.(2)、点为直线上方抛物线上一动点,连接 , , 设直线交线段于点 , 的面积为 , 的面积为 , 求的最大值.22. 如图1,某款线上教学设备由底座,支撑臂 , 连杆 , 悬臂和安装在处的摄像头组成.如图2是该款设备放置在水平桌面上的示意图,已知支撑臂 , , 固定 , 可通过调试悬臂与连杆的夹角提高拍摄效果.
(1)、求抛物线的函数表达式.(2)、点为直线上方抛物线上一动点,连接 , , 设直线交线段于点 , 的面积为 , 的面积为 , 求的最大值.22. 如图1,某款线上教学设备由底座,支撑臂 , 连杆 , 悬臂和安装在处的摄像头组成.如图2是该款设备放置在水平桌面上的示意图,已知支撑臂 , , 固定 , 可通过调试悬臂与连杆的夹角提高拍摄效果.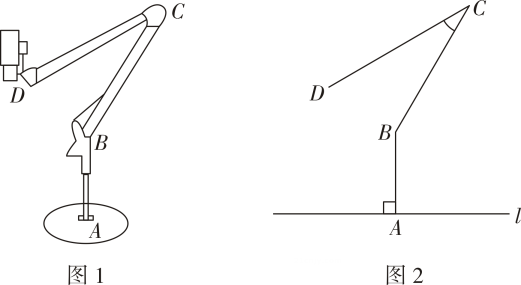 (1)、当悬臂与桌面平行时,=°(2)、问悬臂端点到桌面的距离约为多少?(3)、已知摄像头点到桌面的距离为30cm时拍摄效果较好,那么此时悬臂与连杆的夹角的度数约为多少?(参考数据:)23. 根据以下素材,探究完成任务
(1)、当悬臂与桌面平行时,=°(2)、问悬臂端点到桌面的距离约为多少?(3)、已知摄像头点到桌面的距离为30cm时拍摄效果较好,那么此时悬臂与连杆的夹角的度数约为多少?(参考数据:)23. 根据以下素材,探究完成任务素材1 图1是一个瓷碗,图2是其截面图,碗体DEC呈抛物线状(碗体厚度不计),碗高GF=7cm,碗底宽AB=3cm,当瓷碗中装满面汤时,液面宽CD= 12cm,
此时面汤最大深度EG= 6cm,
素材2 如图3,把瓷碗绕点B缓缓倾斜倒出部分面汤,当点A离MN距离为1.8cm时停止.

问题解决 任务1 确定碗体形状 在图2中建立合适的直角坐标系,求抛物线的函数表达式。
任务2 拟定设计方案1 根据图2位置,把碗中面汤喝掉一部分,当碗中液面高度(离桌面MN距离)为5cm时,求此时碗中液面宽度。
任务3 拟定设计方案2 如图3,当碗停止倾斜时,求此时碗中液面宽度CH。
24. 小贺在复习浙教版教材九上第81页第5题后,进行变式、探究与思考:如图1,的直径垂直弦AB于点E , 且 , .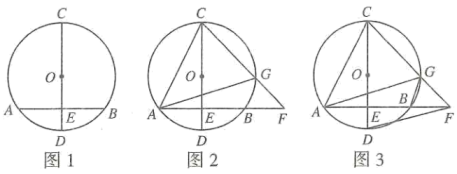 (1)、复习回顾:求的长.(2)、探究拓展:如图2,连接 , 点G是上一动点,连接 , 延长交的延长线于点F .
(1)、复习回顾:求的长.(2)、探究拓展:如图2,连接 , 点G是上一动点,连接 , 延长交的延长线于点F .①当点G是的中点时,求证:;
②设 , , 请写出y关于x的函数关系式,并说明理由;
③如图3,连接 , 当为等腰三角形时,请计算的长.