2024年初中数学人教版八年级下学期期中模拟考试卷 02
试卷更新日期:2024-04-13 类型:期中考试
一、单选题
-
1. 下列二次根式中,不能与合并的是( )A、 B、 C、 D、2. 已知,中的对边分别是a、b、c,下列条件不能判断是直角三角形的是( )A、 B、 , , C、 D、3. 已知实数a在数轴上的位置如图所示,则化简:的结果为( )
 A、2 B、 C、 D、4. 下列命题中正确的是( )A、平行四边形的对角线互相垂直 B、矩形的对角线相等 C、对角线相等的平行四边形是菱形 D、对角线互相垂直的平行四边形是正方形5. 如图,在中, , , , 是斜边的高,则的长为( )
A、2 B、 C、 D、4. 下列命题中正确的是( )A、平行四边形的对角线互相垂直 B、矩形的对角线相等 C、对角线相等的平行四边形是菱形 D、对角线互相垂直的平行四边形是正方形5. 如图,在中, , , , 是斜边的高,则的长为( ) A、 B、 C、5 D、106. 如图,Rt△ABC中, ∠ACB=90°,∠A=30°,CD⊥AB于D,CE是△ABC的中线,要说明“三个角分别对应相等的两个三角形全等”是假命题,可以作为反例的两个三角形是( )
A、 B、 C、5 D、106. 如图,Rt△ABC中, ∠ACB=90°,∠A=30°,CD⊥AB于D,CE是△ABC的中线,要说明“三个角分别对应相等的两个三角形全等”是假命题,可以作为反例的两个三角形是( ) A、△ACE和△BCE B、△BCE和△ABC C、△CDE 和△BCD D、△ACD和△BCD7. 如图,在中,连接 , , , 则的度数是( )
A、△ACE和△BCE B、△BCE和△ABC C、△CDE 和△BCD D、△ACD和△BCD7. 如图,在中,连接 , , , 则的度数是( ) A、 B、 C、 D、8. 如图,“赵爽弦图”是一个由四个全等的直角三角形和一个小正方形拼接成的大正方形,若E是AF的中点, , 连接BF并延长交CD于点M , 则DM的长为( )
A、 B、 C、 D、8. 如图,“赵爽弦图”是一个由四个全等的直角三角形和一个小正方形拼接成的大正方形,若E是AF的中点, , 连接BF并延长交CD于点M , 则DM的长为( ) A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
9. 一个长方形的面积为 , 已知这个长方形的长为 , 则宽为 .10. 若在实数范围内有意义,则的取值范围为.11. 小明设计了测量池塘两端AB距离的方案,如图,先取一点C,连结AC,BC,再取它们的中点D,E,测得DE=15米,则AB=米.
 12. 如图所示,四边形ABCD是边长为2的菱形, , 则四边形ABCD的面积为 .
12. 如图所示,四边形ABCD是边长为2的菱形, , 则四边形ABCD的面积为 . 13. 已知菱形的两条对角线长分别为6和8,则它的面积为 .14. 如图,在和中, , 点在边的中点上,若 , , 连结 , 则的长为 .
13. 已知菱形的两条对角线长分别为6和8,则它的面积为 .14. 如图,在和中, , 点在边的中点上,若 , , 连结 , 则的长为 .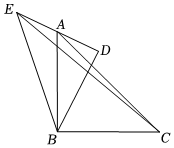 15. 如图,在矩形中, , , 为边的中点,点在线段上运动,是的中点,则的周长的最小值是.
15. 如图,在矩形中, , , 为边的中点,点在线段上运动,是的中点,则的周长的最小值是. 16. 如图,已知四边形ABCD为正方形, , E为对角线AC上一点,连接DE , 过点E作EF⊥DE , 交BC的延长线于点F , 以DE , EF为邻边作矩形DEFG , 连接CG . 下列结论:①矩形DEFG是正方形;②;③CG平分∠DCF;④CE=CF . 其中正确的是 (填序号).
16. 如图,已知四边形ABCD为正方形, , E为对角线AC上一点,连接DE , 过点E作EF⊥DE , 交BC的延长线于点F , 以DE , EF为邻边作矩形DEFG , 连接CG . 下列结论:①矩形DEFG是正方形;②;③CG平分∠DCF;④CE=CF . 其中正确的是 (填序号).
三、解答题
-
17. 一艘轮船从港向南偏西方向航行到达岛,再从岛沿方向航行到达岛,港到航线的最短距离是 .
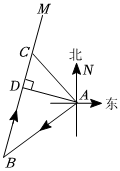 (1)、若轮船速度为小时,求轮船从岛沿返回港所需的时间.(2)、求岛在港的什么方向?18. 如图,点 E,F 分别在▱ABCD 的边 BC,AD 连结 BF,DE.求证:四边形 BEDF 是平行四边形.
(1)、若轮船速度为小时,求轮船从岛沿返回港所需的时间.(2)、求岛在港的什么方向?18. 如图,点 E,F 分别在▱ABCD 的边 BC,AD 连结 BF,DE.求证:四边形 BEDF 是平行四边形. 19. 如图,在四边形中,对角线 , 交于点 , , .
19. 如图,在四边形中,对角线 , 交于点 , , .
 (1)、求证:;(2)、过点作 , 垂足为点 , 求证:;(3)、点为上一点,连接 , , , , 若 , , 求线段的长.
(1)、求证:;(2)、过点作 , 垂足为点 , 求证:;(3)、点为上一点,连接 , , , , 若 , , 求线段的长.四、实践探究题
-
20. 【阅读材料】小明在学习二次根式时,发现一些含根号的式子可以化成另一个式子的平方,如:
;
.
【类比归纳】
(1)、小华仿照小明的方法将化成了 , 则 , .(2)、请运用小明的方法化简 .(3)、【拓展提升】计算 .
21. 如图,在中, , , 点以每秒的速度由点向点运动不与点重合 , 过点作直线 , 的外角平分线于点 , 的平分线于点设运动时间为秒. (1)、发现:
(1)、发现:①在点的运动过程中,与的关系是 ▲ , 请写出理由.
②当时, ▲ .
(2)、探究:当 ▲ 时,四边形是矩形,并证明你的结论.(3)、拓展:若点在运动过程中,能使四边形是正方形,试写出线段的长度.直接写出结论即可五、综合题


