2024年初中数学人教版八年级下学期期中模拟考试卷 01
试卷更新日期:2024-04-13 类型:期中考试
一、单选题
-
1. 下列各式中,属于最简二次根式的是( )A、 B、 C、 D、2. 在下列四组数中,属于勾股数的是( )A、0.3,0.4,0.5 B、9,40,41 C、6,7,8 D、1, ,3. 已知 , 那么的取值范围是( )A、 B、 C、 D、4. 如图,四边形是菱形,过点的直线分别交 , 的延长线于点 , , 若 , , 则等于( )
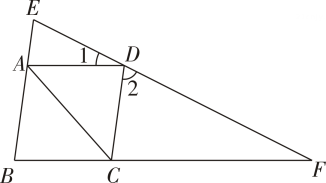 A、 B、 C、 D、5. 二次根式 中,字母a的取值范围是( )A、 B、 C、 D、6. 如图,在中, , 是边上的高,若 , 则( )
A、 B、 C、 D、5. 二次根式 中,字母a的取值范围是( )A、 B、 C、 D、6. 如图,在中, , 是边上的高,若 , 则( ) A、2 B、2.4 C、3 D、7. 如图所示,点是矩形对角线的中点,交于点若 , , 则的长为( )
A、2 B、2.4 C、3 D、7. 如图所示,点是矩形对角线的中点,交于点若 , , 则的长为( )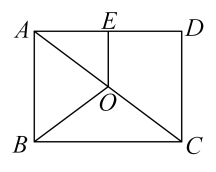 A、 B、 C、 D、8. 在△ABC中a , b , c分别是∠A、∠B , ∠C的对边,下列条件中,不能判断△ABC是直角三角形的是( )A、a:b:c=5:12:13 B、 C、∠A:∠B:∠C=3:4:5 D、∠A+∠B=∠C9. 在平行四边形中,对角线 , 相交于点O, , , 则边的长度x的取值范围是( )A、 B、 C、 D、10. 如图,在矩形ABCD中,O为对角线BD的中点,∠ABD=60°,动点E在线段OB上,动点F在线段OD上,点E,F同时从点O出发,分别向终点B,D运动,且始终保持OE=OF.点E关于AD ,AB的对称点为E1 , E2;点F关于BC,CD的对称点为F1 , F2 , 在整个过程中,四边形E1E2F1F2形状的变化依次是( )
A、 B、 C、 D、8. 在△ABC中a , b , c分别是∠A、∠B , ∠C的对边,下列条件中,不能判断△ABC是直角三角形的是( )A、a:b:c=5:12:13 B、 C、∠A:∠B:∠C=3:4:5 D、∠A+∠B=∠C9. 在平行四边形中,对角线 , 相交于点O, , , 则边的长度x的取值范围是( )A、 B、 C、 D、10. 如图,在矩形ABCD中,O为对角线BD的中点,∠ABD=60°,动点E在线段OB上,动点F在线段OD上,点E,F同时从点O出发,分别向终点B,D运动,且始终保持OE=OF.点E关于AD ,AB的对称点为E1 , E2;点F关于BC,CD的对称点为F1 , F2 , 在整个过程中,四边形E1E2F1F2形状的变化依次是( ) A、菱形→平行四边形→矩形→平行四边形→菱形 B、菱形→正方形→平行四边形→菱形→平行四边形 C、平行四边形→矩形→平行四边形→菱形→平行四边形 D、平行四边形→菱形→正方形→平行四边形→菱形
A、菱形→平行四边形→矩形→平行四边形→菱形 B、菱形→正方形→平行四边形→菱形→平行四边形 C、平行四边形→矩形→平行四边形→菱形→平行四边形 D、平行四边形→菱形→正方形→平行四边形→菱形二、填空题
-
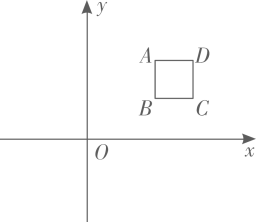
11. 若代数式有意义,则x的取值范围式.12. 如图,平面直角坐标系中,正方形边长为1个单位长度,若轴,且点的坐标是 , 则点的坐标为 .
 13. 已知一个直角三角形的两条直角边分别为6,8,那么这个直角三角形斜边上的高为 .14. 如图,中, , 于点 , 平分 , 交与点 , 于点 , 且交于点 , 若 , , 则 .
13. 已知一个直角三角形的两条直角边分别为6,8,那么这个直角三角形斜边上的高为 .14. 如图,中, , 于点 , 平分 , 交与点 , 于点 , 且交于点 , 若 , , 则 . 15. 如图,四边形中, , , , , 其中 , 则四边形的面积是 .
15. 如图,四边形中, , , , , 其中 , 则四边形的面积是 .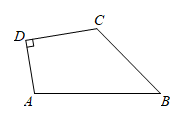 16. 如图,在边长为的正方形中,点在边上,且点是边上的动点,连接 , 将线段绕点顺时针旋转得到线段若在正方形内还存在一点 , 则点到点、点、点的距离之和的最小值为 .
16. 如图,在边长为的正方形中,点在边上,且点是边上的动点,连接 , 将线段绕点顺时针旋转得到线段若在正方形内还存在一点 , 则点到点、点、点的距离之和的最小值为 .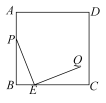
三、解答题
-
17. 已知四边形是平行四边形,点在对角线上,点在边上,连接 , , .
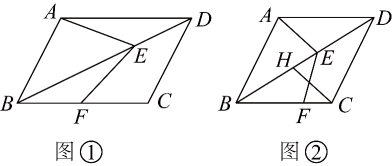 (1)、如图①,求证;(2)、如图②,若 , 过点作交于点 , 在不添加任何辅助线的情况下,请直接写出图②中四个角(除外),使写出的每个角都与相等.18. 如图,四边形中, , , , 垂足分别为 , .
(1)、如图①,求证;(2)、如图②,若 , 过点作交于点 , 在不添加任何辅助线的情况下,请直接写出图②中四个角(除外),使写出的每个角都与相等.18. 如图,四边形中, , , , 垂足分别为 , . (1)、求证:四边形是矩形;(2)、若 , , , 点是的中点,请直接写出的长19. 如图,正方形 ABCD 的边长为4,E 为BC 边上的一点,BE=1,F为AB 的中点.若 P 为对角线AC 上的一个动点,求 PF+PE的最小值.
(1)、求证:四边形是矩形;(2)、若 , , , 点是的中点,请直接写出的长19. 如图,正方形 ABCD 的边长为4,E 为BC 边上的一点,BE=1,F为AB 的中点.若 P 为对角线AC 上的一个动点,求 PF+PE的最小值.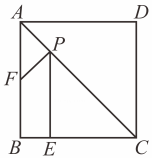
四、实践探究题
-
20. 【阅读材料】小明在学习二次根式时,发现一些含根号的式子可以化成另一个式子的平方,
如:
(1)、【类比归纳】
请你仿照小明的方法将化成另一个式子的平方.(2)、【变式探究】
若且a,m,n均为正整数,求a值.21. 如图①,把两个边长为的小正方形沿对角线剪开,所得的个直角三角形拼成一个面积为的大正方形.由此得到了一种能在数轴上画出无理数对应点的方法.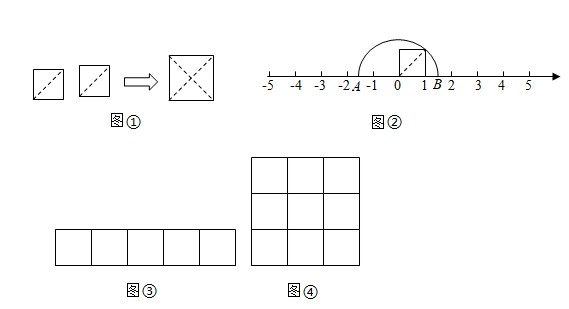 (1)、图②中、两点表示的数分别为 , ;(2)、请你参照上面的方法:
(1)、图②中、两点表示的数分别为 , ;(2)、请你参照上面的方法:把图③中的长方形进行剪裁,并拼成一个大正方形.在图③中画出裁剪线,并在图④的正方形网格中画出拼成的大正方形,该正方形的边长 ▲ . (注:小正方形边长都为 , 拼接不重叠也无空隙)
五、综合题
-
22. 某校的九(1)班教室A位于工地B处的正东方向,且米,一辆大型货车卸货后从B处出发,沿北偏东方向的公路上行驶,试问:
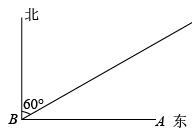 (1)、若大型货车的噪声污染半径为150米,教室A是否在大型货车的噪声污染范围内?试说明理由;(2)、若大型货车的噪声污染半径为200米,为了不干扰九年级同学的学习,计划在货车行驶的公路一侧安装隔音板,则至少需隔音板多少米?23. 如图,在中, , 延长至D,使得 , 过点A,D分别作 , , 与相交于点E.下面是两位同学的对话:
(1)、若大型货车的噪声污染半径为150米,教室A是否在大型货车的噪声污染范围内?试说明理由;(2)、若大型货车的噪声污染半径为200米,为了不干扰九年级同学的学习,计划在货车行驶的公路一侧安装隔音板,则至少需隔音板多少米?23. 如图,在中, , 延长至D,使得 , 过点A,D分别作 , , 与相交于点E.下面是两位同学的对话: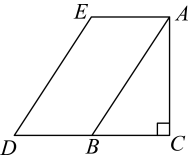

小星:由题目的已知条件,若连接 , 则可
证明 .
小红:由题目的已知条件,若连接 , 则可证明 .
 (1)、请你选择一位同学的说法,并进行证明;(2)、连接 , 若 , 求的长.
(1)、请你选择一位同学的说法,并进行证明;(2)、连接 , 若 , 求的长.