2024年初中数学人教版七年级下学期期中模拟测试卷 03
试卷更新日期:2024-04-13 类型:期中考试
一、单选题
-
1. 在实数: , , , , , 0.1010010001…(每2个1之间依次多一个0)中,无理数的个数是( )A、1个 B、2个 C、3个 D、4个2. 已知点 , , 将线段平移至 , 点的对应点在y轴上,点的对应点在x轴上,点的纵坐标为a,点的横坐标为b,则的值为( )A、 B、 C、 D、3. 下列各图中,∠1与∠2是对顶角的是( )A、
 B、
B、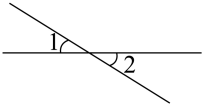 C、
C、 D、
D、 4. 如图所示,∠AOB的两边OA,OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,则∠ODE的度数是( )
4. 如图所示,∠AOB的两边OA,OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,则∠ODE的度数是( ) A、 B、 C、 D、5. 一把含45°角的三角尺和一把直尺按如图所示的方式摆放,若∠1=20°,则∠2的度数为( )
A、 B、 C、 D、5. 一把含45°角的三角尺和一把直尺按如图所示的方式摆放,若∠1=20°,则∠2的度数为( )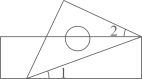 A、15° B、20° C、25° D、40°6. 数a,b在数轴上的对应点的位置如图所示.下列结论:①;②;③;④ . 其中,正确的有( )
A、15° B、20° C、25° D、40°6. 数a,b在数轴上的对应点的位置如图所示.下列结论:①;②;③;④ . 其中,正确的有( ) A、1个 B、2个 C、3个 D、4个7. 如图,直线// , 直角三角板ABC的直角顶点C在直线b上,若 , 则度数为( )
A、1个 B、2个 C、3个 D、4个7. 如图,直线// , 直角三角板ABC的直角顶点C在直线b上,若 , 则度数为( )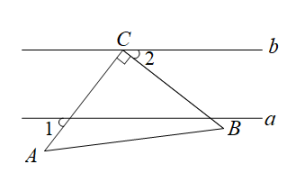 A、25° B、35° C、45° D、55°8. 如图,一只蚂蚁在平面直角坐标系中按箭头所示方向作折线运动,即第一次从原点运动到H(2,2),第二次从H(2,2)运动到I(4,6),第三次从I(4,6)运动到J(6,0),第四次从J(6,0)运动到K(8,2),第五次从K(8,2)运动到L(10,6)……,按这样的运动规律,经过2022次运动后,蚂蚁所处的坐标是( )
A、25° B、35° C、45° D、55°8. 如图,一只蚂蚁在平面直角坐标系中按箭头所示方向作折线运动,即第一次从原点运动到H(2,2),第二次从H(2,2)运动到I(4,6),第三次从I(4,6)运动到J(6,0),第四次从J(6,0)运动到K(8,2),第五次从K(8,2)运动到L(10,6)……,按这样的运动规律,经过2022次运动后,蚂蚁所处的坐标是( ) A、(4044,6) B、(2022,2) C、(4044,0) D、(2022,0)
A、(4044,6) B、(2022,2) C、(4044,0) D、(2022,0)二、填空题
-
9. 点A在第二象限,且它到x轴的距离是3个单位长度,到y轴的距离是4个单位长度,则点A的坐标为 .10. 如图, , , 平分 , 则的度数是.
 11. 已知点在轴上,则点的坐标是 .12. 如图 , , 为直线 , 上的两点,且 , , 则与的度数之和为 .
11. 已知点在轴上,则点的坐标是 .12. 如图 , , 为直线 , 上的两点,且 , , 则与的度数之和为 . 13. 如图,点C在直线上AB,CD平分∠ACE,若∠1=63°,则∠BCE的度数为度.
13. 如图,点C在直线上AB,CD平分∠ACE,若∠1=63°,则∠BCE的度数为度. 14. 图1是一盏可折叠台灯.图2,图3是其平面示意图,支架AB , BC为固定支撑杆,支架OC可绕点C旋转调节.已知灯体顶角∠DOE=48°,顶角平分线OP始终与OC垂直.当支架OC旋转至水平位置时(如图2),OD恰好与BC平行,则支架BC与水平方向的夹角∠θ=°;若将图2中的OC继续向上旋转10°(如图3),则此时OD与水平方向的夹角∠DQM=°.
14. 图1是一盏可折叠台灯.图2,图3是其平面示意图,支架AB , BC为固定支撑杆,支架OC可绕点C旋转调节.已知灯体顶角∠DOE=48°,顶角平分线OP始终与OC垂直.当支架OC旋转至水平位置时(如图2),OD恰好与BC平行,则支架BC与水平方向的夹角∠θ=°;若将图2中的OC继续向上旋转10°(如图3),则此时OD与水平方向的夹角∠DQM=°. 15. 如图,已知AB∥CD,E、F、H分别为AB、CD、AC上一点(∠DFK<∠BEK),KG平分∠EKF,∠AEK+∠HKE=180°.则下列结论:①CD∥KH;②∠BEK+∠DFK=2∠EKG;③∠BEK-∠DFK=∠GKH;④∠BAC+∠AGK-∠GKF+∠DFK=180°.其中正确的是 . (填序号)
15. 如图,已知AB∥CD,E、F、H分别为AB、CD、AC上一点(∠DFK<∠BEK),KG平分∠EKF,∠AEK+∠HKE=180°.则下列结论:①CD∥KH;②∠BEK+∠DFK=2∠EKG;③∠BEK-∠DFK=∠GKH;④∠BAC+∠AGK-∠GKF+∠DFK=180°.其中正确的是 . (填序号)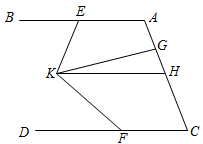
三、解答题
-
16. 如图,直线ABCD,直线EF分别交AB、CD于点M、N,∠CNF=40°,MG平分∠BMF,MG交CD于G,求∠EMB和∠MGN的度数.
 17. 阅读理解,补全证明过程及推理依据.
17. 阅读理解,补全证明过程及推理依据.已知:如图,点在直线上,点在直线上, , . 求证: .

证明:∵(已知)
( )
∴(等量代换)
∴( )
∴ ▲ (两直线平行,同旁内角互补)
又∵(已知)
∴ ▲ (等量代换)
∴ ▲ ▲ ( )
∴( )
18. 已知:如图,中, , 点、分别是 , 的中点,四边形是平行四边形吗?说说你的理由.
四、实践探究题
-
19. 阅读资料:在学习平行线知识的时候,小敏同学发现有的图形(如图1),不属于两条平行线被第三条直线所截的图形,不能直接应用平行线的性质解决问题.经过思考,小敏想到,若过点C作CF∥AB(如图2),这样就多了一个已知条件,问题就可以解决了.

请你参考小敏同学的方法,解决下面问题:
(1)、如图2,已知AB∥DE,用等式表示∠B,∠E,∠BCE之间的数量关系,并说明理由.(2)、如图3,已知AB∥DE,直接用等式表示出∠B,∠E,∠BCE之间的数量关系.五、综合题
-
20. 已知,直线 , 直线和 , 分别交于C,D点,点A,B分别在直线 , 上,且位于直线的左侧,动点P在直线上,且不和点C,D重合.
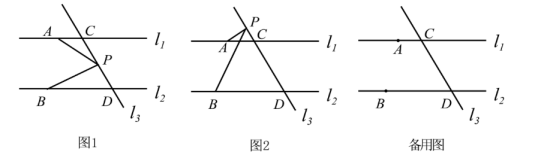 (1)、如图1,当动点P在线段CD上运动时,求证:∠APB=∠CAP+∠DBP;(2)、如图2,当动点P在点C上方运动时(P,A,B不在同一直线上),请写出∠APB,∠CAP,∠DBP之间的数量关系,并选择其中一种的数量关系说明理由.21.(1)、计算:;(2)、下面是小明同学解方程的过程,请认真阅读,并完成相应的任务.
(1)、如图1,当动点P在线段CD上运动时,求证:∠APB=∠CAP+∠DBP;(2)、如图2,当动点P在点C上方运动时(P,A,B不在同一直线上),请写出∠APB,∠CAP,∠DBP之间的数量关系,并选择其中一种的数量关系说明理由.21.(1)、计算:;(2)、下面是小明同学解方程的过程,请认真阅读,并完成相应的任务.解:去分母,得 . 第一步
去括号,得 . 第二步
移项,得 . 第三步
合并同类项.得 . 第四步
系数化为1,得 . 第五步
任务一:①解答过程中,第 ▲ 步开始出现了错误,产生错误的原因是 ▲ ;
②第三步变形的依据是 ▲ .
任务二:①该一元一次方程的解是 ▲ ;
②写出一条解一元一次方程时应注意的事项.
22. 如图,在三角形ABC中, , 将沿射线BC方向平移,得到 , A,B,C的对应点分别是D,E,F,AD∥BF. (1)、请说明;(2)、若 , 当时,求AD的长.
(1)、请说明;(2)、若 , 当时,求AD的长.
-