2024年初中数学人教版七年级下学期期中模拟测试卷 02
试卷更新日期:2024-04-13 类型:期中考试
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 如图, , , 是的平分线,则的度数是( )
 A、50° B、55° C、60° D、65°3. 在平面直角坐标系中,点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列命题是假命题的是( )A、若 , 则 B、若 , , 则 C、三角形的重心是这个三角形的三条角平分线的交点 D、等腰三角形顶角的平分线、底边上的中线、底边上的高相互重合5. 如图,在正方形网格中,每个小正方形的顶点称为格点.点 , 均在格点上,以某一个格点为原点,适当方向为 , 轴的正方向,取相同单位长度建立平面直角坐标系,则下列是同一个坐标系中点 , 的坐标的是( )
A、50° B、55° C、60° D、65°3. 在平面直角坐标系中,点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列命题是假命题的是( )A、若 , 则 B、若 , , 则 C、三角形的重心是这个三角形的三条角平分线的交点 D、等腰三角形顶角的平分线、底边上的中线、底边上的高相互重合5. 如图,在正方形网格中,每个小正方形的顶点称为格点.点 , 均在格点上,以某一个格点为原点,适当方向为 , 轴的正方向,取相同单位长度建立平面直角坐标系,则下列是同一个坐标系中点 , 的坐标的是( ) A、 , B、 , C、 , D、 ,6. 如图,下列能判定∥的条件有几个( )(1)、 (2)(3) (4).
A、 , B、 , C、 , D、 ,6. 如图,下列能判定∥的条件有几个( )(1)、 (2)(3) (4).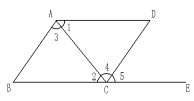 A、4 B、3 C、2 D、17. 如图,平分 , 若 , 则的度数是( )
A、4 B、3 C、2 D、17. 如图,平分 , 若 , 则的度数是( ) A、 B、 C、 D、8. 如图所示,已知数轴上的点A、O、B、C、D分别表示数﹣2、0、1、2、3,则表示数3 的点P应落在( )
A、 B、 C、 D、8. 如图所示,已知数轴上的点A、O、B、C、D分别表示数﹣2、0、1、2、3,则表示数3 的点P应落在( ) A、线段AO上 B、线段OB上 C、线段BC上 D、线段CD上9. 估计的值应在( )A、和之间 B、和 之间 C、和之间 D、和之间10. 如图,在平面直角坐标系中,存在动点P按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2021次运动后,点P的坐标是( )
A、线段AO上 B、线段OB上 C、线段BC上 D、线段CD上9. 估计的值应在( )A、和之间 B、和 之间 C、和之间 D、和之间10. 如图,在平面直角坐标系中,存在动点P按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2021次运动后,点P的坐标是( ) A、(2022,1) B、(2021,0) C、(2021,1) D、(2021,2)
A、(2022,1) B、(2021,0) C、(2021,1) D、(2021,2)二、填空题
-
11. 已知在坐标轴上,则.12. 到x轴距离为6,到y轴距离为4的坐标为 .13. 如图 , , 则、、之间的数量关系是 .
 14. 如图,在四边形中, , , 则度.
14. 如图,在四边形中, , , 则度. 15. 课堂上,老师让同学们从下列数中找一个无理数:其中,甲同学说“”,乙同学说“”,丙同学说“”(1)、甲、乙、丙三位同学中,说错的是.(2)、请将老师所给的数字按要求填入横线内:
15. 课堂上,老师让同学们从下列数中找一个无理数:其中,甲同学说“”,乙同学说“”,丙同学说“”(1)、甲、乙、丙三位同学中,说错的是.(2)、请将老师所给的数字按要求填入横线内:整数:;
负分数:.
16. 如图,已知 , 、分别在、上,点在、之间,连接、 , , 平分 , 平分 , 在的下方有一点 , 平分 , 平分 , 求的度数为 .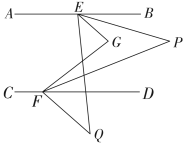
三、解答题
-
17. 已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H.试说明:CD⊥AB.
 18. 如图,直线AB,CD相交于点O,已知、ON将成两个角,且 . 求的度数.
18. 如图,直线AB,CD相交于点O,已知、ON将成两个角,且 . 求的度数. 19. 如图1,直线与直线 , 分别交于点 , , 与互为补角
19. 如图1,直线与直线 , 分别交于点 , , 与互为补角 (1)、请判断直线与的位置关系,并说明理由;(2)、如图2,与的角平分线与交于点 , 延长与交于点 , 过点作垂足为 , 求证:;(3)、在(2)的条件下,连接 , 点是上一点,连接 , 使 , 作的平分线交于点 , 请画出图形.并直接写出的度数.
(1)、请判断直线与的位置关系,并说明理由;(2)、如图2,与的角平分线与交于点 , 延长与交于点 , 过点作垂足为 , 求证:;(3)、在(2)的条件下,连接 , 点是上一点,连接 , 使 , 作的平分线交于点 , 请画出图形.并直接写出的度数.四、实践探究题
-
20. 下面是小李同学探索的近似数的过程:
∵面积为107的正方形边长是 , 且10<<11,
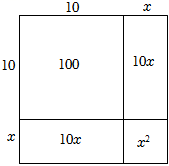
∴设=10+x,其中0<x<1, 画出如图示意图,
∵图中S正方形=102+2×10•x+x2 , S正方形=107
∴102+2×10•x+x2=107
当x2较小时,省略x2 , 得20x+100≈107,得到x≈0.35,即≈10.35.
 (1)、的整数部分是 ;(2)、仿照上述方法,探究的近似值.(画出示意图,标明数据,并写出求解过程)21. 操作探究:已知在纸面上有一数轴(如图所示).
(1)、的整数部分是 ;(2)、仿照上述方法,探究的近似值.(画出示意图,标明数据,并写出求解过程)21. 操作探究:已知在纸面上有一数轴(如图所示). (1)、折叠纸面,使表示1与-1的点重合,则表示-2的点与表示的点重合.(2)、折叠纸面,使表示-1的点与表示3的点重合,回答以下问题.
(1)、折叠纸面,使表示1与-1的点重合,则表示-2的点与表示的点重合.(2)、折叠纸面,使表示-1的点与表示3的点重合,回答以下问题.①表示5的点与表示数的点重合.
②表示的点与表示数的点重合.
③若数轴上A,B两点之间的距离为9(A在B的左侧),且A,B两点经折叠后重合,此时点A表示的数是 , 点B表示的数是
(3)、已知在数轴上点A表示的数是a,将点A移动4个单位长度,此时点A表示的数和a互为相反数,求a的值.五、综合题
-
22. 如图1,直线 , △ABE的顶点E在AB与CD之间.
 (1)、若 , .
(1)、若 , .①当∠CDE=2∠EDM时,求∠BED的度数.
②如图2,作出∠CDE的角平分线DF,当DF平行于△ABE中的一边时,求∠BED的度数.
(2)、如图3,∠CDE的角平分线DF交EB的延长线于点H,连结BF,当∠ABH=2∠HBF,时,求∠CDE的度数.

