2024年初中数学人教版七年级下学期期中模拟测试卷 01
试卷更新日期:2024-04-13 类型:期中考试
一、单选题
-
1. , , , , 3.1416, , 0.101101110…(每两个0之间1的个数依次加1)中,无理数的个数是( )A、1个 B、2个 C、3个 D、4个2. 下列各数中,是无理数的是( )A、 B、π C、 D、03. 直线a,b,c,在同一平面内,下列种说法中,正确的个数为( )
①如果 , , 那么;
②如果 , , 那么;
③如果 , , 那么;
④如果a与b相交,b与c相交,那么a与c相交.
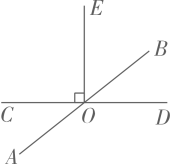
A、1 B、2 C、3 D、44. 如图是路政工程车的工作示意图,工作篮底部与支撑平台平行.若∠1=30°,∠2=50°,则∠3的度数为( ). A、130° B、140° C、150° D、160°5. 下列各点中,在第二象限的点是( )A、 B、 C、 D、6. 下列说法:①有理数与数轴上的点一一对应;②1的平方根是它本身;③立方根是它本身的数是0,1;④对于任意一个实数 , 都可以用表示它的倒数.⑤任何无理数都是无限不循环小数.正确的有( )个.A、0 B、1 C、2 D、37. 如图所示,点在的延长线上,下列条件中能判断的是( )
A、130° B、140° C、150° D、160°5. 下列各点中,在第二象限的点是( )A、 B、 C、 D、6. 下列说法:①有理数与数轴上的点一一对应;②1的平方根是它本身;③立方根是它本身的数是0,1;④对于任意一个实数 , 都可以用表示它的倒数.⑤任何无理数都是无限不循环小数.正确的有( )个.A、0 B、1 C、2 D、37. 如图所示,点在的延长线上,下列条件中能判断的是( )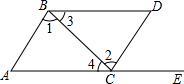 A、 B、 C、 D、8. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度和方向可能是( )A、第一次向左拐50°.第二次向右拐50° B、第一次向左拐50°,第二次向左拐130° C、第一次向右拐50°,第二次向右拐50° D、第一次向右拐50°,第二次向左拐130°9. 过直线l外一点P作直线l的平行线,下列尺规作图中,错误的是( )A、
A、 B、 C、 D、8. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度和方向可能是( )A、第一次向左拐50°.第二次向右拐50° B、第一次向左拐50°,第二次向左拐130° C、第一次向右拐50°,第二次向右拐50° D、第一次向右拐50°,第二次向左拐130°9. 过直线l外一点P作直线l的平行线,下列尺规作图中,错误的是( )A、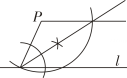 B、
B、 C、
C、 D、
D、 10. 如图,已知 , 下列结论正确的是( )
10. 如图,已知 , 下列结论正确的是( )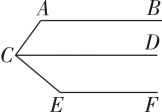 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知∠A与∠B的两边分别平行,其中∠B=(210-2x)°,则x的值为.12. 若无理数满足: , 请写出一个你熟悉的无理数: .13. 如图,已知∠1=65°,∠2=65°,则∥ , 理由是
 14. 如图是对顶角量角器,它所测量的角是度.
14. 如图是对顶角量角器,它所测量的角是度. 15. 如图,已知 , 射线平分交于点 , , 则的度数是 度
15. 如图,已知 , 射线平分交于点 , , 则的度数是 度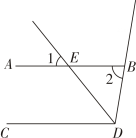 16. 如下图, , 则的度数是
16. 如下图, , 则的度数是
三、解答题
-
17. 已知:如图,直线AB,CD被直线EF所截,EG平分∠AEF,FG平分∠CFE,∠1+∠2=90°.求证:AB∥CD.
 18. 如图,AB⊥AC,点D、E分别在线段AC、BF上,DF、CE分别与AB交于点M、N,若∠1=∠2,∠C=∠F,求证;AB⊥BF.请完善解答过程,并在括号内填写相应的依据.
18. 如图,AB⊥AC,点D、E分别在线段AC、BF上,DF、CE分别与AB交于点M、N,若∠1=∠2,∠C=∠F,求证;AB⊥BF.请完善解答过程,并在括号内填写相应的依据.
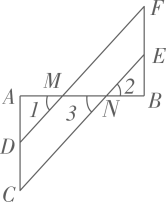
证明:∵∠1=∠2,∠2=∠3,
∴∠1=∠ ▲ . (等量代换)
∴DF∥CE( )
∴∠ADM=∠ ▲ (两直线平行,同位角相等)
∵∠C=∠F,(已知)
∴∠ADM=∠ ▲ (等量代换)
∴AC∥BF( )
∴∠A=∠B( )
∵AB⊥AC,(已知)
∴∠A=90°.
∴∠B=90°.
∴AB⊥BF.( )
19. 已知直线 , 一块含角的直角三角板 , 顶点在直线上. (1)、如图 , 若 , 求的度数;(2)、如图 , 向上平移直线 , 使直线过点 , , , 若是的倍,求证: .
(1)、如图 , 若 , 求的度数;(2)、如图 , 向上平移直线 , 使直线过点 , , , 若是的倍,求证: .四、实践探究题
-
20. 【教材呈现】如图是华师版七年级上册数学教材第176页的部分内容.有了“两直线平行,同位角相等”,我们就能用推理的方法得出“两条平行线被第三条直线所截,内错角相等”.

如图①,已知平行线a、b被直线l所截,我们将∠1的对顶角记为∠3.
(1)、下面是“两直线平行,内错角相等”的推理过程,在括号内填写理由.∵a∥b( ),
∴∠2=∠3( ).
∵∠1=∠3( ),
∴∠1=∠2( ).
(2)、【拓展应用】如图②,AB∥CD,BC∥DE,若∠B=47°,则∠D=°.(3)、如图③,已知AB∥CD,∠1=∠2,试说明∠BEF=∠EFC.21. 阅读与思考阅读下面的文字,并完成相应的任务.
大家知道是无理数,而无理无限不循环小数,因此的小数部分我们不可能全部写出来,我们可以减去它的整数部分就可以得到小数部分,于是我们需要先对这个数进行估值.因为 , 即 , 所以的整数部分为2,小教部分为.
任务:已知a是的整数部分,b是的小数部分.
(1)、求a,b的值.(2)、求的算术平方根.五、综合题
-
22. 如图,直线 , 直线与 , 分别交于点 , , .小安将一个含角的直角三角板按如图①放置,使点、分别在直线、上,且在点、的右侧, , .


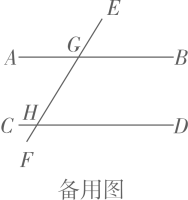 (1)、填空; (填“”“ ”或“=” );(2)、若的平分线交直线于点 , 如图②.
(1)、填空; (填“”“ ”或“=” );(2)、若的平分线交直线于点 , 如图②.①当 , 时,求的度数;
②小安将三角板沿直线左右移动,保持 , 点、分别在直线和直线上移动,请直接写出的度数(用含的式子表示).