湘教版2023-2024学年初中数学七年级下学期期中模拟测试卷 03
试卷更新日期:2024-04-13 类型:期中考试
一、单选题
-
1. 计算m2•m3的结果是( )A、m6 B、m5 C、m8 D、m92. 下列计算中,正确的是( )A、 B、 C、 D、3. 下列各式从左边到右边的变形中,属于因式分解的是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,绳长、井深各几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,绳长、井深各几尺?若设绳长为x尺,井深为y尺,则符合题意的方程组是( )A、 B、 C、 D、6. 把代数式x2﹣4x+4分解因式,下列结果中正确的是( )A、(x﹣2)2 B、(x+2)2 C、x(x﹣4)+4 D、(x﹣2)(x+2)7. 下列方程中.属于二元一次方程的是( )A、 B、 C、 D、8. 有两个正方形A,B.现将B放在A的内部得图甲,将A,B构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,若三个正方形A和两个正方形B得图丙,则阴影部分的面积为( )
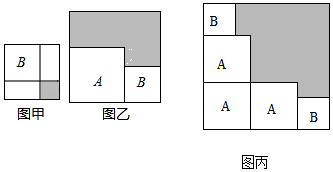 A、28 B、29 C、30 D、31
A、28 B、29 C、30 D、31二、填空题
-
9. 计算的结果等于 .10. 计算: .11. 若x3•(xn)5=x18 , 则n= .12. “今有四十鹿进舍,小舍容四鹿,大舍容六鹿,需舍几何?(改编自《缉古算经》)”大意为.今有50只鹿进圈舍,小圈舍可以容纳4头鹿,大圈舍可以容纳6头鹿,且恰好每个圈舍都能放满,求所需圈舍的间数.设所需大圈舍x间,小圈舍y间,则x+y求得的结果有 种.13. 计算 的结果是 .14. 无论a取何值,关于x、y的二元一次方程(2a-1)x+(a+2)y+5-2a=0总有一个公共解,这个公共解是.15. 设m =(2+1)(22+1)(24+1)…(264+1),则m的个位数字是.16. 某运输公司有核定载重量之比为 的甲、乙、丙三种货车,该运输公司接到为某灾区免费运输物资任务,迅速按照各车型核定载重量将物资运往灾区,承担本次运输的三种货车数量相同,当这批物资送达灾区后,发现还需要一部分物资才能满足当地灾区的需要,于是该运输公司又安排部分甲、乙丙三种货车进行第二次运输,其中乙型车第二次送输的物资量是还需要运输的物资量的 ,丙型车两次运输的物资总量是两次运往灾区物资总量的 ,甲型车两次运输的物资总量与乙型车两次运输的物总量之比为 ,则甲型车第一次与甲型车第二次运输的物资量之比是.
三、解答题
-
17. 某班同学与幼儿园小朋友联谊,带去一筐苹果.分苹果时发现,如果每人分 6个,那么还缺6个;如果每人分5个,那么多出5个.问有多少个小朋友?有多少个苹果?18. 小王同学在学习完全平方公式时,发现这四个代数式之间是有联系的,他在研究后提出了以下三个问题:

请帮他解决这三个问题.(1)、已知 , 求ab的值.(2)、已知求的值.(3)、如图,长方形ABCD中,AB=6cm,BC=8cm,正方形AEHG,EBKF和NKCM都在它的内部,且BK>KC.记AE=a(cm),CM=b(cm),若a2+b2=18cm2 , 求长方形PFQD的面积.19. 列方程组解应用题.某工厂生产的甲、乙两种产品均需加入同种添加剂,甲产品每箱需加该添加剂2克,乙产品每箱需加该添加剂3克,已知270克该添加剂恰好生产了甲、乙两种产品共100箱,问甲、乙两种产品各生产多少箱.四、实践探究题
-
20. 将完全平方公式(a±b)2=a2±2ab+b2进行适当的变形,可以解决很多的数学问题,例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,所以(a+b)2=9,即a2+2ab+b2=9.
又因为ab=1,所以a2 +b2=7.
根据上面的解题思路与方法,解决下列问题:
(1)、若x+y=8,x2+y2=40,则xy=;(2)、若x-y=6,xy=5,求x2+y2的值;(3)、两个正方形ABCD、AEFG如图摆放,面积和为34,BG=8,则图中阴影部分面积和为
五、综合题
-
21. 检验下列因式分解是否正确.(1)、 ;(2)、 ;(3)、 ;(4)、 .22. ((教材呈现)下图是华师版八年级上册数学教材第49页B组的第12题和第13题.
 已知 ,求 的值.
已知 ,求 的值.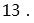 已知 ,求 的值.
已知 ,求 的值.
(例题讲解)老师讲解了第12题的两种方法:
方法一
方法二
∵ ,
∴ .
∴ .
∵ ,
∴ .
∵
∴ .
∵ ,
∴ .
(1)、(方法运用)请你任选第12题的解法之一,解答教材第49页B组的第13题.(2)、(拓展)如图,在 中, ,分别以 、 为边向其外部作正方形 和正方形 .若 ,正方形 和正方形 的面积和为18,求 的面积.23. 图1是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形. (1)、观察图2,请你写出下列三个代数式(a+b)2 , (a﹣b)2 , ab之间的等量关系为 .(2)、运用你所得到的公式,计算:若m、n为实数,且mn=﹣3,m﹣n=4,试求m+n的值.(3)、如图3,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=26,求图中阴影部分面积.
(1)、观察图2,请你写出下列三个代数式(a+b)2 , (a﹣b)2 , ab之间的等量关系为 .(2)、运用你所得到的公式,计算:若m、n为实数,且mn=﹣3,m﹣n=4,试求m+n的值.(3)、如图3,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=26,求图中阴影部分面积.
-