湘教版2023-2024学年初中数学七年级下学期期中模拟测试卷 02

试卷更新日期：2024-04-13 类型：期中考试

进入出卷网下载

一、单选题

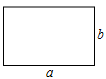
1. 下列运算正确的是（）

A、 $a^{3} \cdot a^{2} = a^{5}$ B、 ${(a^{2})}^{3} = a^{5}$ C、 ${(a b)}^{2} = a b^{2}$ D、 $a^{3} + a^{2} = a^{5}$

查看试题解析
2. 计算 $(- 2)^{101} \times {(\frac{1}{2})}^{100}$ 的结果是（）

A、 $- 1$ B、 $1$ C、 $2$ D、 $- 2$

查看试题解析
3. 方程组 $\frac{x}{3} = \frac{y}{2} = x + y - 4$ 的解为（）

A、 $\{\begin{matrix} x = - 3 ， \\ y = - 2 \end{matrix}$ B、 $\{\begin{matrix} x = 6 ， \\ y = 4 \end{matrix}$ C、 $\{\begin{matrix} x = 2 ， \\ y = 3 \end{matrix}$ D、 $\{\begin{matrix} x = 3 ， \\ y = 2 \end{matrix}$

查看试题解析
4. 若x²+kx+9是一个完全平方式，则常数 $k$ 的值为（）

A、6 B、-6 C、 $\pm 6$ D、无法确定

查看试题解析
5. 下列分解因式正确的是（）

A、a²+a+1=a（a+1）+1 B、a²-ab=a（a-1） C、a²-4b²=（a+2b）（a-2b） D、a²+2ab+b²=（a-b）²

查看试题解析
6. 《九章算术》是中国古代重要的数学著作，其中有这样一道题：“今有醇酒一斗，直钱五十；行酒一斗，直钱一十.今将钱三十，得酒二斗，问醇、行酒各得几何?”译文：今有醇酒（优质酒）1斗，价格50钱；行酒（勾兑酒）1斗，价格10钱.现有30钱，买2斗酒，问能买醇、行酒各多少斗?设能买醇酒x斗，行酒y斗，可列二元一次方程组为（）

A、 ${\begin{array}{l} x + y = 2 \\ 10 x + 50 y = 20 \end{array}$ B、 ${\begin{array}{l} x + y = 2 \\ 30 x + 10 y = 50 \end{array}$ C、 ${\begin{array}{l} x + y = 2 \\ 50 x + 10 y = 30 \end{array}$ D、 ${\begin{array}{l} x + y = 2 \\ 10 x + 30 y = 50 \end{array}$

查看试题解析
7. 如图，在一块长 $15 m$ ，宽 $12 m$ 的长方形空地上，修建同样宽的两条互相垂直的道路 $($ 两条道路各与长方形的一条边垂直 $)$ ，剩余部分栽种花草美化环境，设道路的宽度为 $x m$ ，则栽种花草的面积表示不正确的是（）

A、 $(15 - x) (12 - x)$ B、 $15 \times 12 - 15 x - 12 x + x^{2}$ C、 $15 \times 12 - x (15 - x) - x (12 - x) - x^{2}$ D、 $(15 - x) (12 - x) + x^{2}$

查看试题解析
8. 若方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解是 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ ，则方程组 ${\begin{array}{l} 3 a_{1} x + 2 b_{1} y = a_{1} + c_{1} \\ 3 a_{2} x + 2 b_{2} y = a_{2} + c_{2} \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = \frac{4}{3} \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = \frac{4}{3} \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = - 1 \\ y = - 1 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = 1 \end{array}$

查看试题解析
9. 下列各式中，计算结果为 $a^{12}$ 的是（）

A、 ${(- a^{4})}^{8}$ B、 $(- a^{4}) \cdot a^{8}$ C、 $a^{3} \cdot {(- a)}^{6}$ D、 ${(- a^{3})}^{4}$

查看试题解析
10. 数形结合是数学解题中常用的思想方法，数形结合的思想可以使某些抽象的数学间题直观化、生动化，能够变抽象思维为形象思维，有助于把握数学问题的本质在学习整式运算乘法公式的过程中，每个公式的推导教材都安排了运用图形面积来加以验证．现有下图中甲、乙两种方案，能借助图形面积验证（a＋b）（a－b）＝a²－b²的正确性方案的是（）

A、只有甲能 B、只有乙能 C、甲、乙都不能 D、甲、乙都能

查看试题解析

二、填空题

11. 计算： $(2 a^{2} b^{3})^{2} =$ ．

查看试题解析
12. 几个人一起买物品，若每人出8元，则盈余3元；若每人出7元，则还差4元，则此物品的价格是．

查看试题解析
13. 已知 ${\begin{array}{l} x = 1 \\ y = - 2 \end{array}$ 是方程 $k x - y = 3$ 的一个解，那么k的值是；

查看试题解析
14. 对 $x ， y$ 定义一种新运算“&amp；”，规定： $x & y = m x + n y$ （其中 $m ， n$ 均为非零常数）， $1 & 1 = 3 ， 1 & 2 = 5$ .则 $2 & (- 1)$ 的值是.

查看试题解析
15. 下图中的四边形均为长方形，根据图形的面积关系，写出一个正确的等式：．

查看试题解析
16. 二元一次方程组 $\{\begin{matrix} 2 x + 3 y = 2 k + 3 ① \\ 3 x + 2 y = k - 2 ② \end{matrix}$ 的解满足x+y=2，则k的值为

查看试题解析
17. 有一个正方形的花园，如果它的边长增加 $2 m$ ，那么花园面积将增加 $16 m^{2}$ ，则原花园的面积为．

查看试题解析
18. $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \dots (1 - \frac{1}{99^{2}}) (1 - \frac{1}{100^{2}})$ =；

查看试题解析

三、解答题

19. 某网店用24000元的资金购进A、B两种玩具共700件，准备在“双十一”期间销售，A、B两种玩具的进价分别为60元、15元：

(1)、网店本次购进A、B两种玩具的数量分别是多少？

(2)、该网店的A种玩具在“双十一”期间销售火爆，商家决定向厂家再次追加A种玩具，厂家接到定单后，马上安排车间的68名工人加班生产A种玩具．一个A种玩具是由2个甲种配件和3个乙种配件组成的，每名工人每天可生产甲种配件16个或乙种配件10个，那么需要分别安排多少名工人加工甲、乙两种配件，才能使每天加工的甲、乙两种配件刚好配套？

查看试题解析
20. 已知实数m，n满足 $m + n = 6$ ， $m n = - 3$ ．

(1)、求 $(m + 2) (n + 2)$ 的值；

(2)、求 $m^{2} + n^{2}$ 的值．

查看试题解析
21. 已知关于x，y的二元一次方程组 $\{\begin{matrix} 2 x + y - 6 = 0 ， \\ 2 x - 2 y + m y + 8 = 0 . \end{matrix}$

(1)、请直接写出方程2x+y-6=0的所有正整数解.

(2)、若方程组的解满足x-y=0，求m的值.

(3)、若方程组无解，求m的值.

(4)、无论实数m取何值，方程2x-2y+my+8=0总有一个固定的解，请求出这个解.

查看试题解析

四、实践探究题

22. 阅读材料：
分解因式 ${(a + b)}^{2} + 2 (a + b) + 1 .$
解：设 a+b=x，则原式 $= x^{2} + 2 x + 1 = (x + 1)^{2} =$ ${(a + b + 1)}^{2} .$
这样的解题方法叫做“换元法”，即当复杂的多项式中，某一部分重复出现时，我们用字母将其替换，从而简化这个多项式.
“换元法”是一种重要的数学方法，不少问题能用“换元法”解决.
请用“换元法”对下列多项式进行因式分解：

(1)、 ${(m + n)}^{2} - 18 (m + n) + 81 .$

(2)、 $(x^{2} - 4 x + 2) (x^{2} - 4 x + 6) + 4 ，$

查看试题解析
23. 【方法体验】已知方程组 ${\begin{array}{l} 2018 x - 2017 y = 20 ， & ① \\ 2019 x + 2018 y = 500 ． & ② \end{array}$ 求4037x+y的值.小明同学发现解此方程组代入求值很麻烦!后来他将两个方程直接相加便迅速解决了问题.请你体验一下这种快捷思路，写出具体解题过程：
【方法迁移】根据上面的体验，填空：
已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 10 \\ 4 x + 3 y + 2 z = 15 \end{array}$ ，则3x+y–z=      ▲      .
【探究升级】已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 10 \\ 4 x + 3 y + 2 z = 15 \end{array}$ .求–2x+y+4z的值.小明凑出“–2x+y+4z=2•（x+2y+3z）+（–1）•（4x+3y+2z）=20–15=5”，虽然问题获得解决，但他觉得凑数字很辛苦!他问数学老师丁老师有没有不用凑数字的方法，丁老师提示道：假设–2x+y+4z=m•（x+2y+3z）+n•（4x+3y+2z），对照方程两边各项的系数可列出方程组 ${\begin{array}{l} m + 4 n = - 2 \\ 2 m + 3 n = 1 \\ 3 m + 2 n = 4 \end{array}$ ，它的解就是你凑的数!
根据丁老师的提示，填空：2x+5y+8z=      ▲      （x+2y+3z）+      ▲      （4x+3y+2z）.
【巩固运用】已知2a–b+kc=4，且a+3b+2c=–2，当k为      ▲      时，8a+3b–2c为定值，此定值是      ▲      .（直接写出结果）

查看试题解析

五、综合题

24. 公元3世纪，古希腊数学家丢番图（Diophantus）在其《算术》一书中设置了以下问题：已知两正整数之和为20，乘积为96，求这两个数．因为两数之和为20，所以这两个数不可能同时大于10，也不可能同时小于10，必定是一个大于10，一个小于10．根据如图所示的设法，可设一个数为 $10 + x$ ，则另一个数为 $10 - x$ ，根据两数之积为96，可得 $(10 + x) (10 - x) = 96$ ．请根据以上思路解决下列问题：

(1)、若两个正整数之和为100，大数比小数大 $2 a$ ，根据丢番图的设法，这两个正整数可表示为和；

(2)、请你根据丢番图的运算方法，计算 $502 \times 498$ 的值．

查看试题解析
25. 灵活运用完全平方公式 ${(a \pm b)}^{2} = a^{2} \pm 2 a b + b^{2}$ 可以解决许多数学问题．
例如：已知 $a - b = 3 ， a b = 1$ ，求 $a^{2} + b^{2}$ 的值．
解： $∵ a - b = 3 ， a b = 1$ ， ∴ ${(a - b)}^{2} = 9 ， 2 a b = 2 ， ∴ a^{2} - 2 a b + b^{2} = 9$ ，
$∴ a^{2} - 2 + b^{2} = 9 ， ∴ a^{2} + b^{2} = 9 + 2 = 11$ ．
请根据以上材料，解答下列问题．

(1)、若 $a^{2} + b^{2}$ 与 $2 a b - 4$ 互为相反数，求 $a + b$ 的值．

(2)、如图，矩形的长为a，宽为b，周长为14，面积为8，求 $a^{2} + b^{2}$ 的值．

查看试题解析