湘教版2023-2024学年初中数学七年级下学期期中模拟测试卷 01
试卷更新日期:2024-04-13 类型:期中考试
一、单选题
-
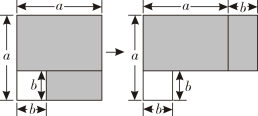
1. 下列计算正确的是( )A、 B、 C、 D、2. 如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,再将剩下的阴影部分剪开,拼成右边的长方形.根据图形的变化过程可以验证下列哪一个等式成立?( )
 A、 B、 C、 D、3. 已知是方程的解,a,b是正整数,则的最大值是( )A、8 B、6 C、4 D、34. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 二元一次方程2x﹣y=3的解可以是( )A、 B、 C、 D、7. 下列各多项式中,能运用公式法分解因式的有( )A、 B、 C、 D、8. 用若干个形状,大小完全相同的长方形纸片围成正方形,个长方形纸片围成如图所示的正方形,其阴影部分的面积为;个长方形纸片围成如图所示的正方形,其阴影部分的面积为;个长方形纸片围成如图所示的正方形,其阴影部分的面积为 ( )
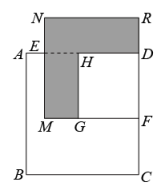
A、 B、 C、 D、3. 已知是方程的解,a,b是正整数,则的最大值是( )A、8 B、6 C、4 D、34. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间客房.设该店有客房x间、房客y人,下列方程组中正确的是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 二元一次方程2x﹣y=3的解可以是( )A、 B、 C、 D、7. 下列各多项式中,能运用公式法分解因式的有( )A、 B、 C、 D、8. 用若干个形状,大小完全相同的长方形纸片围成正方形,个长方形纸片围成如图所示的正方形,其阴影部分的面积为;个长方形纸片围成如图所示的正方形,其阴影部分的面积为;个长方形纸片围成如图所示的正方形,其阴影部分的面积为 ( ) A、 B、 C、 D、9. 若 , 则( )A、3 B、6 C、 D、10. 如图,在长方形中, , 其内部有边长为a的正方形与边长为b的正方形 , 两个正方形的重合部分也为正方形,且面积为5,若 , 则正方形与正方形的面积之和为( )
A、 B、 C、 D、9. 若 , 则( )A、3 B、6 C、 D、10. 如图,在长方形中, , 其内部有边长为a的正方形与边长为b的正方形 , 两个正方形的重合部分也为正方形,且面积为5,若 , 则正方形与正方形的面积之和为( ) A、29 B、25 C、 D、
A、29 B、25 C、 D、二、填空题
-
11. 计算: .12. 若 , , 则 .13. 因式分解: =.14. 若且则 .15. 若方程组的解x,y满足 , 则的取值范围为 .16. 一个四位数n , 如果千位与十位上的数字之和等于百位与个位上的数字之和,则称n为“等和数”,将这个“等和数”反序排列(即千位与个位对调,百位与十位对调)得到一个新的四位数m , 记 , 则D(1254)=;若某个“等和数”n的千位与十位上的数字之和为8,D(n)为正数且能表示为两个连续偶数的平方差,则满足条件的最大“等和数”n是 .
三、解答题
-
17. 化简:(3m-4n)(3m+4n) (9m2+16n2 ).18. 列方程组解应用题:
端午期间某超市销售价格相同的粽子与咸鸭蛋的组合礼品盒,甲种礼品每盒含12只粽子和4枚咸鸭蛋,售价72元;乙种礼品每盒含10只粽子和8枚咸鸭蛋,售价74元(礼品盒的价格忽略不计),问一只粽子和一枚咸鸭蛋各多少元?
19. 如图①是一个长为 , 宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形,请解答下列问题: (1)、图②中阴影部分的正方形的边长是;(2)、用两种不同的方法求图②中阴影部分的面积:
(1)、图②中阴影部分的正方形的边长是;(2)、用两种不同的方法求图②中阴影部分的面积:方法1: ▲ ;
方法2: ▲ ;
并写出二个代数式之间的等量关系;
(3)、根据(2)中的等量关系,解决问题:若 , 求的值;(4)、根据(2)中的等量关系,直接写出和之间的关系;若 , 分别求出和的值;(5)、【知识迁移】类似地,用两种不同的方法计算同一几何体的体积 , 也可以得到一个恒等式.根据图③,写出一个代数怛等式:;(6)、已知 , 利用上面的规律求的值.四、实践探究题
-
20. 阅读材料:下面是底数大于1的数比较大小的两种方法:
①比较 , 的大小:当时, , 所以当同底数时,指数越大,值越大;
②比较和的大小:因为 , , 所以 .
可以将其先化为同指数,再比较大小,所以同指数时,底数越大,值越大.
根据上述材料,解答下列问题:
(1)、比较大小:(填“”或“”)(2)、已知 , , , 试比较 , , 的大小.21. 根据几何图形的面积关系可以说明数学等式,例如:(2a+b)(a+b)=2a2+3ab+b2 , 可以用图①的面积关系来说明,由此我们识可以得到(2a+b)(a+b)-(2a2+b2)=3ab. (1)、根据图②的面积关系可得:(2a+b)(a+2b)-(2a2+2b2)=;(2)、有若干张如图③的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a,宽为b的长方形.并用这些纸片无缝隙无重叠地拼成了图④,图⑤,图⑥的图形,图④,图⑤,图⑥中的阴影部分面积分别记为S1 , S2 , S3;
(1)、根据图②的面积关系可得:(2a+b)(a+2b)-(2a2+2b2)=;(2)、有若干张如图③的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a,宽为b的长方形.并用这些纸片无缝隙无重叠地拼成了图④,图⑤,图⑥的图形,图④,图⑤,图⑥中的阴影部分面积分别记为S1 , S2 , S3;
①S1= ▲ , S2= ▲ , S3= ▲ (用含a, b的代数式表示);
②若3S2-S1=108,S3=9,求图⑥中大正方形的面积.
22. 对于未知数为 , 的二元一次方程组,如果方程组的解 , 满足 , 我们就说方程组的解与具有“邻好关系”.(1)、方程组的解与 项“具有”或“不具有”“邻好关系”;(2)、若方程组的解与具有“邻好关系”,求的值;(3)、未知数为 , 的方程组 , 其中与 , 都是正整数,该方程组的解与是否具有“邻好关系”?如果具有,请求出的值及方程组的解;如果不具有,请说明理由.(4)、【拓展】若一个关于的方程的解为 , 则称之为“成章方程”如:的解为 , 而;的解为 , 而.请直接写出关于的“成章方程”的解:.
若关于的方程为“成章方程”,请直接写出关于的方程的解:.
五、综合题
-
23. 已知某物流公司租用2辆A型车和1辆B型车载满货物一次可运货10吨;租用1辆A型车和2辆B型车载满货物一次可运货11吨.该物流公司现有26吨货物,计划A型车a辆,B型车b辆,每辆车都载满货物,且恰好一次运完.(1)、问租用1辆A型车和1辆B型车都载满货物一次可分别运货多少吨?(2)、为完成运输任务,且同时租用A型与B型两种车辆,请你帮该物流公司设计租车方案.(3)、若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请写出最省钱的租车方案,并求出最少租车费.