2024年北师大版数学七(下)重难点培优训练5 平行线的判定与性质综合
试卷更新日期:2024-04-13 类型:复习试卷
一、选择题
-
1. 如图, , 与的角平分线交于点G,且 , 已知 , 若 , , 则下列等式中成立的是( )
 A、 B、 C、 D、2. 如图,已知 , 若按图中规律继续划分下去,则等于( )
A、 B、 C、 D、2. 如图,已知 , 若按图中规律继续划分下去,则等于( ) A、 B、 C、 D、3. 已知 , 点E在连线的右侧,与的角平分线相交于点F,则下列说法正确的是( );
A、 B、 C、 D、3. 已知 , 点E在连线的右侧,与的角平分线相交于点F,则下列说法正确的是( );①;
②若 , 则;
③如图(2)中,若 , , 则;
④如图(2)中,若 , , 则.
 A、①②④ B、②③④ C、①②③ D、①②③④4. 为了亮化某景点,石家庄市在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转,B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动30°,B灯每秒转动10°,B灯先转动2秒,A灯才开始转动,当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是( )
A、①②④ B、②③④ C、①②③ D、①②③④4. 为了亮化某景点,石家庄市在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转,B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动30°,B灯每秒转动10°,B灯先转动2秒,A灯才开始转动,当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是( ) A、1或6秒 B、8.5秒 C、1或8.5秒 D、2或6秒5. ①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )
A、1或6秒 B、8.5秒 C、1或8.5秒 D、2或6秒5. ①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )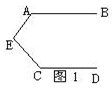


 A、、1个 B、2个 C、3个 D、4个
A、、1个 B、2个 C、3个 D、4个二、填空题
-
6. 一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动(旋转角不超过180度),使两块三角尺至少有一组边互相平行.如图2:当∠BAD=15°时,BC∥DE.则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为
 7. 如图1是一张长方形纸带,∠DEF=20°,若将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中的∠CFE的度数为°.
7. 如图1是一张长方形纸带,∠DEF=20°,若将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中的∠CFE的度数为°. 8. 如图,直线 , 点E、F分别为直线和上的点,点P为两条平行线间的一点,连接和 , 过点P作的平分线交直线于点G,过点F作 , 垂足为H,若 , 则°.
8. 如图,直线 , 点E、F分别为直线和上的点,点P为两条平行线间的一点,连接和 , 过点P作的平分线交直线于点G,过点F作 , 垂足为H,若 , 则°.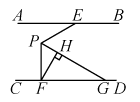 9. 如图,已知长方形纸片 , 点和点分别在边和上,且 , 点和点分别是边和上的动点,现将点 , , , 分别沿 , 折叠至点 , , , , 若 , 则的度数为 .
9. 如图,已知长方形纸片 , 点和点分别在边和上,且 , 点和点分别是边和上的动点,现将点 , , , 分别沿 , 折叠至点 , , , , 若 , 则的度数为 . 10. 如图,直线 , 则的度数为°.
10. 如图,直线 , 则的度数为°.
三、实践探究题
-
11.
 (1)、【问题探究】如图1, , , , 求的度数.(2)、【思维迁移】如图2, , 若点P在B,D两点之间运动,记 , , 问与α,β之间有何数量关系?请写出解题过程.(3)、【拓展延伸】如图3, , 在射线上,若点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),记 , , 请直接写出与α,β之间的数量关系.12. [阅读材料]欢欢:老师说在解决有关平行线的问题时,如果无法直接得到角的关系,就需要借助辅助线来帮助解答.例:
(1)、【问题探究】如图1, , , , 求的度数.(2)、【思维迁移】如图2, , 若点P在B,D两点之间运动,记 , , 问与α,β之间有何数量关系?请写出解题过程.(3)、【拓展延伸】如图3, , 在射线上,若点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),记 , , 请直接写出与α,β之间的数量关系.12. [阅读材料]欢欢:老师说在解决有关平行线的问题时,如果无法直接得到角的关系,就需要借助辅助线来帮助解答.例:已知:如图1, , 为 , 之间的点,连接 , 得到 .
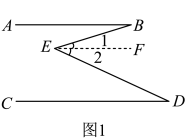
求证: .
证明:如图1,过点作 , ∴ .
∵ , , ∴ ▲ .
∴ .
∵ , ∴ .
[问题解答]
(1)、请补全材料中的推理过程;(2)、请利用材料中得到的结论或解题方法,完成下面的问题:①如图2, , , 求的度数;

②如图3, , 分别交的两边于点 , , , , 点在射线上, , , 那么当点在 , 两点之间移动时,与 , 之间有何数量关系?请说明理由.
 13. 阅读资料:在学习平行线知识的时候,小敏同学发现有的图形(如图1),不属于两条平行线被第三条直线所截的图形,不能直接应用平行线的性质解决问题.经过思考,小敏想到,若过点C作CF∥AB(如图2),这样就多了一个已知条件,问题就可以解决了.
13. 阅读资料:在学习平行线知识的时候,小敏同学发现有的图形(如图1),不属于两条平行线被第三条直线所截的图形,不能直接应用平行线的性质解决问题.经过思考,小敏想到,若过点C作CF∥AB(如图2),这样就多了一个已知条件,问题就可以解决了.
请你参考小敏同学的方法,解决下面问题:
(1)、如图2,已知AB∥DE,用等式表示∠B,∠E,∠BCE之间的数量关系,并说明理由.(2)、如图3,已知AB∥DE,直接用等式表示出∠B,∠E,∠BCE之间的数量关系.14. 探究题:背景材料:如图①,若 , 则
理由:过作 , 因为 , 所以,(如果两条直线都与第三条直线平行,那么这两条直线也互相平行)
由 , 得 , 由 , 得 . (两直线平行,内错角相等)
由 , 所以, , (等量代换).
 (1)、希望小组的同学发现,图①中若 , 可得出 . 请说明理由;(2)、雄鹰小组的同学将点移至图②的位置,此时 , , 之间也存在着一种数量关系?请直接写出结论;(3)、勤奋小组的同学将点移至图③的位置,此时 , , 之间的关系又如何?请写出结论并说明理由;(4)、创新小组的同学画出了图④,若 , 与之间有数量关系?请直接写出结论.15. 综合与实践
(1)、希望小组的同学发现,图①中若 , 可得出 . 请说明理由;(2)、雄鹰小组的同学将点移至图②的位置,此时 , , 之间也存在着一种数量关系?请直接写出结论;(3)、勤奋小组的同学将点移至图③的位置,此时 , , 之间的关系又如何?请写出结论并说明理由;(4)、创新小组的同学画出了图④,若 , 与之间有数量关系?请直接写出结论.15. 综合与实践【问题情境】
在综合与实践课上,同学们以“一个含的直角三角尺和两条平行线”为背景开展数学活动.如图1,已知两直线a,b且和 , , , .
 (1)、在图1中, , 求的度数;(2)、 【深入探究】
(1)、在图1中, , 求的度数;(2)、 【深入探究】如图2,创新小组的同学把直线a向上平移,并把的位置改变,发现 , 请说明理由;
(3)、 【拓展应用】缜密小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,平分 , 此时发现与又存在新的数量关系,请直接写出与的数量关系.
16. (1)、【感知】如图①, , , , 的度数为 .(2)、【探究】如图②, , 点P在射线上运动, , ,
(1)、【感知】如图①, , , , 的度数为 .(2)、【探究】如图②, , 点P在射线上运动, , ,①当点P在线段上运动时,试探究 , , 之间的数量关系.
②当点P在线段C,D两点外侧运动时(点P与点C,D,O三点不重合),直接写出 , , 之间的数量关系为 .
17. 如图, , 定点E,F分别在直线上,在平行线之间有一动点P,满足 . (1)、试问满足怎样的数量关系?
(1)、试问满足怎样的数量关系?解:由于点P是平行线之间有一动点,因此需要对点P的位置进行分类讨论:
如图1,当P点在的左侧时,满足数量关系为 ,
如图2,当P点在的右侧时,满足数量关系为 .
(2)、如图3,分别平分和 , 且点P在左侧.①若 , 则 .
②猜想与的数量关系,并说明理由;
③如图4,若与的角平分线交于点 , 与的角平分线交于点 , 与的角平分线交于点;此次类推,则与满足怎样的数量关系?(直接写出结果)
(3)、【拓展应用】如图5,已知 , 点E在直线上,点P在直线上方,连接 , 的角平分线与的角平分线所在直线交于点Q,则= °. 18.
18.
【阅读理解】:两条平行线间的拐点问题经常可以通过作一条直线的平行线进行转化.
例如:如图1, , 点、分别在直线、上,点在直线、之间.问 , , 之间有何数量关系?请说明理由.
小铭同学发现 , 并给出了部分理由.
如图 , 过点作 ,
因为 , ,
所以 ,
…;
(1)、请将上面的说理过程补充完整;(2)、如图2,若 , ∠ , . 则 ;(3)、 【方法运用】如图3, , 点在的上方,问 , , 之间有何数量关系?请说明理由;
(4)、 【联想拓展】如图4,已知 , 的平分线和的平分线交于点 , 请你用含有的式子表示的度数,直接写出结果.
19. 【阅读材料】在“相交线与平行线”的学习中,有这样一道典型问题:
如图①,AB∥CD,点P在AB与CD之间,可得结论:∠BAP+∠APC+∠PCD=360°.

理由如下:
过点P作PQ∥AB.
∴∠BAP+∠APQ=180°.
∵AB∥CD,
∴PQ∥CD.
∴∠PCD+∠CPQ=180°.
∴∠BAP+∠APC+∠PCD
=∠BAP+∠APQ+∠CPQ+∠PCD
=180°+180°
=360°.

【问题解决】
(1)、如图②,AB∥CD,点P在AB与CD之间,写出∠BAP,∠APC,∠PCD间的等量关系;(只写结论)(2)、如图③,AB∥CD,点P,E在AB与CD之间,AE平分∠BAP,CE平分∠DCP.写出∠AEC与∠APC间的等量关系,并说明理由;(3)、如图④,AB∥CD,点P,E在AB与CD之间,∠BAE=∠BAP,∠DCE=∠DCP,写出∠AEC与∠APC间的等量关系.(只写结论)20. 综合与实践【问题情境】
在一次综合与实践课上,老师让同学们以平行线为主题,进行相关问题的探究,进一步感受平行线在寻找角之间的关系的作用,以下是智慧小组的活动过程,请你加入他们小组一起完成探究.
(1)、【初步探究】如图, , 当 , 时,试求∠2的大小;
 (2)、【深入探究】
(2)、【深入探究】经过探究发现,图1中的∠1,∠2,∠3之间存在着一定的数量关系,下列选项中能正确表示这种关系的是____;
A、 B、 C、 D、(3)、【拓展应用】如图,一条公路经过三次拐弯后又回到原来的方向,若第一次的拐角第三次的拐角 , 则第二次的拐角 .
 21.(1)、【问题情景】如图 , , , , 求的度数;
21.(1)、【问题情景】如图 , , , , 求的度数; (2)、【问题迁移】如图 , 已知 , ADBC,点在射线上运动,当点在 , 两点之间运动时,连接 , , , , 求与 , 之间的数量关系,并说明理由;(3)、【知识拓展】在(2)的条件下,若将“点在 , 两点之间运动”改为“点在 , 两点外侧运动点与点 , , 三点不重合”其他条件不变,请直接写出与 , 之间的数量关系.22. 【阅读思考】单元复习课后,小飞遇到了下面一个问题,他进行如下的解答.
(2)、【问题迁移】如图 , 已知 , ADBC,点在射线上运动,当点在 , 两点之间运动时,连接 , , , , 求与 , 之间的数量关系,并说明理由;(3)、【知识拓展】在(2)的条件下,若将“点在 , 两点之间运动”改为“点在 , 两点外侧运动点与点 , , 三点不重合”其他条件不变,请直接写出与 , 之间的数量关系.22. 【阅读思考】单元复习课后,小飞遇到了下面一个问题,他进行如下的解答.已知:如图1, , E为、之间一点,连接 , 得到.
探索、、之间的数量关系,并说明你的理由.
 (1)、小飞是这样解答的:、、之间的数量关系为 , 理由如下:
(1)、小飞是这样解答的:、、之间的数量关系为 , 理由如下:过点E作 ,
∴
∵ , ,
∴ ,
……
请接着他的思路完成解答过程.
(2)、【问题变式】如图2,若 , , 则°;(3)、【问题拓展】已知:直线 , 点A,B在直线m上,点C,D在直线n上,连接 , , 平分 , 平分 , 且 , 所在的直线交于点E.①如图3,当点B在点A的左侧时,若 , , 求的度数;
②如图4,当点B在点A的右侧时,设 , , 直接写出的度数为 ▲ (用含有 , 的式子表示).
23. 已知:点C是∠AOB的OA边上一点(点C不与点O重合),点D是∠AOB内部一点,射线CD不与OB相交.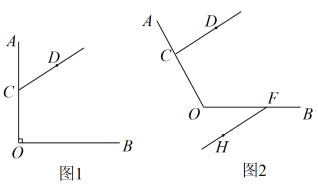 (1)、如图1,∠AOB=90°,∠OCD=120°,过点O作射线OE,使得OE//CD.(其中点E在∠AOB内部).
(1)、如图1,∠AOB=90°,∠OCD=120°,过点O作射线OE,使得OE//CD.(其中点E在∠AOB内部).①依据题意,补全图1;
②直接写出∠BOE的度数.
(2)、如图2,点F是射线OB上一点,且点F不与点O重合,当时,过点F作射线FH,使得FH//CD(其中点H在∠AOB的外部),用含的代数式表示∠OCD与∠BFH的数量关系,并证明.24. 阅读下列材料并解答问题:在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“梦想三角形”例如:一个三角形三个内角的度数分别是120°,40°,20°,这个三角形就是一个“梦想三角形”.反之,若一个三角形是“梦想三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍. (1)、如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为(2)、如图1,已知∠MON=60°,在射线OM上取一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O、B重合),若∠ACB=80°.判定△AOB、△AOC是否是“梦想三角形”,为什么?(3)、如图2,点D在△ABC的边上,连接DC,作∠ADC的平分线交AC于点E,在DC上取一点F,使得∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“梦想三角形”,求∠B的度数.
(1)、如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为(2)、如图1,已知∠MON=60°,在射线OM上取一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O、B重合),若∠ACB=80°.判定△AOB、△AOC是否是“梦想三角形”,为什么?(3)、如图2,点D在△ABC的边上,连接DC,作∠ADC的平分线交AC于点E,在DC上取一点F,使得∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“梦想三角形”,求∠B的度数.