2024年北师大版数学七(下)重难点培优训练4 必考:平行线的证明和通过变量间的图象获取信息
试卷更新日期:2024-04-13 类型:复习试卷
一、解答题
-
1. 完成下面的证明:
看图填空:已知如图,于D,于G,平分 , 求证: .
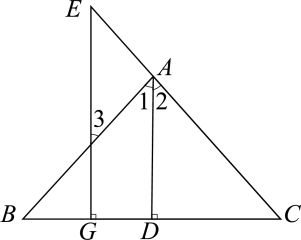
证明:∵于D,于G( ),
∴ , ( ).
∴( ).
∴( ).
∴ ▲ ( ), ▲ ( ).
又∵平分(已知),
∴( ),
∴( ).
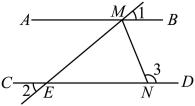
2. 完成下面的证明.如图,三角形ABC,D是边BC延长线上一点,过点C作射线CE,∠1=∠A.求证:∠A+∠B+∠ACB=180°.
证明:∵∠1=∠A,
∴AB ▲ ( ),
∴∠2= ▲ ( ).
∵∠ACB+ ▲ + ▲ =180°,
∴∠A+∠B+∠ACB=180°.
3. 完成证明并写出推理根据:如图, , , . 将求的过程填写完整.
解:已知)
▲ ( )
又(已知)
( )
▲ ( )
▲ ( )
(已知)
▲ .
4. 完成下面的解题过程.已知:如图, , 平分 , 求 .
解:∵( )
又∵
∴
∴( )
∴ ▲ ( )
∵
∴
∵平分
∴
∴ ▲ .
5. 完成下面证明.已知:如图, , , 求证: .

证明:∵(已知)
且( ),
∴(等量代换).
∴ ▲ (同位角相等,两直线平行).
∴( ).
∵(已知),
∴( ).
∴ ▲ (两直线平行,内错角相等).
∴(等量代换).
6. 请将下列证明过程补充完整:已知:如图, , 直线分别直线相交于点G,H, .
求证: .
证明:∵(已知)
( ),
∴( ),
∴ ▲ ▲ (同位角相等,两直线平行),
∴ ▲ (两直线平行,同位角相等)
又∵(已知),
∴( ),
∴(等量代换).
7. 完成证明并写出推理根据如图,已知 , 求证 ,

证明:∵(已知),
又∵ , ( )
∴ ▲ ,( )
∴ , ( )
∴ ▲ ,( )
∵ , ( )
∴ , ( )
∴ ▲ ,(同位角相等,两直线平行),
∴( )
8. 完成下面推理过程.如图:已知 , . 求证: .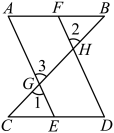
证明:(已知)
( )
( )(等量代换)
∴( )
▲ ( )
∵( )
( )
▲ ( )
( ).
9. 如图,AE平分∠BAC,∠CAE=∠CEA..求证: . 10. 如图, , 与互余, . 试说明与的位置关系,并证明你的结论.
10. 如图, , 与互余, . 试说明与的位置关系,并证明你的结论. 11. 如图, , , 求证: .
11. 如图, , , 求证: . 12. 如图,已知ABCD,射线交于点 , 交于点 , 从点引一条射线 , 若 , 求证: .
12. 如图,已知ABCD,射线交于点 , 交于点 , 从点引一条射线 , 若 , 求证: .
证明:∵ABCD(已知)
∴ ▲ (两直线平行,内错角相等)
∵(已知)
∴(等量代换)
∴BC ▲ (同旁内角互补,两直线平行)
∴ ▲ ( )
∵ ▲ (对顶角相等.)
∴(等量代换)
13. 如图,直线 , , , 求的度数.阅读下面的解答过程,并填空(理由或数学式).解:∵ (已知),

∴ (两直线平行,内错角相等)
又∵ , (已知),
∴ (等式的性质).
∴( )
∴( )
∴( )
∴
14. 中国联通在某地的资费标准为包月186元时,超出部分国内拨打0.36元/分,由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准
时间/分
1
2
3
4
5
…
电话费/元
0.36
0.72
1.08
1.44
1.8
…
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?
(2)如果用x表示超出时间,y表示超出部分的电话费,那么y与x的表达式是什么?
(3)如果打电话超出25分钟,需付多少电话费?
(4)某次打电话的费用超出部分是54元,那么小明的爸爸打电话超出几分钟?
二、综合题
-
15. 在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,如表是测得的弹簧的长度与所挂物体的质量的几组对应值:
所挂物体质量
0
1
2
3
4
弹簧长度
16
18
20
22
24
(1)、在这个表格中反映的是和两个变量之间的关系:是自变量,是因变量;(2)、弹簧长度与所挂物体质量的关系式是;(3)、若弹簧的长度为时,此时所挂重物的质量是多少?(在弹簧的允许范围内)16. 在日常生活中,我们经常要烧开水,下表是对烧水的时间与水的温度的记录:时间(分)
温度( )
根据表格中的数据解答下列问题:
(1)、第5分钟,水的温度是 ,从第分钟开始,水的温度升高到 ;(2)、从第 分钟到第 分钟,水的温度升高了多少?(3)、继续加热,请你估计在第 分钟时,水的温度是多少?随着加热时间的增加,水的温度是否会一直上升?17. 如图,反映了小明从家出发到超市购物以及从超市返回家的过程中,小明离家的距离与时间之间的关系: (1)、小明在超市购物用了分钟;(2)、小明往返途中一共用了多长时间?(3)、小明从家到超市的平均速度是多少?18. 如图所示是一位病人的体温记录图,看图回答下列问题:
(1)、小明在超市购物用了分钟;(2)、小明往返途中一共用了多长时间?(3)、小明从家到超市的平均速度是多少?18. 如图所示是一位病人的体温记录图,看图回答下列问题: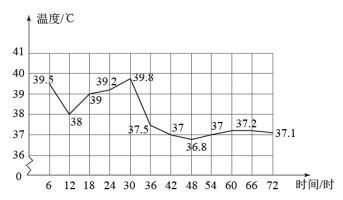 (1)、自变量是 , 因变量是 .(2)、这位病人的最高体温是摄氏度,最低体温是摄氏度.(3)、他在这天12时的体温是摄氏度.19. 小王周末骑电动车从家出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题:
(1)、自变量是 , 因变量是 .(2)、这位病人的最高体温是摄氏度,最低体温是摄氏度.(3)、他在这天12时的体温是摄氏度.19. 小王周末骑电动车从家出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题: (1)、小王在新华书店停留了多长时间?(2)、买到书后,小王从新华书店到商场的骑车速度是多少米/秒?20. 小南一家到度假村度假,小南和妈妈坐公交车先出发,爸爸自驾车沿着相同的道路后出发,爸爸到达度假村后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往度假村,(取东西的时间忽略不计),如下图是他们离家的距离()与小南离家的时间()的关系图,请根据图回答下列问题:
(1)、小王在新华书店停留了多长时间?(2)、买到书后,小王从新华书店到商场的骑车速度是多少米/秒?20. 小南一家到度假村度假,小南和妈妈坐公交车先出发,爸爸自驾车沿着相同的道路后出发,爸爸到达度假村后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往度假村,(取东西的时间忽略不计),如下图是他们离家的距离()与小南离家的时间()的关系图,请根据图回答下列问题: (1)、图中的自变量是 , 因变量是 , 小南家到该度假村的距离是(2)、小南出发小时后爸爸驾车出发,爸爸驾车的平均速度为(3)、小南从家里到度假村的路途中,当他与爸爸相遇时,离家的距离是多少?21. 小峰周末骑自行车到图书馆,他骑行一段时间后,发现钥匙丢了,于是原路返回.在等红绿灯的路口处找到了钥匙,便继续前往图书馆.小峰离家距离与所用时间的关系如图所示,请根据图中提供的信息回答下列问题:
(1)、图中的自变量是 , 因变量是 , 小南家到该度假村的距离是(2)、小南出发小时后爸爸驾车出发,爸爸驾车的平均速度为(3)、小南从家里到度假村的路途中,当他与爸爸相遇时,离家的距离是多少?21. 小峰周末骑自行车到图书馆,他骑行一段时间后,发现钥匙丢了,于是原路返回.在等红绿灯的路口处找到了钥匙,便继续前往图书馆.小峰离家距离与所用时间的关系如图所示,请根据图中提供的信息回答下列问题: (1)、图中自变量是;(2)、小峰本次去图书馆一共用了分钟;在骑行过程中最快的速度米/分;(3)、求小峰本次去图书馆骑过的所有路程和是多少米?22. 行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑行一段距离才能停止(车速不超过),对这种型号的汽车进行了测试,测得的数据如下表:
(1)、图中自变量是;(2)、小峰本次去图书馆一共用了分钟;在骑行过程中最快的速度米/分;(3)、求小峰本次去图书馆骑过的所有路程和是多少米?22. 行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑行一段距离才能停止(车速不超过),对这种型号的汽车进行了测试,测得的数据如下表:刹车时车速(km/h)
0
10
20
30
40
50
…
刹车距离(m)
0
2.5
5
7.5
10
12.5
…
(1)、自变量是 , 因变量是 .(2)、当刹车时车速为时,刹车距离是m.(3)、该种型号汽车的刹车距离用表示,刹车时车速用 , 根据上表反映的规律写出y与x之间的关系式.(4)、你能否估计一下,该种车型的汽车在车速为的行驶过程中,前面有一汽车遇紧急情况急刹并停在距该车的地方,该汽车会不会和前车追尾?请你说明理由.23. 如图,长方形中,宽 , 点P沿着四边按B→C→D→A方向运动,开始以每秒m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后恢复原速匀速运动,在运动过程中,的面积S与运动时间t的关系如图所示. (1)、直接写出长方形的长= , 长方形的宽=;(2)、直接写出 , , ;(3)、当P点运动到BC中点时,有一动点Q从点C出发,以每秒1个单位的速度沿C→D→A运动,当一个点到达终点,另一个点也停止运动,设点Q运动的时间为x秒,的面积为y,求当时,y与x之间的关系式.24. 某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)、直接写出长方形的长= , 长方形的宽=;(2)、直接写出 , , ;(3)、当P点运动到BC中点时,有一动点Q从点C出发,以每秒1个单位的速度沿C→D→A运动,当一个点到达终点,另一个点也停止运动,设点Q运动的时间为x秒,的面积为y,求当时,y与x之间的关系式.24. 某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题: (1)、图中的自变量是 , 因变量是;(2)、无人机在75米高的上空停留的时间是分钟;(3)、在上升或下降过程中,无人机的速度为米/分;(4)、图中a表示的数是;b表示的数是;(5)、图中点A表示 .25. 如图所示,小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如图反映了这个过程中,小明高家的距离y与时间x之间的对应关系.
(1)、图中的自变量是 , 因变量是;(2)、无人机在75米高的上空停留的时间是分钟;(3)、在上升或下降过程中,无人机的速度为米/分;(4)、图中a表示的数是;b表示的数是;(5)、图中点A表示 .25. 如图所示,小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如图反映了这个过程中,小明高家的距离y与时间x之间的对应关系.

根据图象回答下列问题:
(1)、食堂离小明家的距离是 , 小明从家到食堂用了分钟;(2)、小明吃早餐用了分钟,小明读报用了分钟;(3)、小明从图书馆回家的平均速度是多少?(4)、小明从家到食堂和从食堂到图书馆哪段距离走得快?26. 疫情期间,全民检测,人人有责.安安小区某时段进行核酸检测,居民有序排队入场,医务人员开始检测后,现场排队等待检测人数人与时间分钟之间的关系式为 , 用表格表示为:时间/分钟
等待检测人数人
医务人员已检测的总人数(人)与时间(分钟)之间的关系如图所示:
 (1)、如图所表示的关系中,自变量是 , 因变量;(2)、图中点表示的含义是 ;(3)、关系式中,的值为 ;(4)、医务人员开始检测 分钟后,现场排队等待检测人数与医务人员已检测的总人数相同;(5)、如果该小区共有居民人,那么医务人员全部检测完该小区居民共需 分钟.27. 如图,是反映一辆出租车从甲地到乙地的速度与时间的关系图;根据图形,回答下列问题:
(1)、如图所表示的关系中,自变量是 , 因变量;(2)、图中点表示的含义是 ;(3)、关系式中,的值为 ;(4)、医务人员开始检测 分钟后,现场排队等待检测人数与医务人员已检测的总人数相同;(5)、如果该小区共有居民人,那么医务人员全部检测完该小区居民共需 分钟.27. 如图,是反映一辆出租车从甲地到乙地的速度与时间的关系图;根据图形,回答下列问题: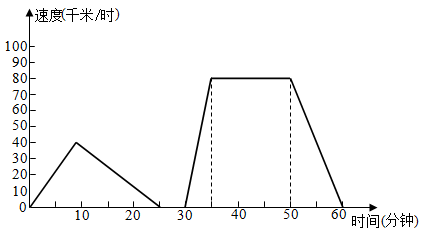 (1)、在这个变化过程中,自变量是什么?因变量是什么?(2)、汽车从出发到最后停止共经过了多长时间?它的最高时速是多少?(3)、汽车在哪段时间保持匀速行驶?速度是多少?28. 如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答:
(1)、在这个变化过程中,自变量是什么?因变量是什么?(2)、汽车从出发到最后停止共经过了多长时间?它的最高时速是多少?(3)、汽车在哪段时间保持匀速行驶?速度是多少?28. 如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答: (1)、甲的出发时间是点.(2)、到十点时,乙大约走了千米.(3)、到十点为止,(甲、乙)的速度快.(4)、两人最终相遇时间是点.(5)、你能将图象中得到信息,编个故事吗?29. 如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度与碗的数量的关系如下表:
(1)、甲的出发时间是点.(2)、到十点时,乙大约走了千米.(3)、到十点为止,(甲、乙)的速度快.(4)、两人最终相遇时间是点.(5)、你能将图象中得到信息,编个故事吗?29. 如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度与碗的数量的关系如下表:碗的数量(个)
2
3
4
...
高度()
...
 (1)、上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、若把6个这样的碗整齐地叠放在水平桌面上时,这摞碗的高度是多少?(3)、用x(个)表示这摞碗的数量,用y(cm)表示这摞碗的高度,请表示出y与x的关系式;(4)、这摞碗的高度是否可以为 , 如果可以,求这摞碗的数量;如果不可以,请说明理由.30. 如图①,在中,是三角形的高,且 , E是一个动点,从点B向终点C运动,其速度与时间的变化关系如图②所示,已知 .
(1)、上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、若把6个这样的碗整齐地叠放在水平桌面上时,这摞碗的高度是多少?(3)、用x(个)表示这摞碗的数量,用y(cm)表示这摞碗的高度,请表示出y与x的关系式;(4)、这摞碗的高度是否可以为 , 如果可以,求这摞碗的数量;如果不可以,请说明理由.30. 如图①,在中,是三角形的高,且 , E是一个动点,从点B向终点C运动,其速度与时间的变化关系如图②所示,已知 . (1)、在点E的运动过程中,求的面积与运动时间之间的关系式;(2)、当点E运动停止后,求的面积.
(1)、在点E的运动过程中,求的面积与运动时间之间的关系式;(2)、当点E运动停止后,求的面积.