2023-2024学年广东省七年级下学期数学期中仿真模拟卷四【范围:人教版第5-7章】
试卷更新日期:2024-04-13 类型:期中考试
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 在平面直角坐标系中,点P( , 2)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 以下命题为真命题的是( )A、同位角相等 B、相等的角是对顶角 C、过直线外一点有且只有一条直线与已知直线平行 D、两直线平行,同旁内角相等3. 如图,已知 AB∥CD,下列结论中,正确的是( )
 A、∠1=∠2 B、∠2=∠3 C、∠1=∠4 D、∠3=∠44. 一个正方体的水晶砖,体积为100cm3 , 它的棱长大约在( )A、4cm~5cm之间 B、5cm~6cm之间 C、6cm~7cm之间 D、7cm~8cm之间5. 下列各式中正确的是( )A、 B、 C、 D、6. 实数: , , . , , 每两个之间增加一个 , 中,无理数有( )A、个 B、个 C、个 D、个7. 下列图形中,能说明“相等的角是对顶角”为假命题的是( )A、
A、∠1=∠2 B、∠2=∠3 C、∠1=∠4 D、∠3=∠44. 一个正方体的水晶砖,体积为100cm3 , 它的棱长大约在( )A、4cm~5cm之间 B、5cm~6cm之间 C、6cm~7cm之间 D、7cm~8cm之间5. 下列各式中正确的是( )A、 B、 C、 D、6. 实数: , , . , , 每两个之间增加一个 , 中,无理数有( )A、个 B、个 C、个 D、个7. 下列图形中,能说明“相等的角是对顶角”为假命题的是( )A、 B、
B、 C、
C、 D、
D、 8. 已知两个不相等的实数x , y满足: , , 则的值为( )A、 B、0 C、1 D、9. 如图,在平面直角坐标系中, , , , , 一只电子蚂蚁从点A出发按的规律每秒1个单位长度爬行,则2023秒时蚂蚁所在的位置是( )
8. 已知两个不相等的实数x , y满足: , , 则的值为( )A、 B、0 C、1 D、9. 如图,在平面直角坐标系中, , , , , 一只电子蚂蚁从点A出发按的规律每秒1个单位长度爬行,则2023秒时蚂蚁所在的位置是( )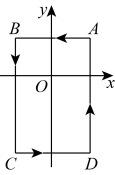 A、 B、 C、 D、10. 如图1,当光从空气进入水中时,会发生折射,满足入射角∠1 与折射角∠2 的度数比为4:3.如图2,在同一平面上,两条光线同时从空气进入水中,两条入射光线与水面的夹角分别为α,β,水中两条折射光线的夹角为γ,则α,β,γ三者之间的数量关系为( )
A、 B、 C、 D、10. 如图1,当光从空气进入水中时,会发生折射,满足入射角∠1 与折射角∠2 的度数比为4:3.如图2,在同一平面上,两条光线同时从空气进入水中,两条入射光线与水面的夹角分别为α,β,水中两条折射光线的夹角为γ,则α,β,γ三者之间的数量关系为( )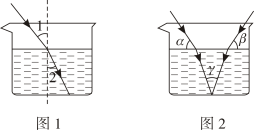 A、 B、 C、α+β=γ D、
A、 B、 C、α+β=γ D、二、填空题
-
11. 我们规定向东和向北方向为正,如向东走4米,向北走走6米,记为(4,6),则向西走5米,向北走3米,记为;12. 若一个正数m的两个平方根分别是3a+2和a-10,则m的值为 .13. 象棋作为中国传统棋类益智游戏,用具简单,趣味性强,深受大众喜爱,其“马走日,相走田,小卒一去不会返……”的口诀也被很多人熟知.如图,是一盘象棋的一部分,在象棋棋盘上建立平面直角坐标系,象棋中小正方形的边长视为一个单位长度,若“马”的坐标 , “相”的坐标为 , 则“炮”的坐标为 .
 14. 将一副直角三角尺按如图所示的方式叠放在一起,若AC∥DE,则∠DAB的度数为
14. 将一副直角三角尺按如图所示的方式叠放在一起,若AC∥DE,则∠DAB的度数为 15. 如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2018的坐标为.
15. 如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2018的坐标为.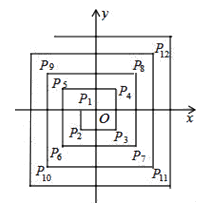
三、解答题(共8题,共75分)
-
16. 计算:(1)、;(2)、 .17. 王老师给同学们布置了这样一道习题:一个正数的算术平方根为 , 它的平方根为 , 求这个正数.
小达的解法如下:依题意可知:解得:则: , 所以这个正数为 .
王老师看后说,小达的解法不完整,请同学们给出这道习题完整的解法.
18. 求下列各式中的x:(1)、;(2)、 .19. 已知点 , 解答下列各题:(1)、若点P在x轴上,则点P的坐标为 ;(2)、若 , 且轴,则点P的坐标为 ;(3)、若点P在第二象限,且它到x轴、y轴的距离相等,求的值.20. 看图填空,在括号内填写理由.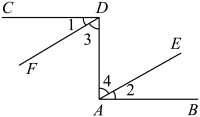
如图,已知 . 试说明 .
证明:(已知),
, ( ),
, ,
又(已知),
( ),
( ).
21. 如图,在平面直角坐标系中, , , . (1)、过点作 , 且点在格点上,则点的坐标是;(2)、经平移后对应点为 , 将作同样的平移得到 , 在图中画出;22. 如图,线段交线段 , 于点H,G,已知 , ,
(1)、过点作 , 且点在格点上,则点的坐标是;(2)、经平移后对应点为 , 将作同样的平移得到 , 在图中画出;22. 如图,线段交线段 , 于点H,G,已知 , ,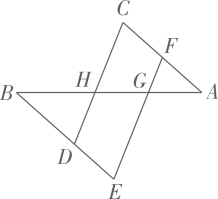 (1)、求证: .(2)、若 , 求证: .(3)、在(2)的条件下,若 , 求的度数.23. 如图所示, 轴于点A , 点B的坐标为 ,将线段BA沿x轴方向平移6个单位,平移后的线段为CD .
(1)、求证: .(2)、若 , 求证: .(3)、在(2)的条件下,若 , 求的度数.23. 如图所示, 轴于点A , 点B的坐标为 ,将线段BA沿x轴方向平移6个单位,平移后的线段为CD .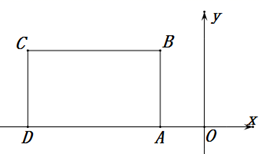 (1)、点C的坐标为;线段BC与线段AD的位置关系是;(2)、在四边形 中,点P从点A出发,沿“ ”移动,移动到点D停止.若点P的速度为每秒1个单位长度,设运动时间为t秒,回答下列问题:
(1)、点C的坐标为;线段BC与线段AD的位置关系是;(2)、在四边形 中,点P从点A出发,沿“ ”移动,移动到点D停止.若点P的速度为每秒1个单位长度,设运动时间为t秒,回答下列问题:①当点P在线段AB上运动时,若三角形ADP的面积为 ,则此时 .
②当点P在线段BC上运动时,直接写出点P在运动过程中的坐标为()(用含t的式子表示);
③在②的情况下,当四边形 的面积是四边形 面积的 时,点P的横坐标为 .