北师大版数学中考仿真模拟试题(四)
试卷更新日期:2024-04-13 类型:中考模拟
一、选择题(每题4分,共40分)
-
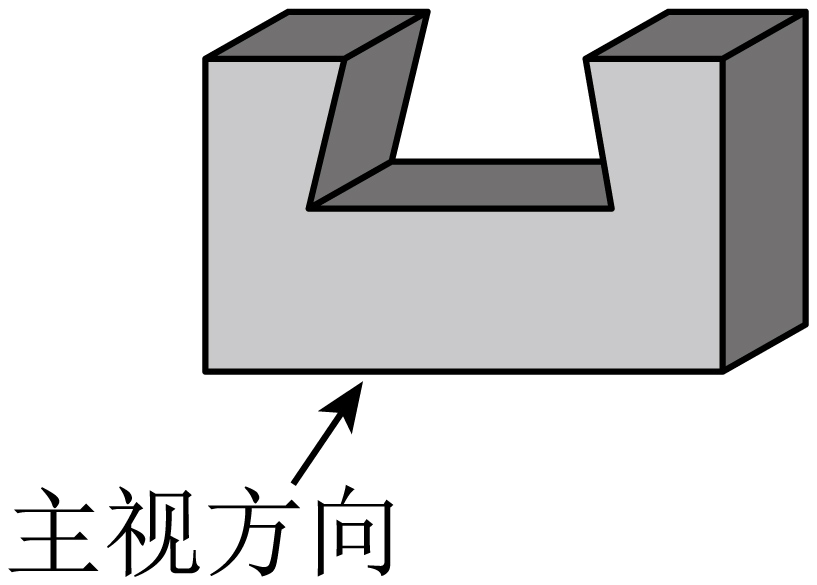
1. 的绝对值是( )A、 B、 C、 D、2. 2022年我国粮食总产量再创新高,达686530000吨.将数字686530000用科学记数法表示为( )A、 B、 C、 D、3. 榫卯是古代中国建筑、家具及其它器械的主要结构方式,是我国工艺文化精神的传奇;凸出部分叫榫,凹进部分叫卯,下图是某个部件“卯”的实物图,它的主视图是( )
 A、
A、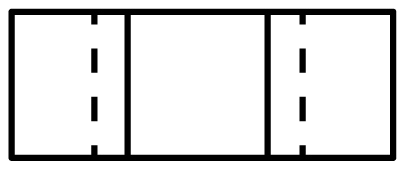 B、
B、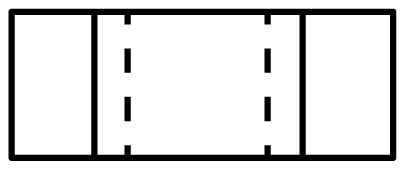 C、
C、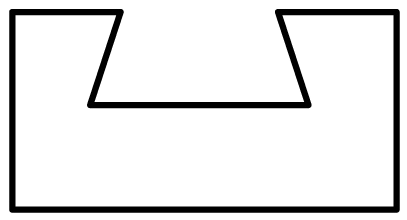 D、
D、 4. 下列运算结果正确的是( )A、 B、 C、 D、5. 如图,在矩形中,对角线与相交于点 , , , 垂足为点 , 是的中点,连接 , 若 , 则矩形的周长是( )
4. 下列运算结果正确的是( )A、 B、 C、 D、5. 如图,在矩形中,对角线与相交于点 , , , 垂足为点 , 是的中点,连接 , 若 , 则矩形的周长是( )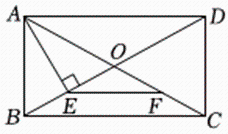 A、 B、 C、 D、6. 若x=3是关于x的一元二次方程的一个根,下面对a的值估计正确的是( )A、<a<1 B、1<a< C、<a<2 D、2<a<7. 某校拟派一名跳高运动员参加一项校际比赛,对名跳高运动员进行了多次选拔比赛,他们比赛成绩的平均数和方差如下表:
A、 B、 C、 D、6. 若x=3是关于x的一元二次方程的一个根,下面对a的值估计正确的是( )A、<a<1 B、1<a< C、<a<2 D、2<a<7. 某校拟派一名跳高运动员参加一项校际比赛,对名跳高运动员进行了多次选拔比赛,他们比赛成绩的平均数和方差如下表:甲
乙
丙
丁
平均数
方差
根据表中数据,要从中选择一名平均成绩好,且发挥稳定的运动员参加比赛,最合适的人选是( )
A、甲 B、乙 C、丙 D、丁8. 在项目化学习中,“水是生命之源”项目组为了解本地区人均淡水消耗量,需要从四名同学(两名男生,两名女生)中随机抽取两人,组成调查小组进行社会调查,恰好抽到一名男生和一名女生的概率是( )A、 B、 C、 D、9. 在同一平面直角坐标系中,函数和为常数,的图象可能是( )A、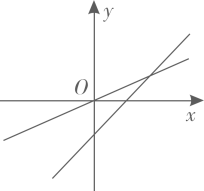 B、
B、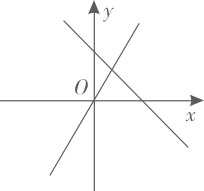 C、
C、 D、
D、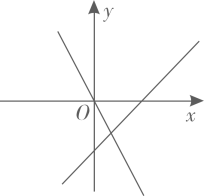 10. 如图,二次函数图象的一部分与x轴的一个交点坐标为 , 对称轴为直线 , 结合图象给出下列结论:
10. 如图,二次函数图象的一部分与x轴的一个交点坐标为 , 对称轴为直线 , 结合图象给出下列结论: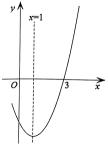
①;②;③;
④关于x的一元二次方程有两个不相等的实数根;
⑤若点 , 均在该二次函数图象上,则.其中正确结论的个数是( )
A、4 B、3 C、2 D、1二、填空题(每题4分,共24分)
-
11. 若式子 在实数范围内有意义,则x的取值范围是 .12. 如图,在中, . P为边上一动点,作于点D,于点E,则的最小值为 .
 13. 某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是元.
13. 某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是元. 14. 如图,是边长为6的等边三角形,点在边上,若 , , 则 .
14. 如图,是边长为6的等边三角形,点在边上,若 , , 则 .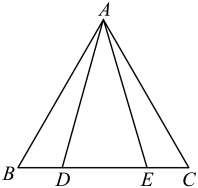 15. 如图,在直角中, , , 将绕点顺时针旋转至的位置,点是的中点,且点在反比例函数的图象上,则的值为 .
15. 如图,在直角中, , , 将绕点顺时针旋转至的位置,点是的中点,且点在反比例函数的图象上,则的值为 . 16. 如图,在边长为2的正方形中,E,F分别是上的动点,M,N分别是的中点,则的最大值为 .
16. 如图,在边长为2的正方形中,E,F分别是上的动点,M,N分别是的中点,则的最大值为 .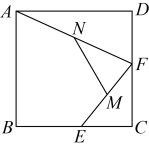
三、解答题(共9题,共86分)
-
17. 计算 .18. 先化简,再求值:
,其中 , .
19. “春节”是我国的传统佳节,民间历来有吃“饺子”的习俗我市某食品厂为了解市民对去年销量较好的猪肉馅饺、牛肉馅饺、虾肉馅饺、素馅饺以下分别用、、、表示这四种不同口味饺子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图尚不完整 .
请根据以上信息回答
(1)、本次参加抽样调查的居民有人;(2)、将两幅不完整的图补充完整;(3)、若居民区有人,请估计爱吃饺的人数;(4)、若有外型完全相同的、、、饺子各一个,煮熟后,小王吃了两个用列表或画树状图的方法,求他吃到饺的概率.20. 在中,是斜边上的高.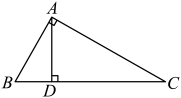 (1)、证明:;(2)、若 , 求的长.21. 如图,过原点O的直线与反比例函数(k≠0)的图象交于A(1,2),B两点,一次函数y2=mx+b(m≠0)的图象过点A与反比例函数交于另一点C(2,n).
(1)、证明:;(2)、若 , 求的长.21. 如图,过原点O的直线与反比例函数(k≠0)的图象交于A(1,2),B两点,一次函数y2=mx+b(m≠0)的图象过点A与反比例函数交于另一点C(2,n).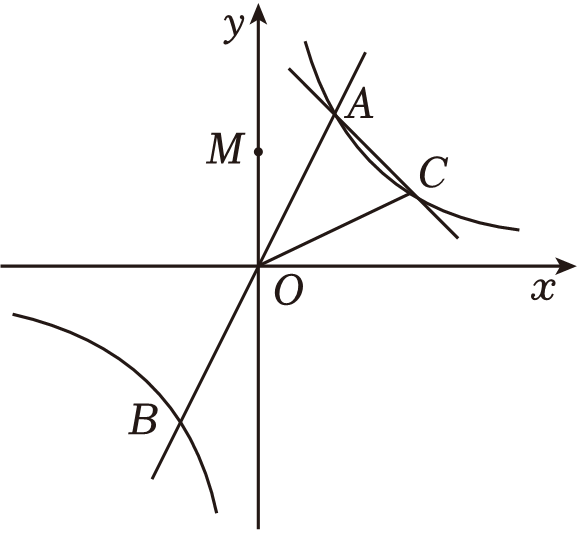 (1)、求反比例函数的解析式;当y1>y2时,根据图象直接写出x的取值范围;(2)、在y轴上是否存在点M,使得△COM为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.22. 为积极响应州政府“悦享成长·书香恩施”的号召,学校组织150名学生参加朗诵比赛,因活动需要,计划给每个学生购买一套服装.经市场调查得知,购买1套男装和1套女装共需220元;购买6套男装与购买5套女装的费用相同.(1)、男装、女装的单价各是多少?(2)、如果参加活动的男生人数不超过女生人数的 , 购买服装的总费用不超过17000元,那么学校有几种购买方案?怎样购买才能使费用最低,最低费用是多少?23. 已知在中, , , , 以边为直径作 , 与边交于点 , 点为边的中点,连接 .
(1)、求反比例函数的解析式;当y1>y2时,根据图象直接写出x的取值范围;(2)、在y轴上是否存在点M,使得△COM为等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.22. 为积极响应州政府“悦享成长·书香恩施”的号召,学校组织150名学生参加朗诵比赛,因活动需要,计划给每个学生购买一套服装.经市场调查得知,购买1套男装和1套女装共需220元;购买6套男装与购买5套女装的费用相同.(1)、男装、女装的单价各是多少?(2)、如果参加活动的男生人数不超过女生人数的 , 购买服装的总费用不超过17000元,那么学校有几种购买方案?怎样购买才能使费用最低,最低费用是多少?23. 已知在中, , , , 以边为直径作 , 与边交于点 , 点为边的中点,连接 .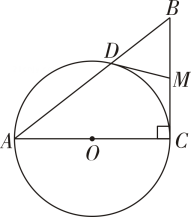 (1)、求证:是的切线;(2)、点为直线上任意一动点,连接交于点 , 连接 .
(1)、求证:是的切线;(2)、点为直线上任意一动点,连接交于点 , 连接 .当时,求的长;
求的最大值.
24. 如图,一条抛物线经过的三个顶点,其中为坐标原点,点 , 点在第一象限内,对称轴是直线 , 且的面积为18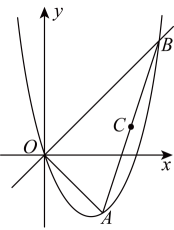 (1)、求该抛物线对应的函数表达式;(2)、求点的坐标;(3)、设为线段的中点,为直线上的一个动点,连接 , , 将沿翻折,点的对应点为 . 问是否存在点 , 使得以 , , , 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点的坐标;若不存在,请说明理由.25. 【发现】如图1,有一张三角形纸片 , 小宏做如下操作:
(1)、求该抛物线对应的函数表达式;(2)、求点的坐标;(3)、设为线段的中点,为直线上的一个动点,连接 , , 将沿翻折,点的对应点为 . 问是否存在点 , 使得以 , , , 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点的坐标;若不存在,请说明理由.25. 【发现】如图1,有一张三角形纸片 , 小宏做如下操作: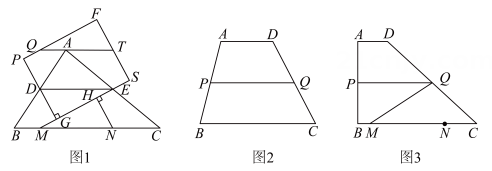
⑴取 ,
 中点D,E,在边上作;
中点D,E,在边上作;⑵连接 , 分别过点D,N作 , , 垂足为G,H;
⑶将四边形剪下,绕点D旋转至四边形的位置,将四边形剪下,绕点E旋转至四边形的位置;
⑷延长 , 交于点F.
小宏发现并证明了以下几个结论是正确的:
①点Q,A,T
 一条直线上;
一条直线上;②四边形是矩形;
③;
④四边形与的面积相等.
(1)、【任务1】请你对结论①进行证明.(2)、【任务2】如图2,在四边形中, , P,Q分别是 , 的中点,连接 . 求证: .(3)、【任务3】如图3,有一张四边形纸 , , , , , , 小丽分别取 , 的中点P,Q,在边上作 , 连接 , 她仿照小宏的操作,将四边形分割、拼成了矩形.若她拼成的矩形恰好是正方形,求的长.