2023-2024学年广东省七年级下学期数学期中仿真模拟卷三【范围:人教版第5-7章】
试卷更新日期:2024-04-13 类型:期中考试
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 下列各数中的无理数是( )A、 B、 C、0 D、2. 下列各式成立的是( )A、 B、 C、 D、3. 下列说法正确的个数( )
①过一点有且只有一条直线与已知直线垂直;②平面内,互相垂直的两条直线一定相交;③有公共顶点且相等的角是对顶角;④直线外一点到已知直线的垂线段,叫做这点到直线的距离;⑤过一点有且只有一条直线与已知直线平行.
A、0个 B、1个 C、2个 D、3个4. 若点P(x,y)在第四象限,且|x|=2,|y|=3,则x+y=( )A、﹣1 B、1 C、5 D、﹣55. 下列说法错误的是( )A、的立方根是 B、算术平方根等于本身的数是 , C、 D、的平方根是6. 若与的两边分別平行,且 , 则的度数为( )A、 B、 C、或 D、或7. 按如图所示的程序计算,若开始输入的x的值是64,则输出的y的值是( ) A、 B、 C、2 D、38. 如图,E在线段的延长线上, , , , 连交于G,的余角比大 , K为线段上一点,连 , 使 , 在内部有射线 , 平分 . 则下列结论:①;②平分;③;④ . 其中正确结论的个数有( )
A、 B、 C、2 D、38. 如图,E在线段的延长线上, , , , 连交于G,的余角比大 , K为线段上一点,连 , 使 , 在内部有射线 , 平分 . 则下列结论:①;②平分;③;④ . 其中正确结论的个数有( )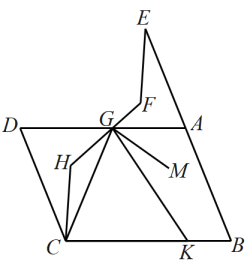 A、1个 B、2个 C、3个 D、4个9. 下列说法:;数轴上的点与实数成一一对应关系;是的平方根;任何实数不是有理数就是无理数;两个无理数的和还是无理数;无理数都是无限小数,正确的个数有( )A、个 B、个 C、个 D、个10. 如图,已知 , , 点是射线上一动点(与点不重合),、分别平分和 , 分别交射线于点、 , 下列结论:①;②;③当时,;④当点运动时,的数量关系不变.其中正确结论有( )个.
A、1个 B、2个 C、3个 D、4个9. 下列说法:;数轴上的点与实数成一一对应关系;是的平方根;任何实数不是有理数就是无理数;两个无理数的和还是无理数;无理数都是无限小数,正确的个数有( )A、个 B、个 C、个 D、个10. 如图,已知 , , 点是射线上一动点(与点不重合),、分别平分和 , 分别交射线于点、 , 下列结论:①;②;③当时,;④当点运动时,的数量关系不变.其中正确结论有( )个.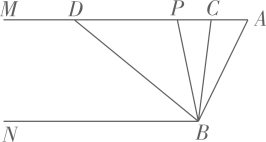 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题:本大题共5小题,每小题3分,共15分.
-
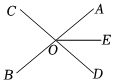
11. 已知 , , 则 .12. 长方形ABCD的边AB=5,BC=7,若将该长方形放在平面直角坐标系中,使点A的坐标为(-1,2)且AB∥x轴,BC∥y轴,C不在第三象限,则C点的坐标是 .13. 如图,直线、相交于点 , 平分 , 若 , 则的度数是 .
 14. 已知 , 则;15. 规定符号[a]表示实数a的整数部分,[]=0,[4.15]=4.按此规定[+2]的值为 .
14. 已知 , 则;15. 规定符号[a]表示实数a的整数部分,[]=0,[4.15]=4.按此规定[+2]的值为 .三、解答题(共8题,共75分)
-
16. 计算: .17. 计算:;18. 已知:如图, , , , , 求证: .
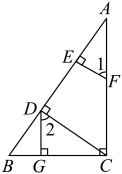
证明:∵ , (已知)
∴ , (垂直定义)
∴
∴( )
∴ ▲ ( )
∵(已知)
∴ ▲ (等量代换)
∴( )
∴ ▲ ( )
∵(已知)
∴(垂直定义)
∴ ▲ (等量代换)
∴(垂直定义)
19. 如图,在平面直角坐标系中,三角形三个顶点的坐标分别为 , , . 若三角形ABC中任意一点 , 平移后对应点为 , 将三角形作同样的平移得到三角形 , 点A,B,C的对应点分别为 , , . (1)、在图中画出平移后的三角形;(2)、三角形的面积为;(3)、点Q为y轴上一动点,当三角形的面积是3时,直接写出点Q的坐标.20. 如图,点F 在线段AB上,点E,G在线段CD 上,FG∥AE,∠1=∠2.
(1)、在图中画出平移后的三角形;(2)、三角形的面积为;(3)、点Q为y轴上一动点,当三角形的面积是3时,直接写出点Q的坐标.20. 如图,点F 在线段AB上,点E,G在线段CD 上,FG∥AE,∠1=∠2.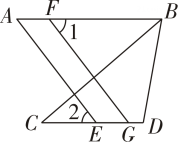 (1)、试说明:AB∥CD.(2)、若BC平分∠ABD,∠D=112°,求∠C的度数.21. 如图,点在直线上, , .
(1)、试说明:AB∥CD.(2)、若BC平分∠ABD,∠D=112°,求∠C的度数.21. 如图,点在直线上, , .求证: .
 22. 如图1,已知AB∥CD,∠ACD的平分线交AB交于点E.
22. 如图1,已知AB∥CD,∠ACD的平分线交AB交于点E. (1)、求证:∠ACE=∠AEC;(2)、如图2,当点F在线段CE上时,连接FA.过点F作FM∥AE交AC于点M,当∠ACD=130°,且∠FAB=25°时,求∠AFC的度数;(3)、如图1,若点F为射线CE上一点.连接FA,探究∠FCD、∠FAB和∠AFC之间的数量关系,并证明你的结论.23. 据说我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求出它的立方根.华罗庚脱口而出:39.邻座的乘客十分惊奇,忙问计算的奥妙,华罗庚讲述了计算过程:
(1)、求证:∠ACE=∠AEC;(2)、如图2,当点F在线段CE上时,连接FA.过点F作FM∥AE交AC于点M,当∠ACD=130°,且∠FAB=25°时,求∠AFC的度数;(3)、如图1,若点F为射线CE上一点.连接FA,探究∠FCD、∠FAB和∠AFC之间的数量关系,并证明你的结论.23. 据说我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求出它的立方根.华罗庚脱口而出:39.邻座的乘客十分惊奇,忙问计算的奥妙,华罗庚讲述了计算过程:第一步:因为 , , , 所以 .
第二步:因为59319的个位上的数是9,只有个位数字是9的数的立方的个位数字是9,所以的个位数字是9.
第三步:如果划去59319后面的三位319得到数59,而 , , 所以 ,
所以 , 即的十位数字是3.
所以 .
请根据上述材料解答下列问题:
(1)、用上述方法确定4913的立方根的个位数字是 .(2)、用上述方法确定50653的立方根是 .(3)、求的值,要求写出计算过程.