2023-2024学年广东省深圳市七年级下学期数学期中仿真模拟卷一【范围：1-3章】

试卷更新日期：2024-04-13 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分，每小题有四个选项，只有一个是正确的）

1. $3^{2} \times 3^{7}$ 的值是（）

A、 $3^{9}$ B、 $3^{14}$ C、 $3^{5}$ D、 $3^{11}$

查看试题解析
2. 蚕丝是大自然中的天然纤维，是中国古代文明产物之一，也成为散发着现代科学技术魅力的新材料 $.$ 某蚕丝的直径大约是 $0.000016$ 米， $0.000016$ 用科学记数法表示为（）

A、 $0.16 \times 1 0^{- 4}$ B、 $1.6 \times 1 0^{- 4}$ C、 $1.6 \times 1 0^{- 5}$ D、 $16 \times 1 0^{- 4}$

查看试题解析
3. 下面四个图形中， $∠ 1 = ∠ 2$ 一定成立的是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、 $a^{4} \cdot a^{7} = a^{28}$ B、 ${(a^{3})}^{3} = a^{9}$ C、 ${(a^{3} b^{2})}^{3} = a^{6} b^{5}$ D、 $b^{2} + b^{2} = b^{4}$

查看试题解析
5. 下列图形中，由 $A B ∥ C D$ ，能得到 $∠ 1 = ∠ 2$ 的是（）

A、 B、 C、 D、

查看试题解析
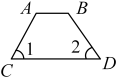6. 下列各式中，不能用平方差公式计算的是（）

A、 $(- x - y) (x - y)$ B、 $(- x + y) (- x - y)$ C、 $(x + y) (- x + y)$ D、 $(x - y) (- x + y)$

查看试题解析
7. 若 $4 x^{2} + p x y + \frac{1}{16} y^{2}$ 是完全平方式，则 p的值为（）

A、1 B、±2 C、±1 D、±4

查看试题解析
8. 如图，直线 $a$ ， $b$ 被直线 $c$ 所截， $a / / b$ ， $∠ 1 = ∠ 2$ ，若 $∠ 3 = 40 °$ ，则 $∠ 4$ 等于（）

A、 $40 °$ B、 $50 °$ C、 $70 °$ D、 $80 °$

查看试题解析
9. 【观察】① $(x - 1) (x + 1) = x^{2} - 1$ ；
② $(x - 1) (x^{2} + x + 1) = x^{3} - 1$ ；

③ $(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$ ；

……

【归纳】由此可得： $(x - 1) (x^{n} + x^{n - 1} + x^{n - 2} + \dots + x + 1) = x^{n + 1} - 1$ ；

【应用】请运用上面的结论，计算： $2^{2023} + 2^{2022} + 2^{2021} + \dots + 2^{2} + 2 + 1 =$ （）

A、 $2^{2023} - 1$ B、 $2^{2024} - 1$ C、 $2^{2024}$ D、 $2^{2025} - 1$

查看试题解析
10. 如图，已知，∠BAC=∠ACD=90°，∠ABC=∠ADC，CE⊥AD．有下列结论：①AD∥BC；②∠ECD=∠DAC；③∠CEF=∠CFE；④CACE=∠ABC．其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本题有5小题，每小题3分，共15分）

11. 老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下： $\times 2 x = 4 x^{2} - 6 x y + 2 x$ ，则所指的多项式为．

查看试题解析
12. 若一个角的补角比这个角的余角的3倍大10°，则这个角为度．

查看试题解析
13. 已知8•（2^m）ⁿ＝64，|n|＝1，则m＝．

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ A = 100 °$ ， $△ A B C$ 的角平分线 $B D$ ， $C E$ 交于点 $O$ ，则 $∠ B O C =$ ．

查看试题解析
15. 如图是某灯具的镜面反射示意图，从光源点 $P$ 处发出的光线 $P A$ ， $P B$ 经弯曲的镜面反射后射出，且满足反射光线 $A C ∥ B D$ ，若 $∠ P A C = 40 °$ ， $P A ⊥ P B$ 于点 $P$ ，则 $∠ P B D$ 的度数为．

查看试题解析

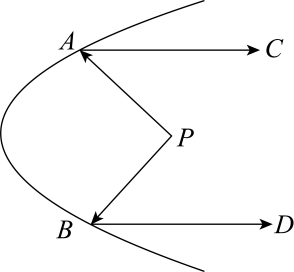
三、解答题(本题共7小题，共55分)

16. 计算：

(1)、 $(3.14 - π)^{0} + | - 2 | - {(\frac{1}{2})}^{- 1}$ ；

(2)、 $202 0^{2} - 2019 \times 2021$ ．（要求用公式简便计算）

查看试题解析
17. 化简求值：
[（x+2y）²﹣（x﹣2y）²﹣（x+2y）（x﹣2y）﹣4y²]÷2x，其中x=﹣2，y= $\frac{1}{2}$ ．

查看试题解析
18. 已知：∠ $α$ ．请你用直尺和圆规画一个∠BAC，使∠BAC=∠ $α$ ．（要求：要保留作图痕迹．）

查看试题解析
19. 填空并完成以下证明：
已知，如图， $∠ 1 = ∠ A C B$ ， $∠ 2 = ∠ 3$ ， $F H ⊥ A B$ 于 $H$ ，求证： $C D ⊥ A B$ ．

证明： $F H ⊥ A B ($ 已知 $)$

$∴ ∠ B H F =$                      ．

$∵ ∠ 1 = ∠ A C B ($ 已知 $)$

$∴ D E / / B C$ （）

$∴ ∠ 2 =$                       .（）

$∵ ∠ 2 = ∠ 3 ($ 已知 $)$

$∴ ∠ 3 =$                         .（）

$∴ C D / / F H$ （）

$∴ ∠ B D C = ∠ B H F =$                     $°$ .（）

$∴ C D ⊥ A B$ ．

查看试题解析
20. 如图，是由四个长为 $m$ ，宽为 $n$ 的小长方形拼成的正方形．

(1)、图中的阴影正方形的边长可表示为 $($ 用含 $m$ ， $n$ 的代数式表示 $)$ ；

(2)、根据图形中的数量关系，请你结合图形直接写出 $(m + n)^{2}$ ， $(m - n)^{2}$ ， $m n$ 之间的一个等量关系；

(3)、根据(2)中的结论，解决下列问题：若 $m + n = 7$ ， $m n = 3$ ，求阴影正方形的面积．

查看试题解析
21. 佳佳和萌萌一起参加中长跑，起跑后路程 $S (m)$ 与时间 $t (m i n)$ 之间的关系如图所示．

(1)、在上述关系中，自变量是，因变量是；

(2)、这次比赛的路程是m；

(3)、萌萌将本次中长跑分起跑、途中跑和冲刺跑三阶段，经历了两次变速，在第 $m i n$ 速度最慢，速度为 $m / m i n$ ；

(4)、通过计算说明萌萌与佳佳何时相遇．

查看试题解析
22. 【概念认识】
两条直线相交所形成的锐角或直角称为这两条直线的夹角，如果两条直线的夹角为α，那么我们称这两条直线是“α相交线”例如；如图①，直线m和直线n为“α相交线”我们已经知道两条平行线被第三条直线所截，同位角相等、内错角相等、同旁内角互补，那么若两条直线为“α相交线”，它们被第三条直线所截后形成的同位角、内错角、同旁内角之间有什么关系呢？

(1)、【初步研究】
如图②，直线m与直线n是“α相交线”，求证： $∠ 1 - ∠ 2 = α$
小明的证法如图③．若直线m与直线n交于点O，
直线m与直线n是“α相交线”．
∵ $∠ A O B = α$ ．
∴ $∠ 1$ 是 $△ A B O$ 的外角，
∴ $∠ 1 = ∠ 2 + ∠ A O B$ ．
即 $∠ 1 - ∠ 2 = α$ ．
请补充完整小明的证明过程，并用另一种不同的方法进行证明

(2)、【深入思考】
如图④，直线m与直线n是α相交线，
①找出直线m与直线n被直线l所截得的内错角，并直接写出内错角与α的关系；
②找出直线m与直线n被直线l所截得的同旁内角，并直接写出每对同旁内角与α的关系；

(3)、【综合运用】
如图⑤，已知∠α，用直尺和圆规按下列要求作图，
如图⑥，直线 $A B$ 外求作一点M，使得直线 $M A$ 与直线 $M B$ 是“α相交线”（不写作图过程，保留作图痕迹）．

查看试题解析